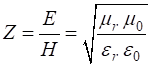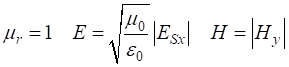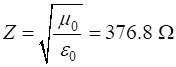DOING PHYSICS WITH MATLAB

 

[1D] FDTD electromagnetic wave simulations propagating in non-magnetic and uniform dielectric media

Ian Cooper

Please email any corrections, comments, suggestions or additions

 matlabvisualphysics@gmail.com

Matlab Download Directory

 

ft_03.m

Download and run the script ft_03.m. Carefully inspect the script to see how the FDTD method is implemented.  Many variables can be changed throughout the script, for example, type of excitation signal, boundary conditions, time scales, properties of the media.

 

View  ELECTROMAGNETISM USING THE FDTD METHOD

 

 

Simulation 1     Free Space Propagation

    Nz = 400                       Number of grid points for Z space

    flagS = 1                        Pulse

    zS = 20                          Source: Z location

    A = 1                              Amplitude

   width = 25                     Width of pulse

   centre = 100                 Time step for center of pulse

   flagBC = 1                      Absorbing boundary conditions

   M2 = round(Nz/2)       Index for start of Medium 2

   eR1 =1   S1 = 0             Relative permittivity & conductivity Medium 1

   eR2 = 1  S2 = 0             Relative permittivity  & conductivity Medium 2

 

Note: The absorbing boundary conditions only apply to the case for the propagation of the wave in free space ( ).

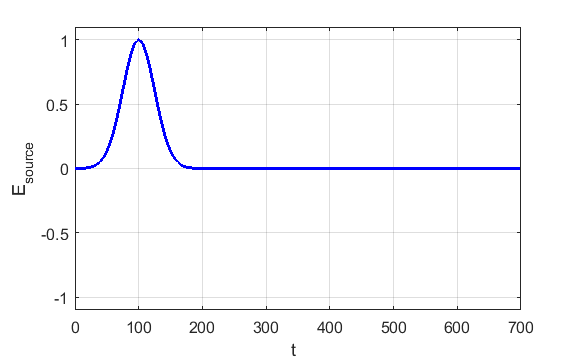
Fig.1     Gaussian source. A “hard source” is used because a specific value is imposed on the FDTD grid. However, the value of Ex at the source point added to the source gives a “soft source”. With a hard source, a propagating pulse will see the value and be reflected, because a hard value of Ex looks like a metal wall to FDTD. With a soft source, a propagating will just pass straight through.

                        Ex(ct,zS) = source(ct)                                     hard source

                        Ex(ct,zS) = Ex(ct,Zs) + source(CT)                 soft source

 

 

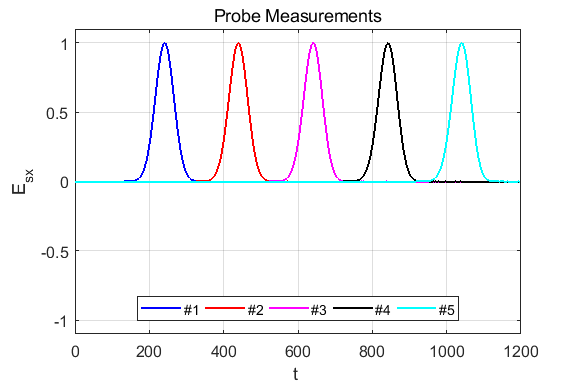
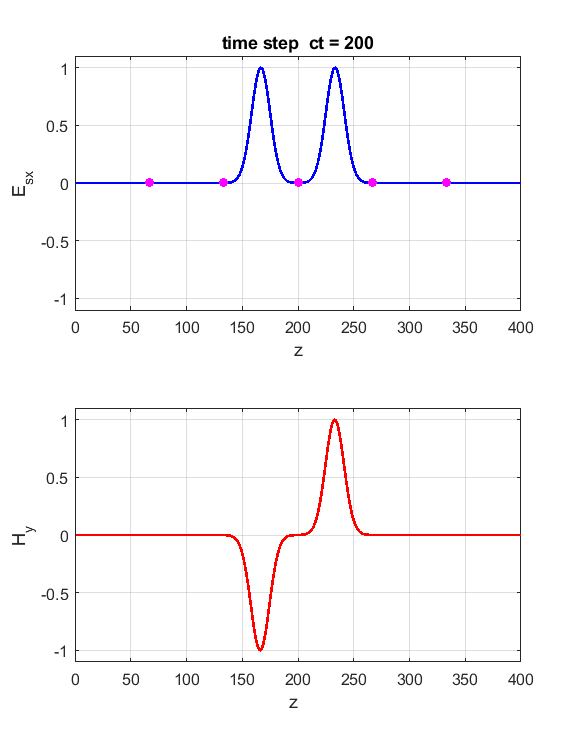
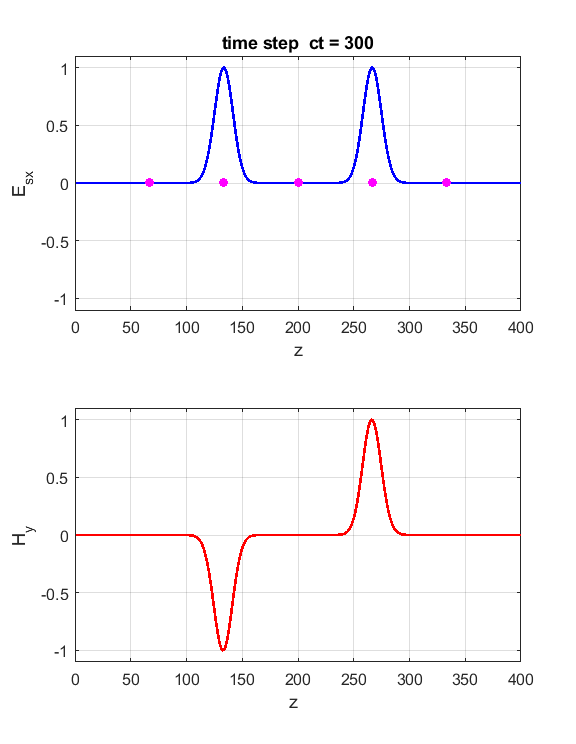
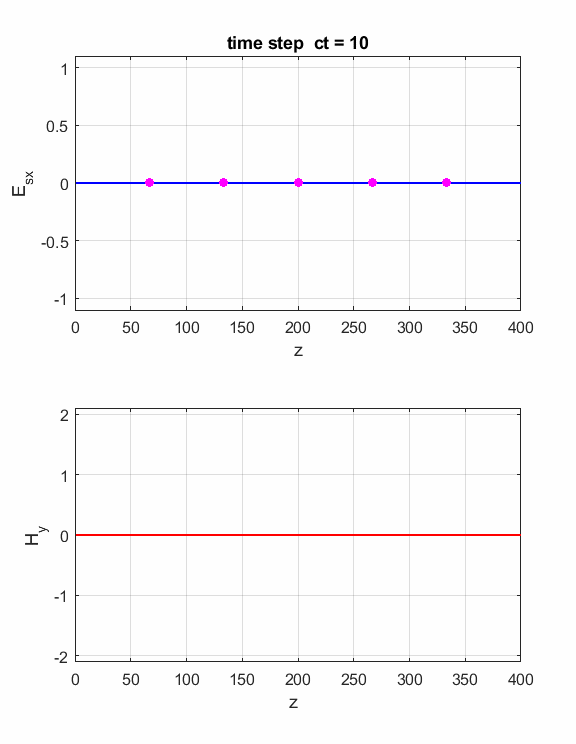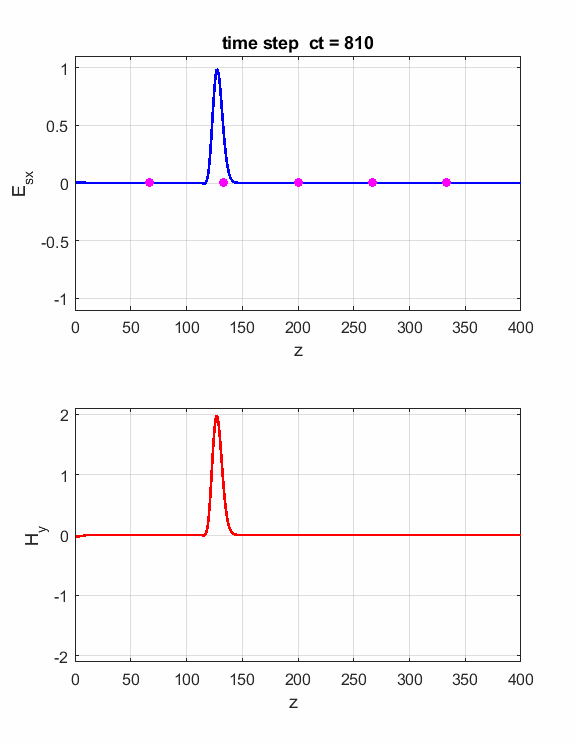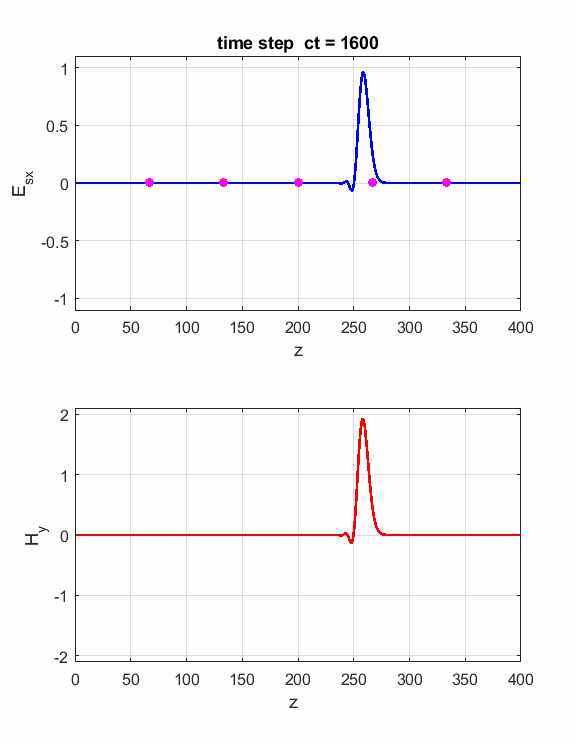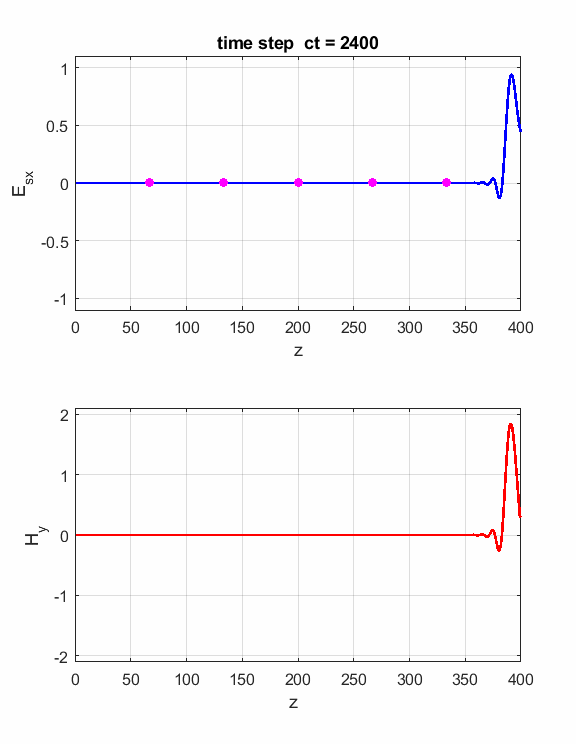
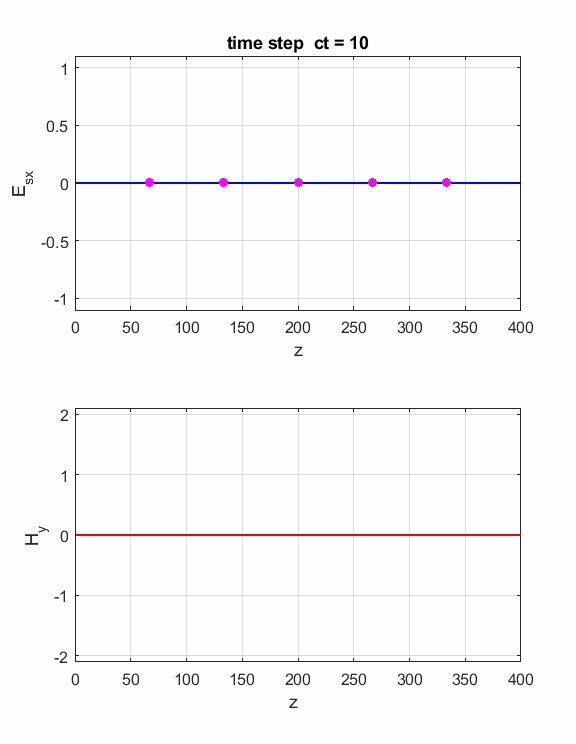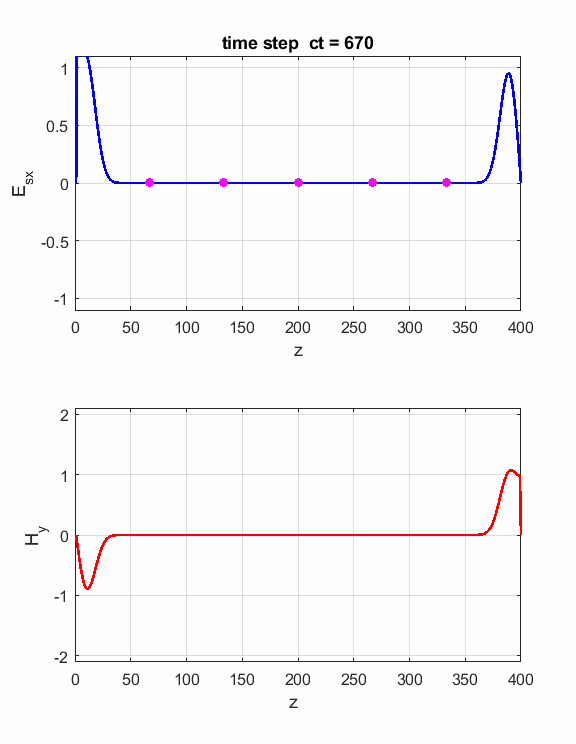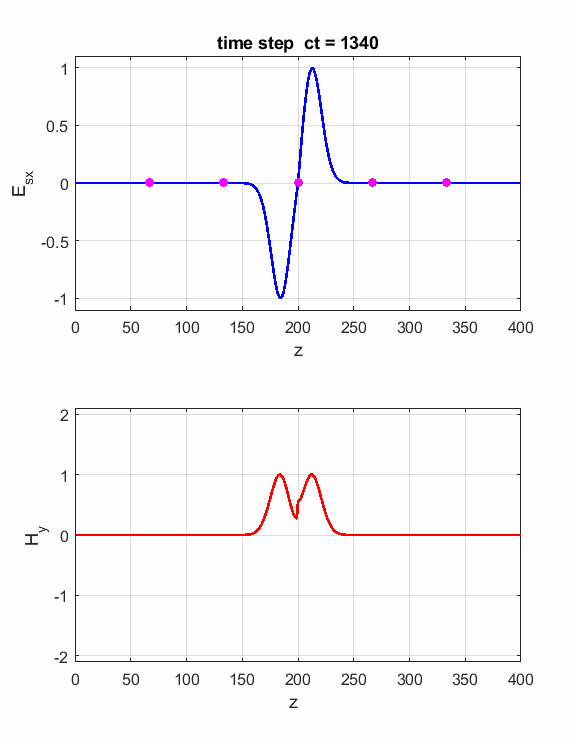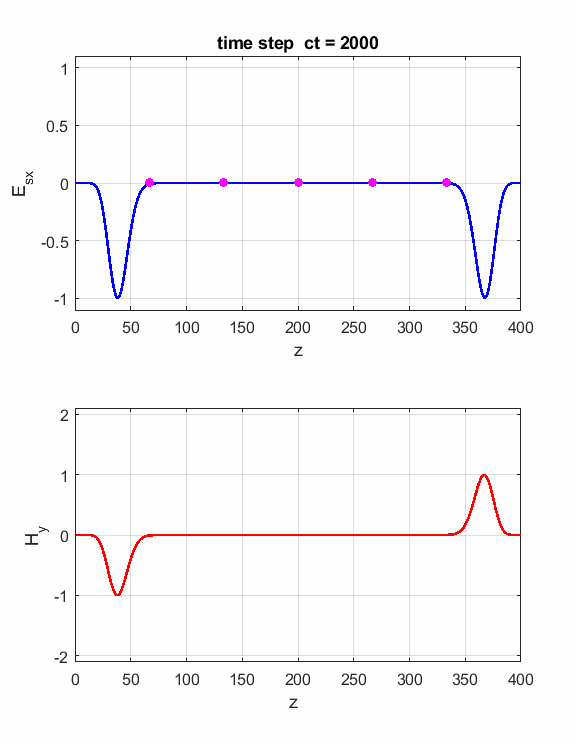
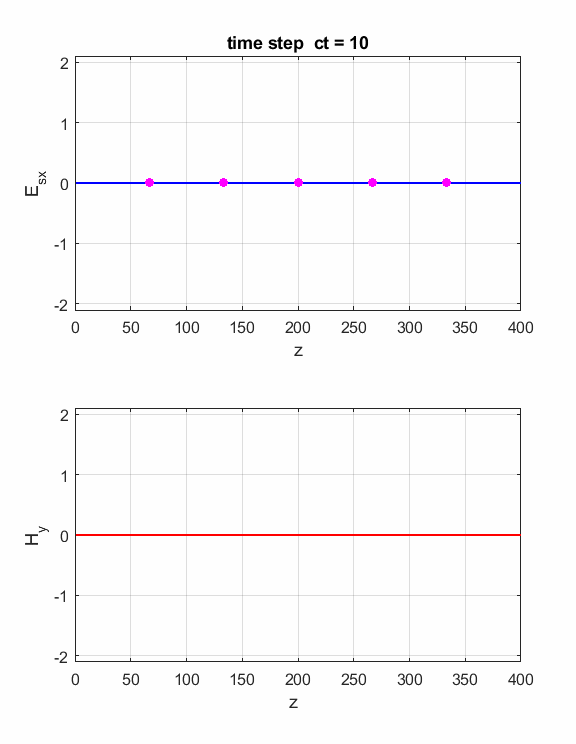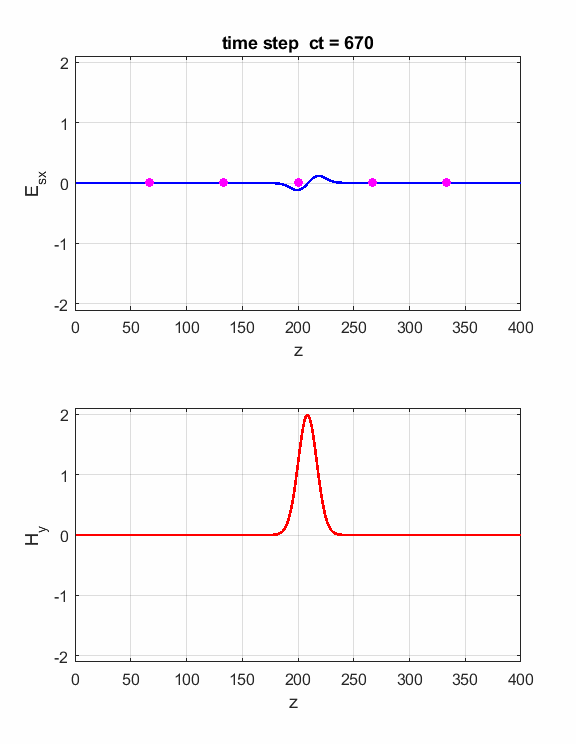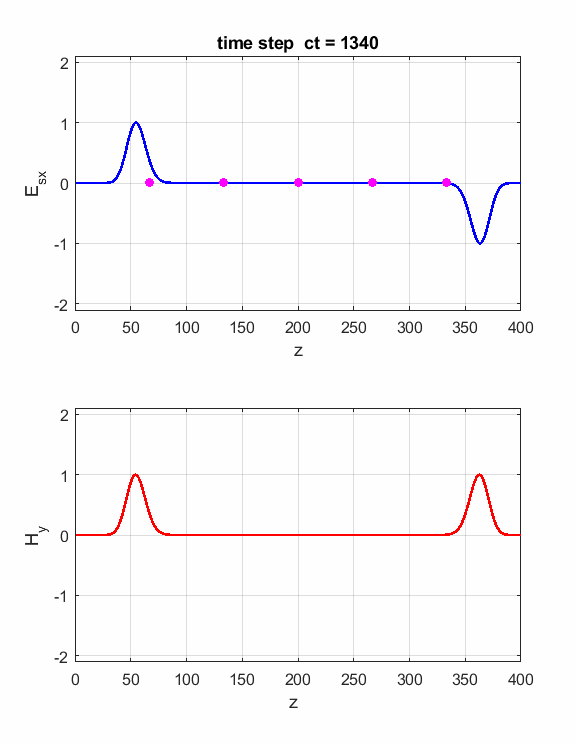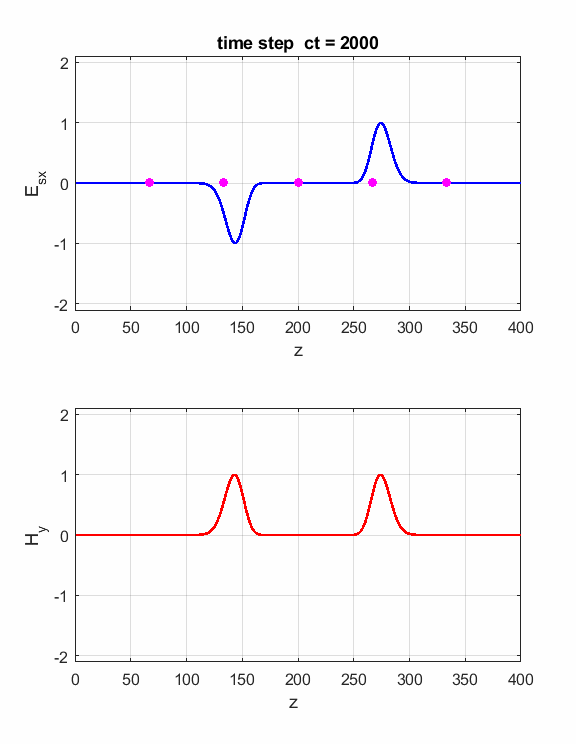
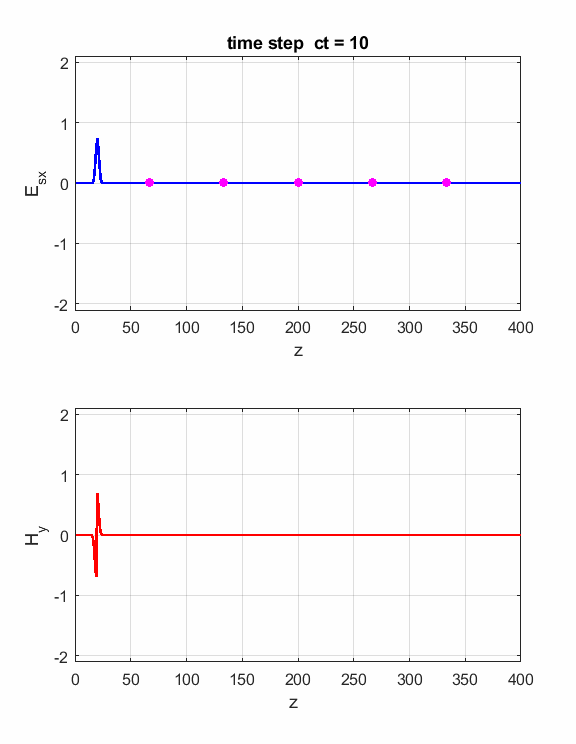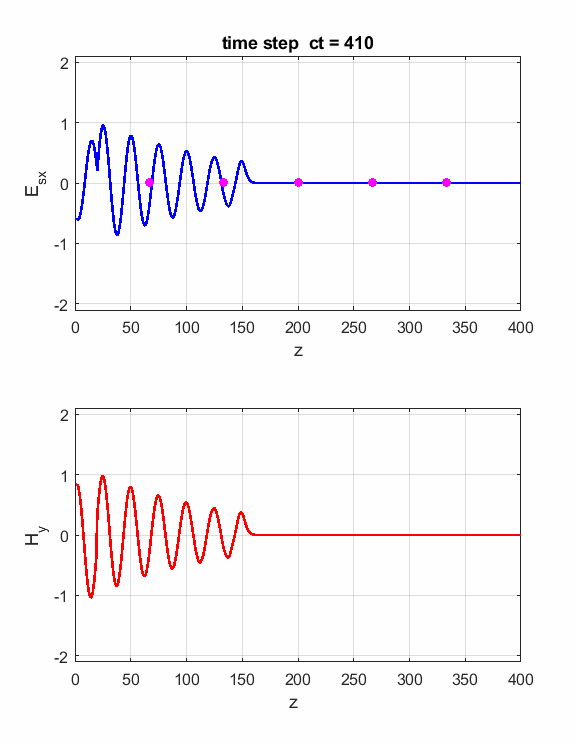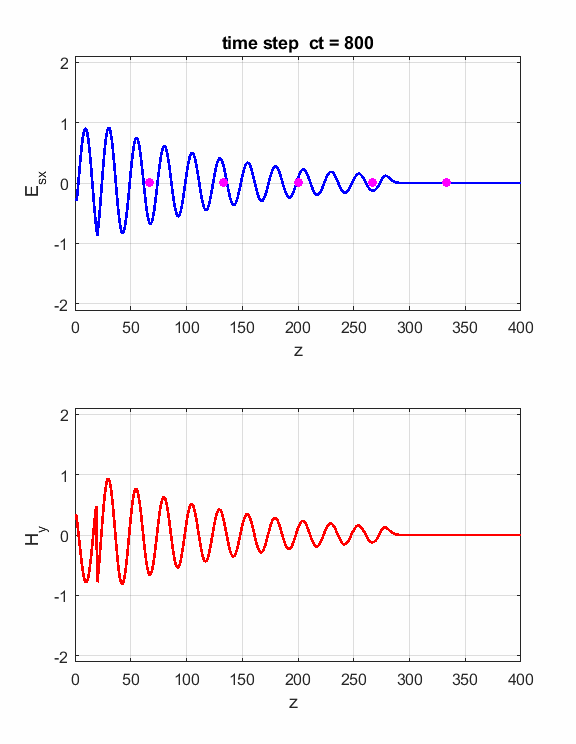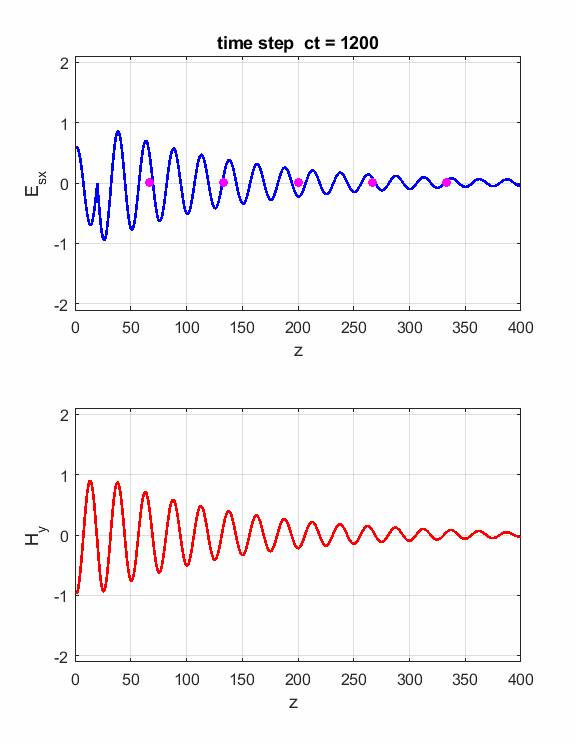
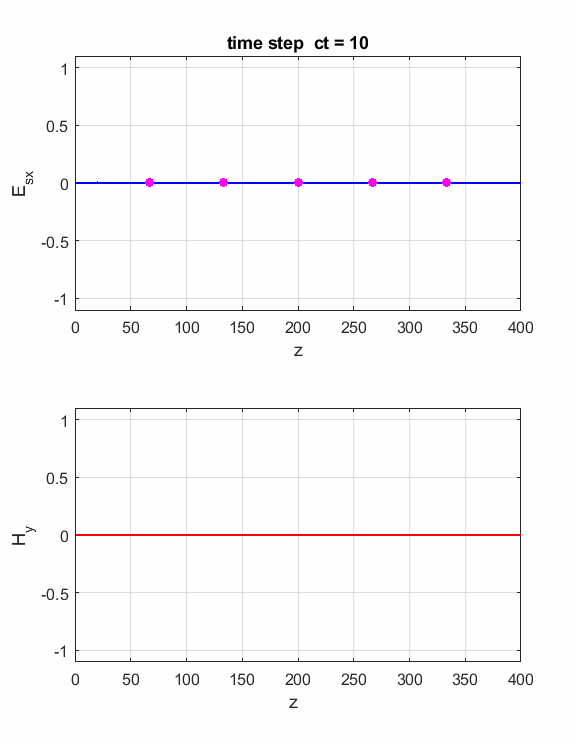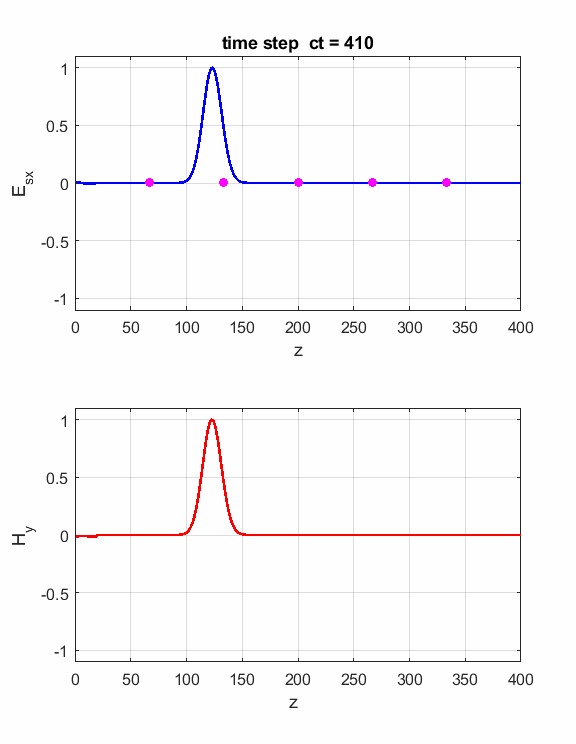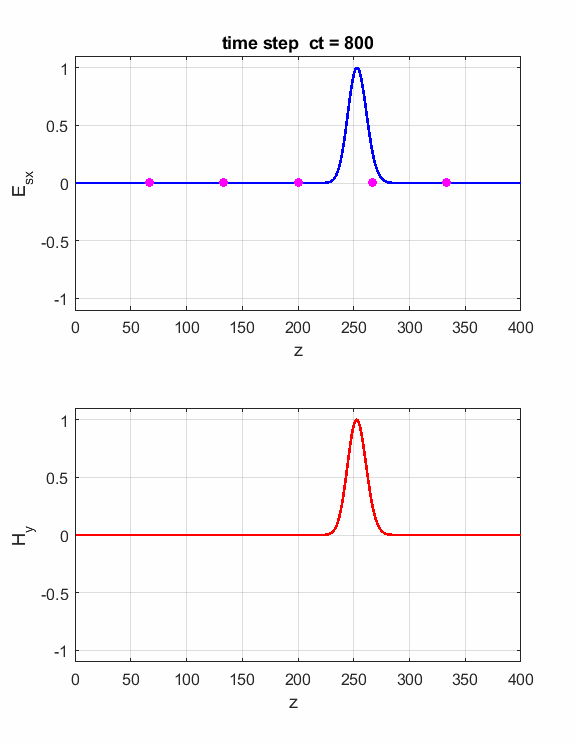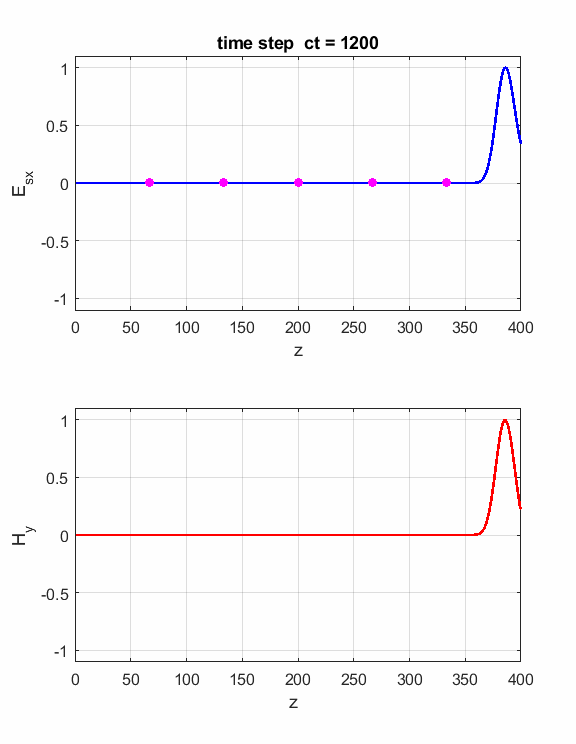
Fig. 2.   The electric field at five probe positions as functions of time. The time variation of the source electric field near z = 0 excites an electromagnetic wave that spreads from the source point. The wave propagates at the speed light in a vacuum c0. Time and position are not independent variables. The time step dt and the grid spacing dz are connected through the stability condition . This relationship implies that a wave travelling at the speed of light in a vacuum takes two time steps to travel one grid spacing.

 

Fig. 3. Animation of the propagation of the electromagnetic wave. The right-hand screw rule gives the direction of propagation. The fingers of the right-hand curl from the direction of Ex to the direction of Hy and then the thumb gives the direction of propagation. The energy in an electromagnetic wave resides in the medium through which it propagates, even in free space. The flow of energy is measured by the Poynting vector . Therefore, for a pulse propagating to the right (+Z direction) both Ex and Hy are positive. For the pulse propagating to the left (-Z direction) E­x and Hy must have opposite signs.

 

 

Fig. 4.   You can vary the number of time steps to view the position of the electromagnetic wave at different times.

 

 

Simulation 2     Propagation in non-magnetic and non-lossy uniform dielectric media

 

For a non-magnetic and non-lossy dielectric medium, the speed of propagation c of an electromagnetic wave depends on the refraction index n of the medium. The refractive index n is a function of the relative permittivity , hence

               

 

Fig. 5. Propagation of a Gaussian pulse in a medium with relative permittivity of 4. . The speed of propagation c is half the vacuum speed of light c0 and the magnitude of the Hy field is twice the value of the vacuum magnitude. For an electromagnetic wave the impedance Z is defined as the ratio between the magnitudes of the E and H fields. For a medium with dielectric constant  the impedance Z varies as  

           

   

      

       

 

The impedance of free space is .

 

Numerical results are displayed in Figure Window. For example, a pulse originating from the centre of Z space when eR1= 1 and eR2 = 4.

 

We can change the boundary conditions to set the electric field (PEC  flagBC = 2) or the magnetic field (PMC flagBC = 3) to be zero at the ends of the Z space.

Fig. 6.   Perfect Electric (PEC) boundary conditions. The Ex field and Hy field pulses are reflected at the ends of the Z space. The orientation of the fields is such that the direction of propagation of a pulse is given by the right-hand screw rule. As the pulses pass through each other they either interfere constructively or destructively.

 

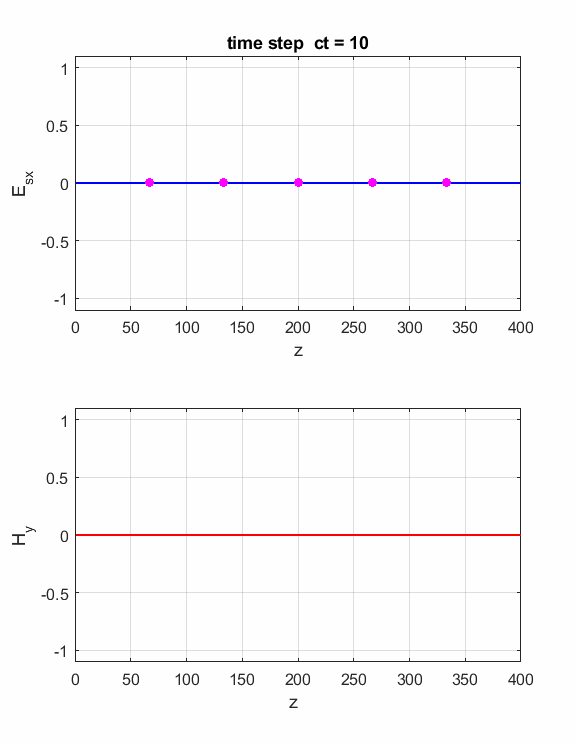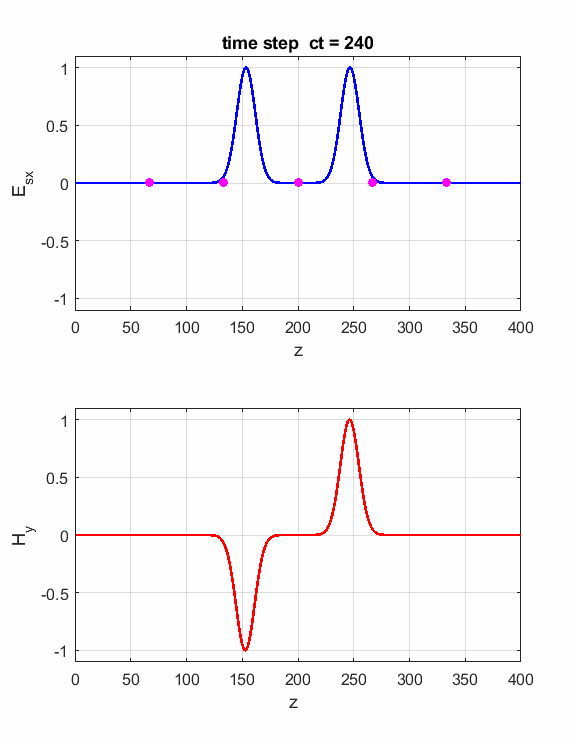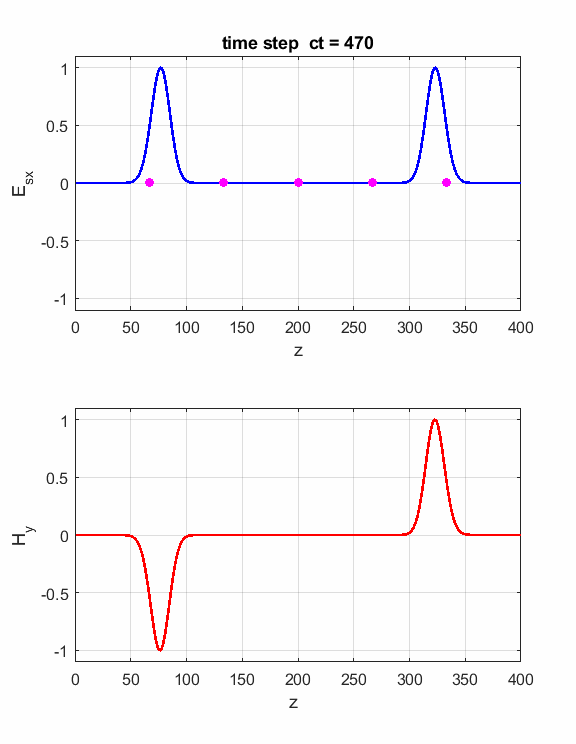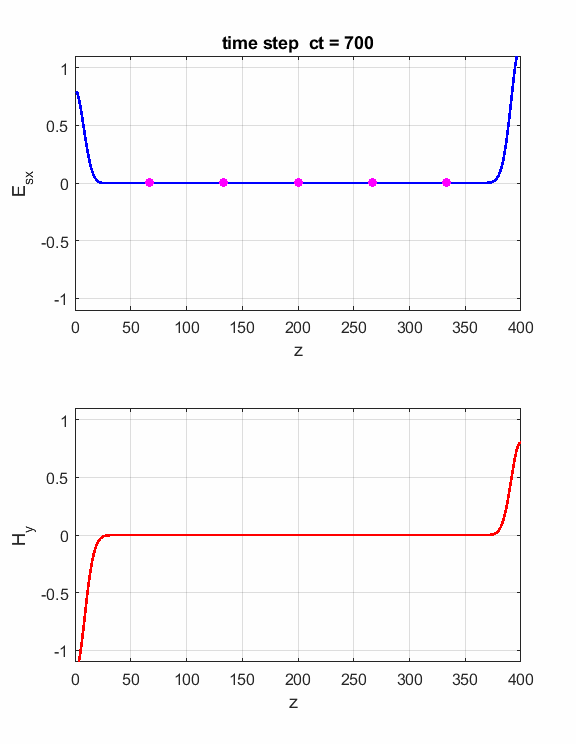
Fig. 7.   Perfect Magnetic (PMC) boundary conditions. The Ex field and Hy field pulses are reflected at the ends of the Z space. The orientation of the fields is such that the direction of propagation of a pulse is given by the right-hand screw rule.

 

 

We can introduce two pulse sources and study the interference effects as the two pulses pass through each other. Just add the code for the second source

            E(ct,zS) = source(ct);

            E(ct,Nz-2) = source(ct);

 

Fig. 8. Interference effects of two pulses. Depending on the phase of the two pulses, the pulses either interfere constructively or destructively as they pass through each other. The EM wave is reflected from the hard source.

 

 

 

Simulation 3     Propagation in non-magnetic and lossy uniform dielectric media

 

Fig. 9.   Propagation of sinusoidal EM wave in a lossy dielectric (eR = 0.025).