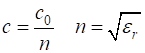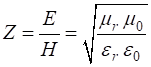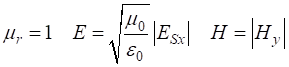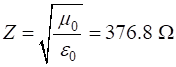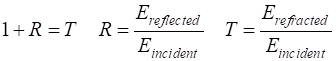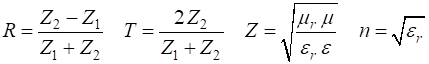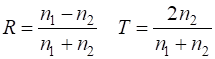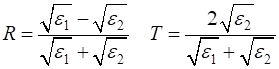[1D] FDTD electromagnetic wave simulations of propagating waves incident upon a boundary between two non-magnetic and non-lossy uniform dielectric media

Ian Cooper

Please email any corrections, comments, suggestions or additions

matlabvisualphysics@gmail.com

View ELECTROMAGNETISM USING THE FDTD METHOD

Matlab Download Directory

ft_03.m

Download and run the script ft_03.m. Carefully inspect the script to see how the FDTD method is implemented. Many variables can be changed throughout the script, for example, type of excitation signal, boundary conditions, time scales, properties of the medium.

A wave encountering a boundary between media with different refractive indices (relative permittivities) will in general be partially refracted (transmitted) and partially reflected at the boundary. The relationship between the incident wave and the refracted and reflected waves can be expressed in terms of the transmission T and reflection R coefficients. This relationship can be expressed in terms of impedances Z or refractive indices n.

For a non-magnetic and non-lossy dielectric medium, the speed of propagation c of an electromagnetic wave depends on the refraction index n of the medium. The refractive index n is a function of the relative permittivity , hence

For an electromagnetic wave the impedance Z is defined as the ratio between the magnitudes of the E and H fields. For a medium with dielectric constant the impedance Z varies as

The impedance of free space is .

For our [1D] model of the incident wave reaching the boundary, we must have

and

In the case of non-magnetic material , so

For example:

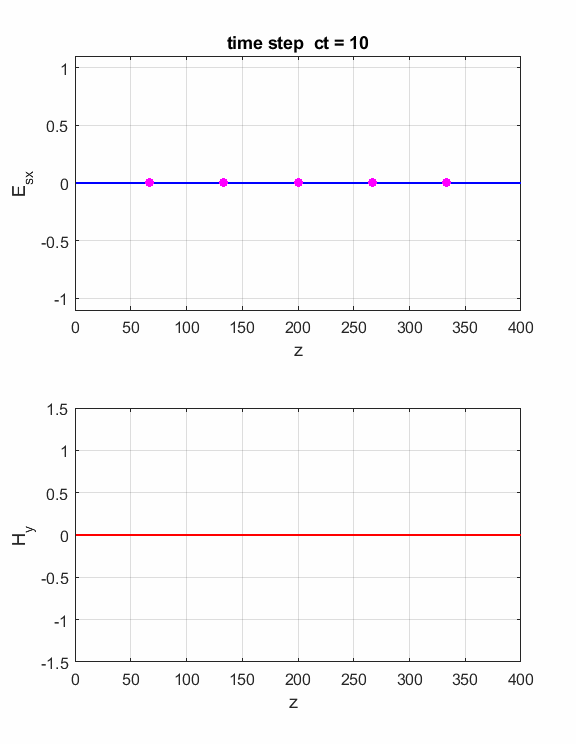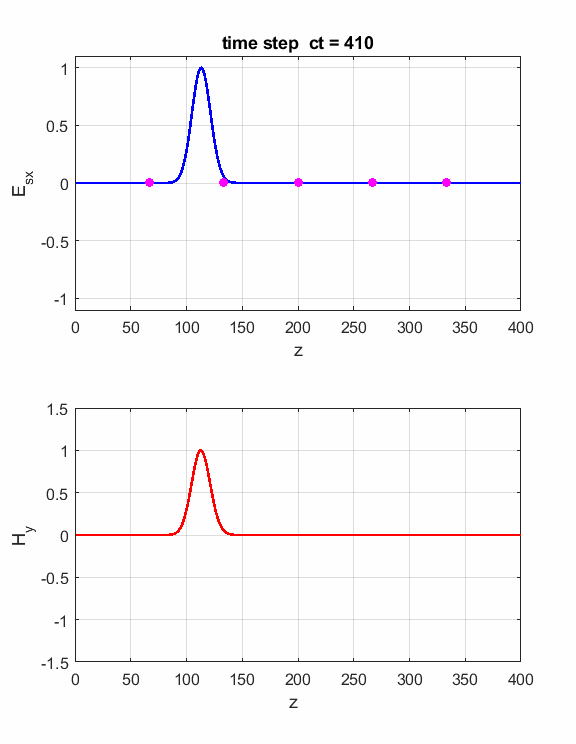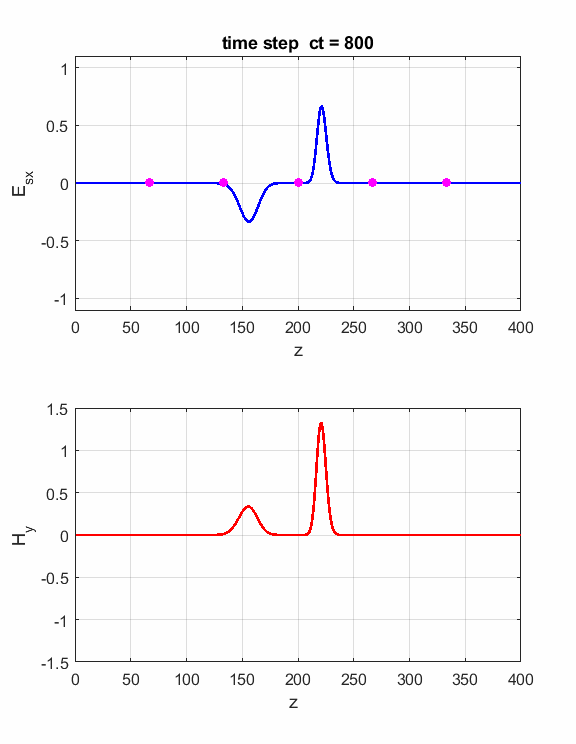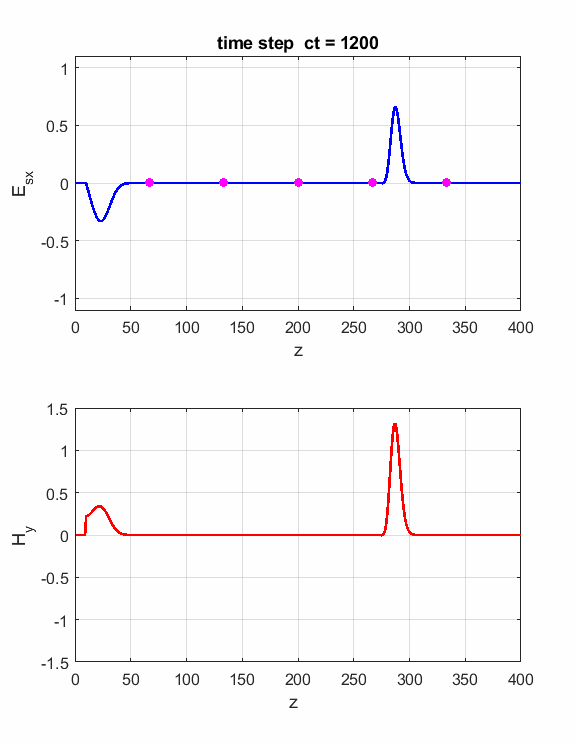
Simulation 1 EM wave incident upon a boundary between two media

Nz = 400 Number of grid points for Z space

flagS = 1 Pulse

zS = 10 Source: Z location

A = 1 Amplitude

width = 25 Width of pulse

centre = 100 Time step for centre of pulse

flagBC = 1 Absorbing boundary conditions

M2 = 200 Index for start of Medium 2

eR1 =1 S1 = 0 Relative permittivity & conductivity Medium 1

eR2 = 4 S2 = 0 Relative permittivity & conductivity Medium 2

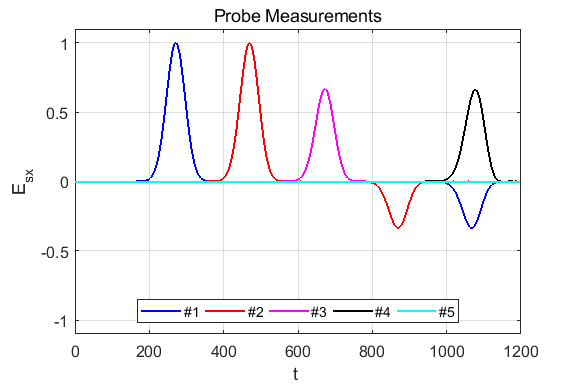
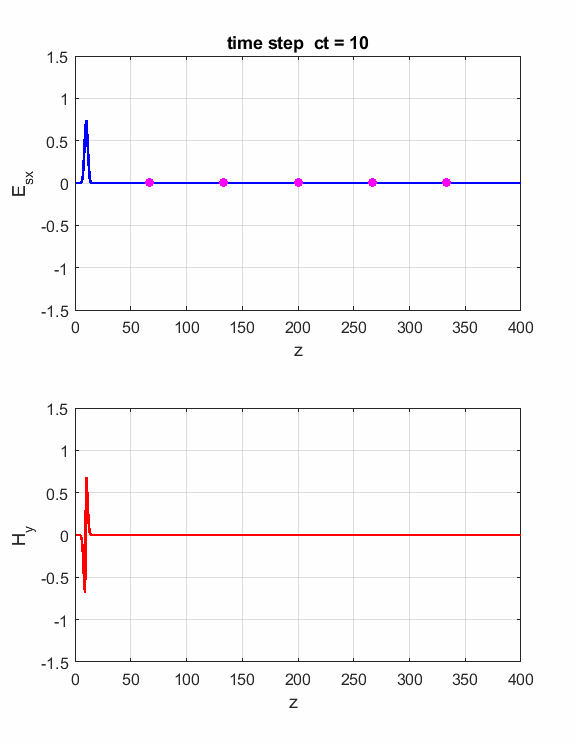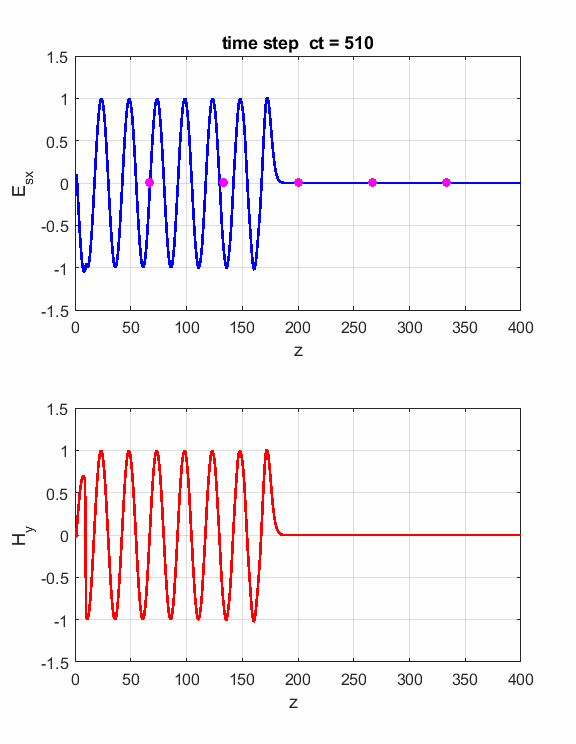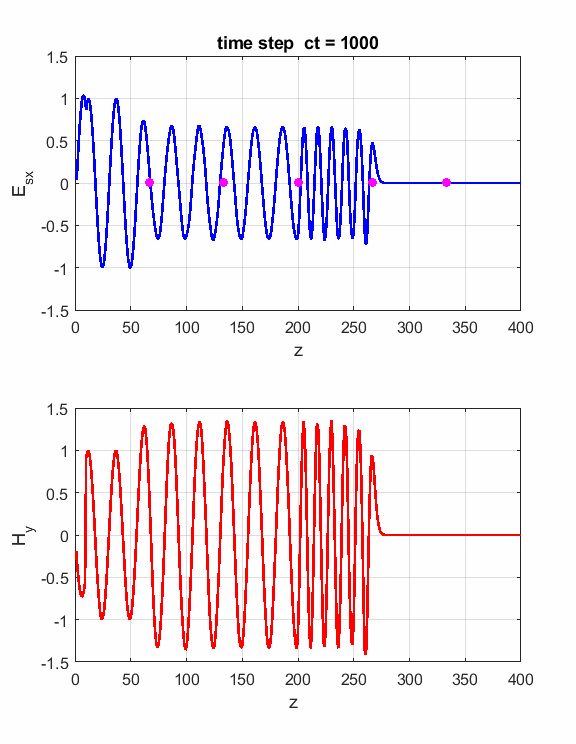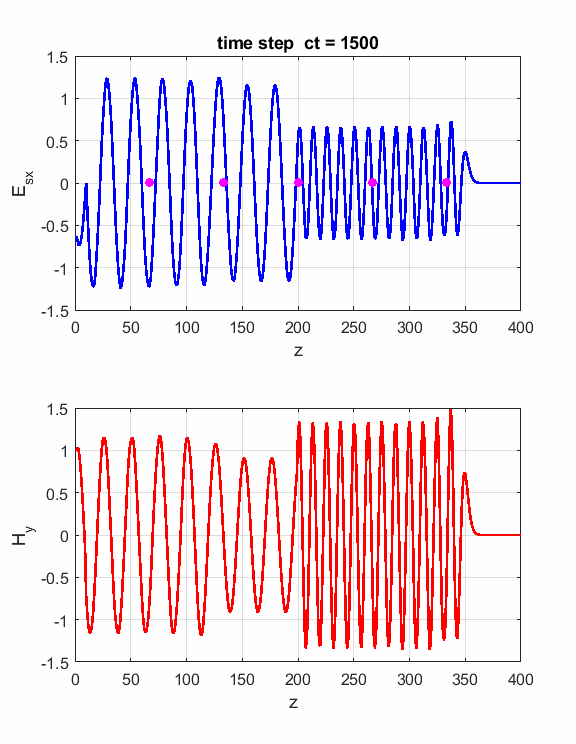
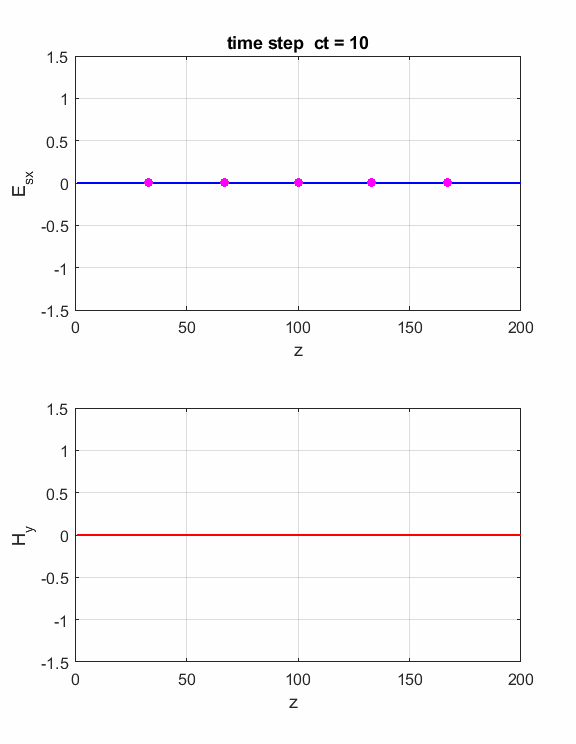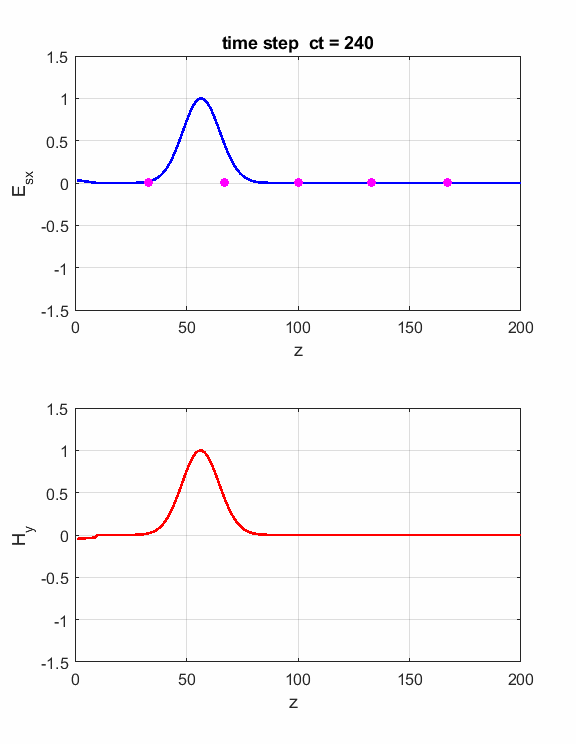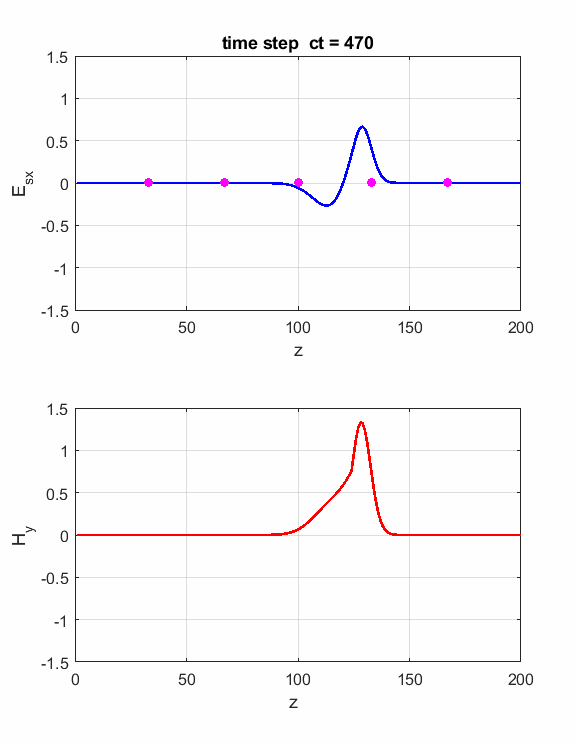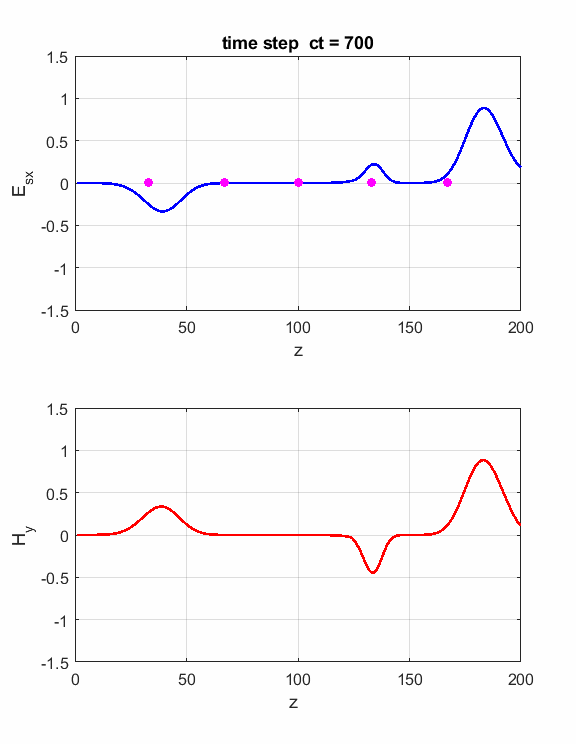
Fig.1. Animation of the electromagnetic pulse incident upon a boundary and probe measurements. The boundary is located at z = 200 . The incident electric field has an amplitude of 1. The magnitude of the reflected pulse is -0.33 and the magnitude of the transmitted pulse is 0.67. The speed of the transmitted pulse in medium 2 is c₀/ 2. The results of the simulation agree with the theoretical predictions.

We can also simulate the incident wave as a sinusoidal wave with frequency f = 400 MHz.

Fig.2. Animation of an electromagnetic sinusoidal wave (f = 400 MHz) incident upon a boundary and probe measurements. The boundary is located at z = 200 . The frequency of the transmitted wave is equal to the frequency of the incident wave. However, the wavelength of the transmitted wave decreases because the speed of the wave is lower in medium 2. The incident wave and reflected wave interfere with each other creating the pulsating effect as the waves reinforce each other (constructive interference) or partially cancel each other (destructive interference).

We can also study the changes of phases of an EM wave striking a barrier with a different refractive index. A dielectric slab with refractive index n = 2 (ER2 = 4) is located at between Z grid positions 125 and 150 as shown in figure 3.

An EM wave travelling in free space striking a dielectric slab. At the junction z = 125, the refractive index change from 1 to 2. The reflected pulse is inverted (phase change rad). At the end of the slab at z = 150, the refractive index changes from 2 to 1 and the reflected pulse is not-inverted (no change in phase).