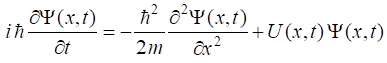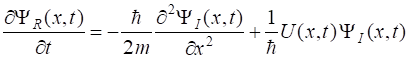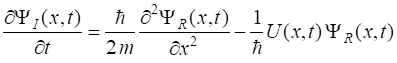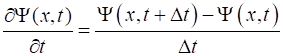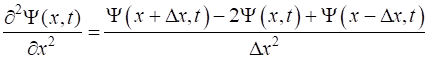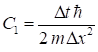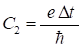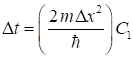DOING PHYSICS WITH MATLAB

MATLAB RESOURCES

QUANTUM MECHANICS

                  

Ian Cooper

 

matlabvisualphysics@gmail.com

 

 

TIME DEPENDENT SCHRODINGER EQUATION

FINITE DIFFERENCE TIME DEVELOPMENT METHOD

 

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

 

   GitHub

 

   Google Drive

 

 

The Schrodinger Equation is the basis of quantum mechanics. The state of a particle is described by its wavefunction  which is a function of position and time t. The wavefunction is a complex variable and one cannot attribute any distinct physical meaning to it.

 

We will consider solving the [1D] time dependent Schrodinger Equation using the Finite Difference Time Development Method (FDTD).

 

The one-dimensional time dependent Schrodinger equation for a particle of mass m is given by

        (1)      

 

where  is the potential energy function for the system.

 

The wavefunction is best expressed in terms of its real and imaginary parts

        (2)      

 

 

Inserting equation 2 into equation 1 and separating real and imaginary parts results in the following pair of coupled equations

 

        (3a)    

 

        (3b)    

 

 

We can now apply the finite difference approximations for the first derivative in time and the second derivative in space. The time step is  and the spatial grid spacing is . Time, position and the wavefunction are expressed in terms of the time index  and the spatial index

 

        Time                    

        

        Grid positions   

       

        Wavefunction is calculated at each time step nt

                               

 

where the symbol y is used for the wavefunction in the coding of the Script.

 

        (4)      

 

        (5)      

 

 

The second derivative of the wavefunction given by equation 5 is not defined at the boundaries. The simplest approach to solve this problem is to set the wavefunction at the boundaries to be zero. This can cause problems because of reflections at both boundaries. Usually, a simulation is terminated before the reflections dominate.

 

Substituting equations 4 and 5 into equations 3a and 3b and applying the discrete times and spatial grid gives the latest value of the wavefunction expressed in terms of earlier values of the wavefunction at each time step are calculated from equations 6a and 6b

 

        (6a)

              

 

          (6b)     

               

 

 

where the constants C1 and C2 are

 

          (7)             and    

 

 

 

for nt = 1 : Nt-1

   for nx = 2 : Nx - 1

      yR(nx) = yR(nx) - C1*(yI(nx+1)-2*yI(nx)+yI(nx-1)) + C2*U(nx)*yI(nx);

    end

   psiR(nt+1,:) = yR;

  

   for nx = 2 : Nx-1

      yI(nx) = yI(nx) + C1*(yR(nx+1)-2*yR(nx)+yR(nx-1)) - C2*U(nx)*yR(nx);

   end

    psiI(nt+1,:) = yI;

end

for nt = 2:Nt

  psiI(nt,:) = 0.5*(psiI(nt,:) + psiI(nt-1,:));

end

 

 

The potential U is given in electron-volts (eV) and to convert to joules, the charge of the electron e is included in the equation for the constant C2.

 

In equations 6a and 6b, the y variables on the RHS gives the values of the wavefunction at time  and the y variables on the LHS are the values of the wavefunction at time t. Hence, given the initial values of the wavefunction, equations 6a and 6b explicitly determine the evolution of the system. The FDTD method can “blow-up” if appropriate time increments or grid spacings are not used. For a given grid spacing  we will set  which means the time increment  is determined by    

          (8)    

 

 

It is a relatively easy task to model an electron in a system with a potential energy function  in the region  to. The potential energy function will be considered to be time independent. However, you can easily input a potential energy function that does depend upon time.