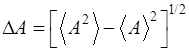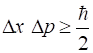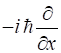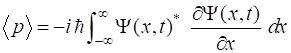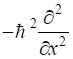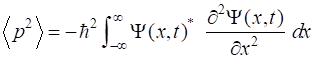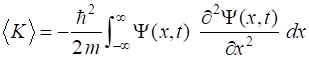DOING PHYSICS WITH MATLAB

MATLAB RESOURCES

QUANTUM MECHANICS

                  

Ian Cooper

 

matlabvisualphysics@gmail.com

 

 

WAVEFUNCTION: OBSERVABLES, EXPECTATION VALUES,

UNCERTAINTIES, HEISENBERG UNCERTAINTY PRINCIPLE

 

 

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

 

   GitHub

 

   Google Drive

 

simpson1d.m      used to evaluate all [1D] integrals

 

QMG24D.m        Propagation of a quantum-mechanical Gaussian pulse (example

                             of calculating expectation values)

 

 

EXPECTATION VALUES OF OBSERVABLES

 

The wavefunction  itself has no definite physical meaning, however, by performing mathematical operations on the wavefunction we can predict the mean values (expectation values) and their uncertainties of physical quantities such as position, momentum and energy.

 

The expectation value of an observable quantity A is the quantum-mechanical prediction for the mean value of A.

 

We will consider a particle to be an electron and that we know the wavefunction  for the system of the single electron. Since an electron does exist within the system, the probability of finding the electron is 1.

        (1)                   

 

The quantity  is called the probability density function.

 

The probability of finding the electron in the region from  to  is

        (2)      

 

 

Consider N identical systems, each containing an electron. We make N identical measurements on each system of the physical parameter A. In a quantum system, each measurement is different. From our N measurements, we can calculate the mean value  and the standard deviation  of the parameter A.  Since we do not have a complete knowledge of the system, we only can estimate probabilities.

       

The mean value of an observable quantity A is found by calculating its expectation value  by evaluating the integral

        (3)      

 

where  is the quantum-mechanical operator corresponding to the observable quantity A,

and its uncertainty is the standard deviation of A. The uncertainty  is given by

        (4)                       

 

        (5)      

 

The quantity represents the probability distribution for the observable A and is often shown as a probability density vs position graph.  Probability distributions summarize the extent to which quantum mechanics can predict the likely results of measurements. The probability distribution is characterized by two measures – its expectation value which is the mean value of the distribution and its uncertainty which is the represents the spread in values about the mean and is given by the standard deviation. The R.H.S. of the integrals (3) and (5) are known as sandwich integrals.

 

 

For our [1D] system, a particle in any state must have an uncertainty in position  and uncertainty in momentum  that obeys the inequality called the Heisenberg Uncertainty Principle

        (6)      

 

The Heisenberg Uncertainty Principle tells us that it is impossible to find a state in which a particle can has definite values in both position and momentum. Hence, the classical view of a particle following a well-defined trajectory is demolished by the ideas of quantum mechanics.

 

Table 1 gives a summary of the most important operators for [1D] quantum systems. Expectation values maybe time dependent.

 

   Table 1.  Observables, Operators and Expectation values

Observable

Operator

Expectation Value

probability

1

 

position

x

 

x2

x2

 

momentum

 

 

 

p2

 

 

 

Potential energy

U

 

Kinetic energy

K