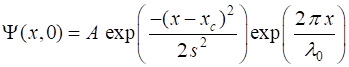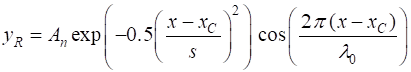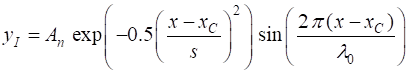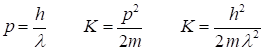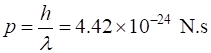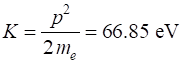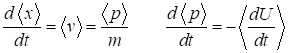MATLAB RESOURCES

QUANTUM MECHANICS

Ian Cooper

matlabvisualphysics@gmail.com

TIME DEPENDENT SCHRODINGER EQUATION

FINITE DIFFERENCE TIME DEVELOPMENT METHOD

FREE PARTICLE: GAUSSIAN WAVEPACKET PROPAGATION

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

GitHub

Google Drive

simpson1d.m Function for [1D] integration

QMG24D.m Propagation of Gaussian wavepacket

ColorColde.m A function used to represent the complex phase of the Gaussian wavepacket as a coloured sequence.

LINKS

[1D] time dependent Schrodinger Equation using the Finite Difference Time Development Method (FDTD). link

Expectation values link

GAUSSIAN PULSE PROPAGATION

As an example of solving the[1D] time dependent Schrodinger equation for a free particle (unbound particle), let’s consider an electron confined to the X axis in the region from to . The electron is represented by a wavepacket to localize it. An initial state described by the Gaussian function is

where A is a normalized constant and is calculated so that , x_c is the centre of the Gaussian wavepacket, s determines its width and is the wavelength. The time evolution of the wavepacket is found from its initial state by solving the [1D] time dependent Schrodinger Equation using the Finite Difference Time Development Method (Script QMC24D.m).

This unbound state is in a classically allowed region and so the energies of the system are not quantized and the total energy E can vary continuously.

In the Script QMC24C.m, the initial state (t = 0) of the wavepacket is expressed in terms of its real (yR) and imaginary (yI) parts:

yR = exp(-0.5.*((x-x(nx1))./s).^2).*cos((2*pi).*(x-x(nx1))./wL);

yI = exp(-0.5.*((x-x(nx1))./s).^2).*sin((2*pi).*(x-x(nx1))./wL);

The particle represented by a wavepacket is localized in space with an approximately well-defined momentum or wavelength . However, the momentum or wavelength are not precisely defined for a wavepacket as momentum is not an eigenfunction but a mixture of momentum of eigenfunctions with a whole range of momentum values centre around .

nominal or peak or centre momentum of wavepacket

nominal or peak or centre wavelength of wavepacket

When the wave packet strikes a boundary at x = 0 or x = L, reflections occur. This may cause problems, so it may be necessary to terminate a simulation before any reflections occur.

The accuracy of the FDTD method is improved as and are made smaller. The numerical predictions are more accurate and consistent with a large value of . should always be an odd number, otherwise the integrations by Simpson’s rule will give wrong results.

Simulation parameters for Script QMC24D.m

Nx = 701 number of grid points for x-axis

Nt = 7000 number of time steps

L = 5x10^-9 m simulation region

xC = 1x10^-10 m centre of pulse

S = L/25 width of pulse

= 1.5x10^-10 m wavelength

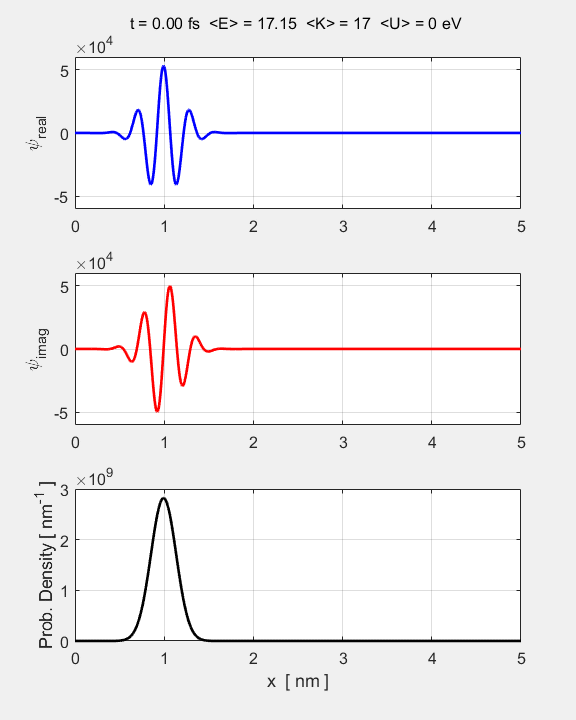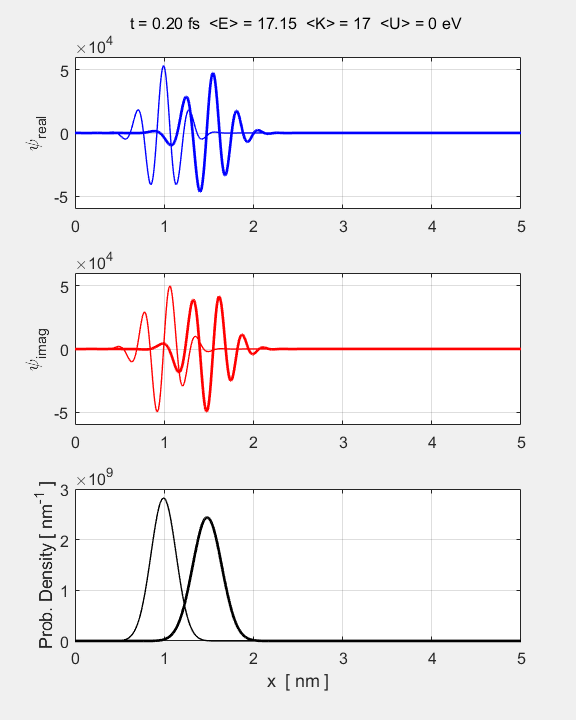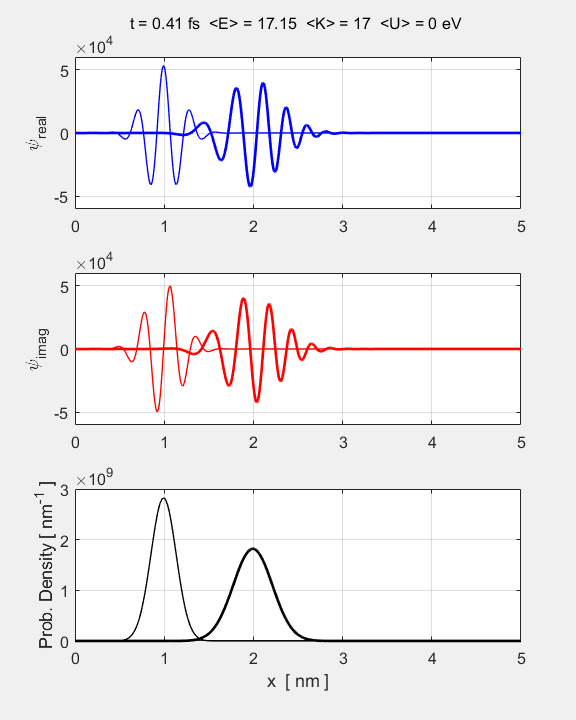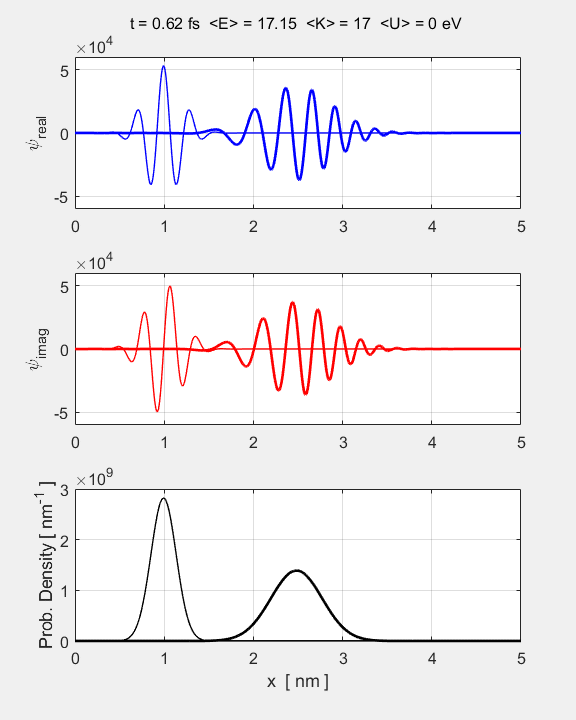
An animation of the time evolution of the Gaussian wavepacket is shown in figure 1.

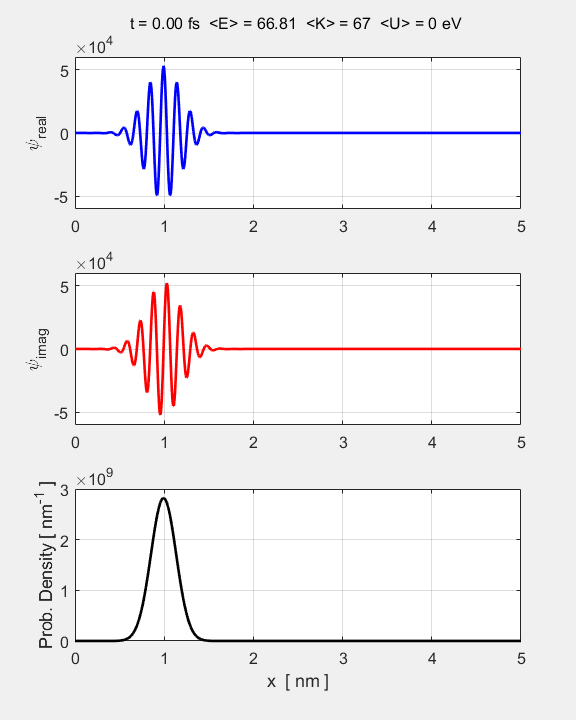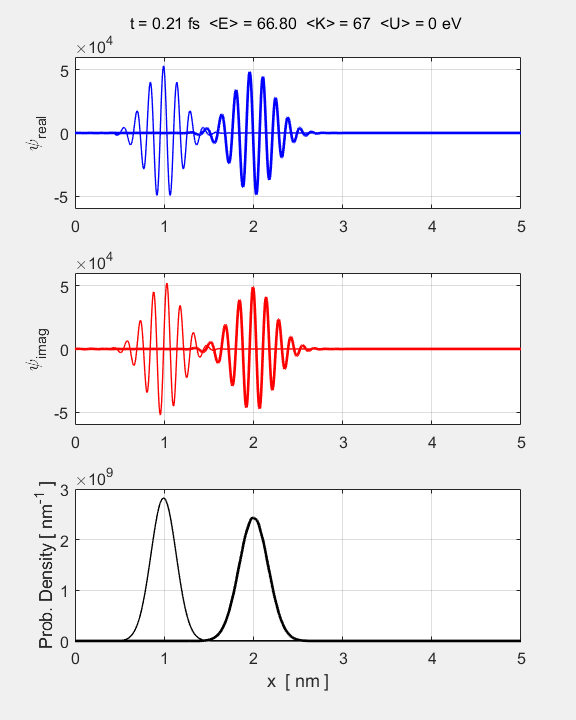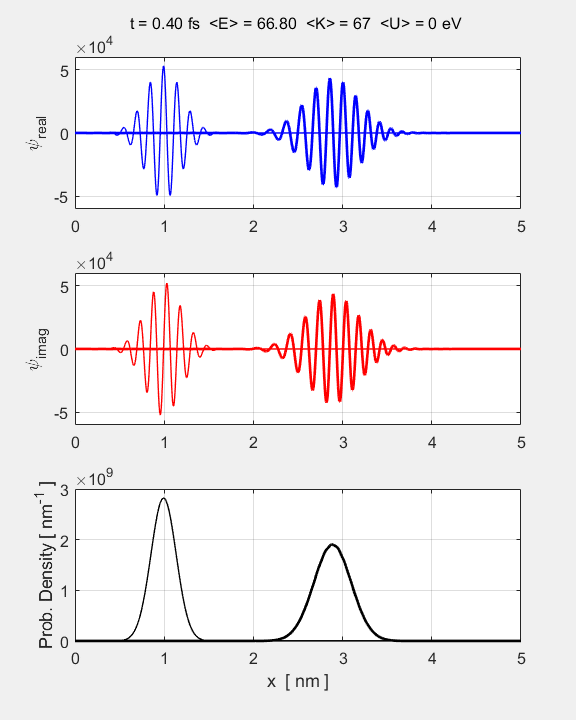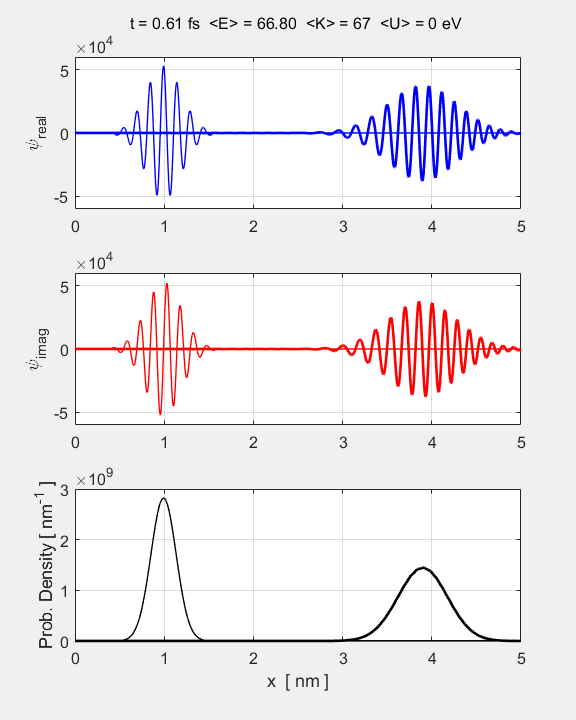
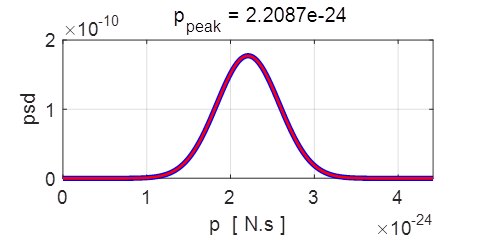
Fig. 1. Animation of the Gaussian wavepacket from its initial state. The top graph shows the real part of the wavefunction, the middle graph the imaginary part, and the bottom graph, the probability density.

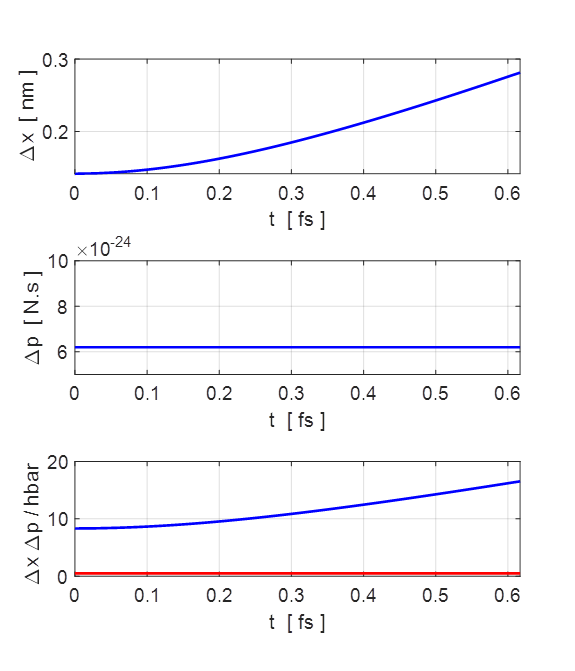
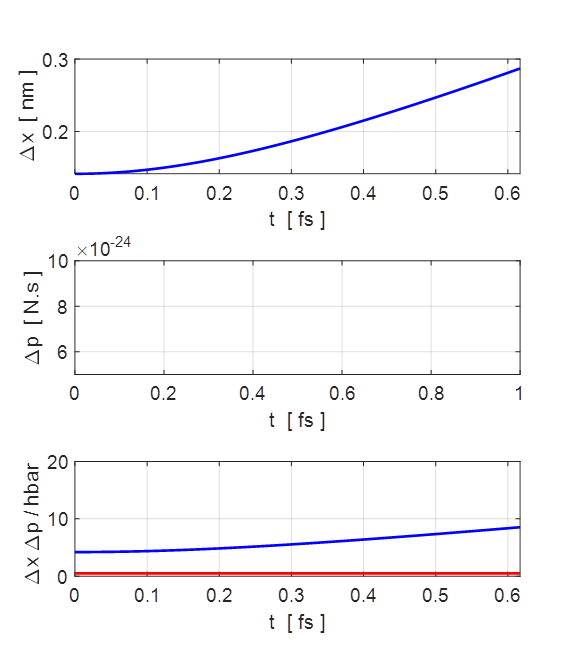
Fig. 2. The uncertainties in the position and momentum , and the product of the uncertainties . The Heisenberg Uncertainty Principle is satisfied since .

You will notice that the width of the wavepacket grows with time, i.e., wavepacket spreading.

Although, the wavefunction develops real and imaginary parts, both of which have lots of wiggles, the probability density turns out to be another Gaussian function with a width that increases with time. Eventually, the width of the wavepacket is proportional to time (figure 2).

The initial wavefunction has a spread of momentum and this distribution of momentum remains constant for a free particle because there are zero forces to change it. Since there is a spread in possible momenta, there is also a spread in velocities . This spread in velocities gives rise to the uncertainty in position of the particle that increases with time.

The wavepacket as it spreads propagates in the +X direction. Since there are zero forces acting on the system, the momentum of the wavepacket is constant, as a result, the expectation values of momentum, total energy, kinetic energy and potential energy are constants, independent of time.

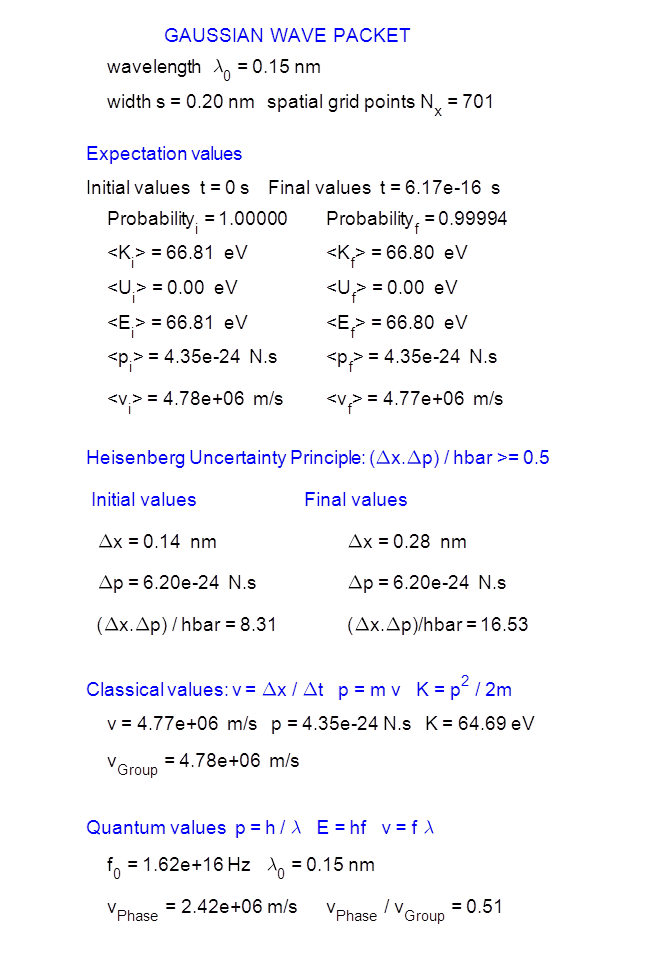
In the time evolution of the wave packet the Heisenberg Uncertainty Principle is satisfied. You can decrease the width of the wavepacket and run a simulation. You will notice that decreasing the spatial width of the initial wave packet increases the spread of momenta and therefore increases the rate at which the wavepacket spreads.

Table 1. Summary of the simulation parameters and computed results. The classical values are determined by the calculating the velocity from the distance travelled by the pulse in the time interval (). The classical velocity is the speed at which the centre of the wavepacket propagates and this speed is called the group velocity . For the wave nature of the wavepacket, the momentum and energy are given by the equations and where the subscript 0 indicates the nominal value. If you inspect the animation of the propagation of the wavepacket, you will observe “ripples” moving within the wavepacket and they propagate at the nominal phase velocity, . The wavepacket as a whole moves at the group velocity which is twice as fast as the ripples within it moving at the phase velocity, or

The wavepacket is a mixture of waves moving at a whole range of velocities, so as it moves along, some of these components move faster than others. Soon this dispersion causes the wavepacket to spread out (just as a large group of hikers naturally spreads out along the trail, with the faster

ones in the lead and the slower ones behind). Although the wavelength of the oscillations within the packet is initially uniform, it will not remain uniform. The wavepacket moves and spreads, its leading edge will contain shorter-wavelength (higher-velocity) oscillations, while its trailing edge will contain longer-wavelength (lower-velocity) oscillations. Meanwhile the peak amplitude of the wavepacket will decrease, to conserve probability as the width increases as illustrates in the animation of figure 1.

The initial kinetic energy K and its momentum p of our electron (mass m_e) can be estimated from its wavelength using the equations of classical physics and de Broglie’s equation

Using the default values for the simulations:

U = 0 eV

which are in agreement with the expectation values given in Table 1.

All that can happen to a classical particle is that it can move from one position to another. But, a quantum mechanical wavepacket undergoes a more complicated evolution with time in which the whole probability distribution shifts and spreads with time. The Ehrenfest’s theorem is a general statement about the rates of change of and in quantum-mechanical systems.

Ehrenfest’s theorm

If a particle of mass m is in a state described by a normalized wavefunction in a system with a potential energy function , the expectation values of position and momentum of the particle obey the equations

In this simulation, you can see that Ehrenfest’s theorem is satisfied. The momentum and its uncertainty remain constant. The distance d that the peak of the probability distribution moves in the time interval is

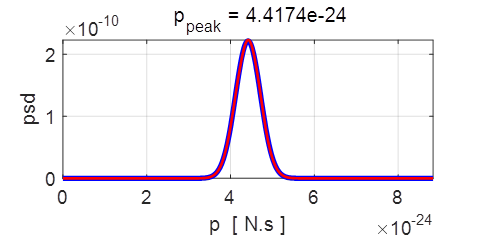
We can perform a Fourier transform on the wavepacket function to compute the power spectrum density (psd) in momentum space . Figure 3 shows the psd in momentum space for =0.15 nm and =0.30 nm

Fig. 3. Power spectral density functions in momentum space ( blue: t(0), red; t(end) ). The Fourier transform of a Gaussian function is a Gaussian function. Top graph (=0.15 nm) and bottom graph (=0.30 nm). Doubling the wavelength results in a halving of the nominal momentum and a wider spectral distribution in momenta. The width of the Gaussian psd function is independent of the width of the Gaussian function representing the wavepacket, and independent of time.

The Fourier transform is computed by integration of the Fourier integral and not by the FFT method

% Fourier transform PSI at t = 0 K = 1/wL

xMin = 0; xMax = L;

KMax = 2/wL0; KMin= -KMax; nK = 2001;

K = linspace(KMin,KMax,nK);

hP = psiR(1,:); HP = zeros(1,nK);

for c = 1:nK

g = hP.* exp(1i*2*pi*K(c)*x);

HP(c) = simpson1d(g,xMin,xMax);

end

% HP = HP./max(HP);

psd = conj(HP).*HP;

hP = psiR(Nt,:); HP = zeros(1,nK);

for c = 1:nK

g = hP.* exp(1i*2*pi*K(c)*x);

HP(c) = simpson1d(g,xMin,xMax);

end

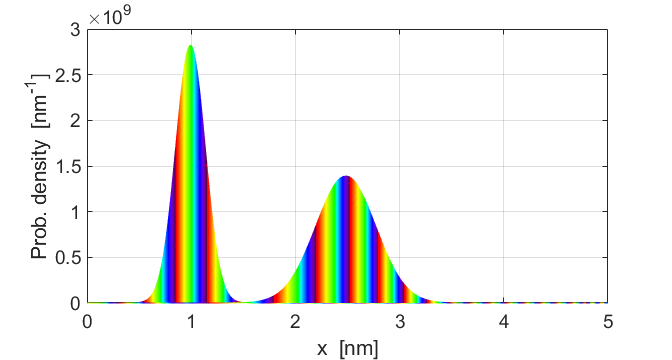
You can also visualize the complex phase of the wavepacket, where a colour is used to represent the phase between the real and imaginary components. Figure 4 shows the complex phase of the Gaussian wavepacket at the start and end of the simulation period. Figure 5 shows an animation of the changing complex phase changes as the wavepacket propagates. The Script runs very slowly when the animation shown in figure 5 is displayed in a Figure Window.

Fig. 4. The complex phase of the Gaussian wavepacket at the start and end of the simulation period.

Fig. 5. Animation of the complex phase as the Gaussian wavepacket propagates.

The following results are the outputs displayed by running the simulation with a doubling of the nominal wavelength. Since the nominal wavelength is doubled, then the nominal momentum and group velocity are halved. So, the wavepacket will only travel half the distance in the same time interval of 0.62 fs.