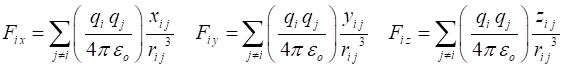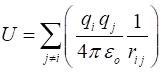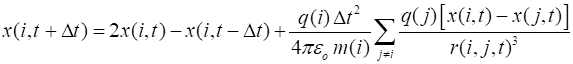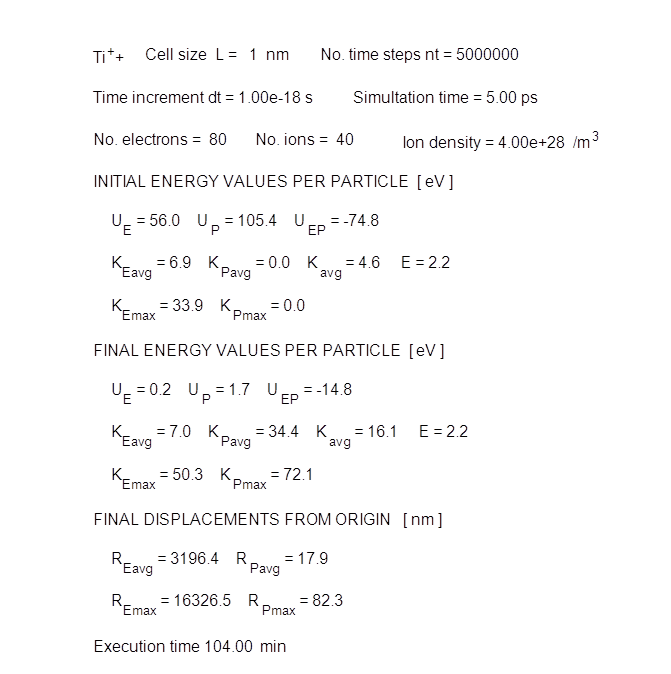DOING PHYSICS WITH MATLAB

MOLECULAR SIMULATIONS OF CATHODIC ARC PLASMAS

CATHODE SPOTS

Ian Cooper

matlabvisualphysics@gmail.com

I. J. Cooper and D. R. McKenzie, All particle simulations of cathodic arc plasmas, J. Applied Physics 99 093304, 2006

MATLAB SCRIPTS (download files)

emCathodeSpot.m

Script for the simulation of the early stages of the explosive expansion of a fully ionized cathode spot cathodic arc plasma from a localized initial volume. The equation of motion for the Coulomb interactions between all the electrons and positive ions is solved using a finite difference method.

For stability, a very small time step is used (dt = 1.00x10^-18 s) and the number of time steps can be high as several million. A simulation with 200 particles and 5x10⁶ time steps took about five hours on a fast desktop computer. The execution time is very dependent upon the number of particles. It took about 8 minutes for a 100 particle / 1x10⁶ time step simulation.

The plasma is assumed to be neutral. So, for a simulation with N particles, the number of electrons and positive ions are determined by the charge on the positive ions. For singularly charged ions, the number of electrons and positive ions are equal. The default ion used in the simulation is Ti⁺. The numbers 1 and 2 with a variable name are used to specify the variables for the electron and positive ions respectively.

The particles are initially located at random within a cube of side dimension L. Typical values of L are 1x10^-8 m and 1x10^-9 m. The side dimension L is a most critical factor, since it determines the initial density of the ions. The smaller the value of L, then the greater the explosive nature of the expansion of the plasma.

It is assumed that the positive ions are initially at rest while the electrons move in random directions with a Maxwellian velocity distribution. The default temperature of the hot electrons is TE = 3.0x10⁴ K.

You can apply a constant electric field Ex to give a constant force which act acts in the X direction on the charged particles.

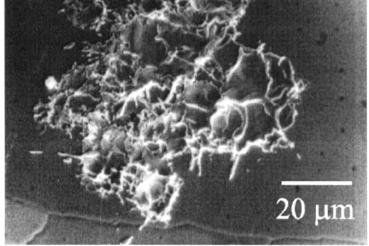
CATHODE SPOTS

Cathodic or vacuum arc plasma are high current, low voltage discharges that occur between cold electrodes at low gas pressures. Processes occurring in the vicinity of the cathode cause the ablation of the cathode surface, producing craters and the formation of a dense hot plasma within 10 m of the cathode surface. These restricted regions that appear and disappear are called cathode spots. The cathode spot plasma is created rapidly by a localized ejection of material from the cathode in a microjet. The plasma is highly dense at this stage and the electrons, at least, are very hot. A high degree of ionization is created by collisions with electrons in the cathode sheath and in the plasma itself and by spontaneous ionization. The cathode spot plasma undergoes a rapid expansion and has a short lifetime of less than 20 ns. Ions are observed streaming away from a cathode spot with surprisingly high kinetic energy, overcoming an externally applied potential with an excess energy in the range 20-100 eV, depending on the cathode material. Cathode spots show a chaotic motion over the cathode surface, with new ones replacing those that extinguish. Ions accelerated towards the cathode may be responsible for the formation of new cathode spots to sustain the discharge.

The cathode spot plasmas have a substructure consisting up to five subspots (fragments) and that subspots themselves have a fine substructure consisting of cells. A cell is believed to be the smallest continuous plasma unit in the discharge. Cells within a subspot have rapidly varying luminosity and appear and disappear rapidly. The substructure gives rise to the non-stationary, repetitive character of cathode spots and to their finite lifetimes. This has led to models that postulate the existence of particle emitting explosive centers on the cathode surface.

MOLECULAR DYNAMICS MODEL

To investigate the processes that occur during the expansion phase of a cathode spot plasma as it expands from its initial high density state, we use a model of a single plasma cell containing a relatively small number of ions of single, multiple or mixed charge states and sufficient electrons to give overall electrical neutrality. In our all particle simulation, the motion of the charged particles is classical and is governed by the Coulomb interactions between all particles.

We model a cathode spot plasma cell as a collection of N charged particles initially within a cube centered at the Origin of a coordinate system. The cell has no net charge. Excitation, ionization and recombination effects are ignored. In the initial state of the plasma, it is assumed that electron-electron collisions are frequent and an electron temperature T_E is already established so that the electrons can be given a Maxwellian velocity distribution. In the case of the ions, the initial velocities are much smaller than those of the electrons because of their much greater mass. So, the initial velocities of the ions are set to zero.

The evolution of a cell is followed using classical dynamics in which the Coulomb interaction gives rise to the forces between the charged particles. The Coulomb force on the i^th particle with charge q_i in the plasma results from the interaction with the other (N-1) particles. The x, y and z components of this force are:

(1)

where e_o is the permittivity of free space and is the displacement vector between the particles i and j with components , and . Since the forces between the charges are conservative, we can define the potential energy of the system U as

(2)

The kinetic energy K and total energy E of the system are given by equations 3 and 4

(3)

(4)

where , and are the mass, velocity and kinetic energy of the i^th particle respectively. Since all the forces acting in the system are conservative, the total energy E is a conserved quantity.

This all particle, N-body problem is difficult to solve numerically because close interactions occur, especially when an electron is trapped by a positive ion, leading to inconveniently large forces. To overcome this problem for close approaches a small constant is introduced such that . To solve the equation of motion, a Velocity-Verlet type integrator was used that gives the positions of all the particles at each time step without calculating any forces, accelerations or velocities. The x coordinate of the i^th particle at time step is given by

(5)

where is the time increment. Similar equations apply for the y and z coordinates. The velocity and kinetic energy of each particle and the potential energy and total energy of the system at any time are calculated from the position of the particles. Extremely small time step in the order of 10^-18 s have to be used for most simulations, otherwise the total energy will not conserved.

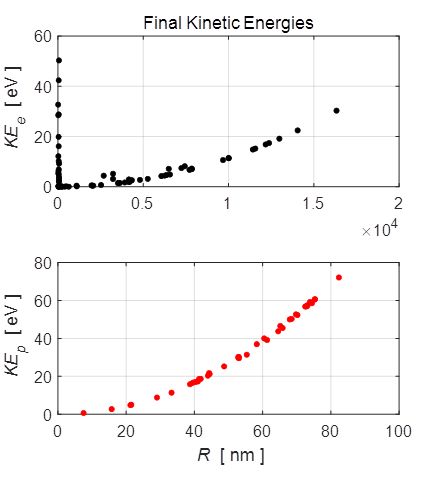
From the observations of running numerous simulations with different input parameters, the following conclusions can be made:

1. A fully ionized cathode plasma cell containing hot electrons undergoes an explosive expansion. Two distinct regions rapidly form, an ion-rich positively charged core and a more rapidly expanding electron halo containing relatively high energy electrons.

2. At the system sizes studied, the electrons are shared in almost equal numbers between the core and the halo. The gain in the kinetic energy of the ions comes from a decrease in the potential energy of the system and a substantial energy transfer from electrons to ions.

3. The final ion kinetic energy is only weakly dependent upon the number of particles in the expanding plasma, essentially independent of the mass of the ions but strongly dependent on the initial density. A weak dependence on initial electron and ion temperatures of the plasma are observed. In the simulation with a large initial density of 2x10²⁹ particle.m^-3, the maximum kinetic energy of an ion is greater than 30 eV. This figure is in reasonable agreement with measured kinetic energy which range from about 20 to 50 eV for single charged ions.

The simulations make an important prediction that does not depend on the assumptions of initial electron temperature, initial system size or initial ion density. The simulations show that on average the higher charged ions always acquire more kinetic energy than the lower charge ions. This prediction is contrary to the interpretation of experiment results made by some authors, but in agreement with most experimental observations.

SIMULATION 1 50 Ti⁺ ions

This simulation with 100 charged particles and 5 million time steps took about 50 minutes and used up lots of memory. The positive ions Ti⁺ correspond to singularly ionized titanium atoms. The number density of the charged particle is very high. However, to get large final values of kinetic energy that agrees with experimental measurements, one must use a large initial number density. By observing the following table and plots you can account for the increase in ion kinetic energy as due to the decrease in kinetic energy of the electrons and the decrease in potential energies due to the electron-electron and positive ion–positive ion interactions.

Table 1. Summary of simulation input and output parameters for Ti⁺.

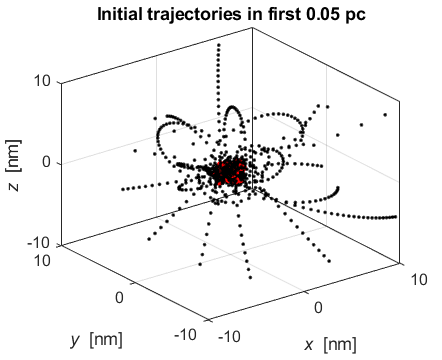
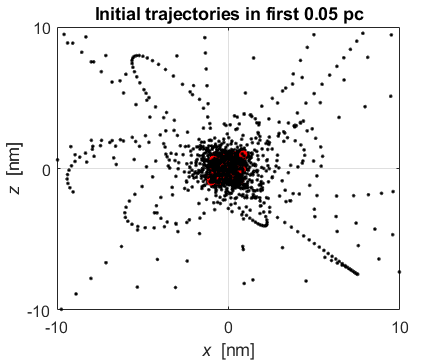
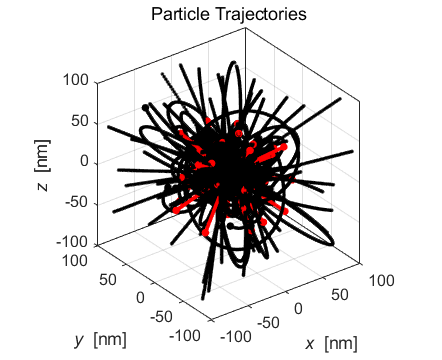
Fig. 1A. The trajectories of the charged particles near the Origin at the beginning stages of the explosion. The positive ions are grouped closer to the Origin than the electrons. Many electrons move in complicated orbits within the positive core while other electrons escape from the core region.

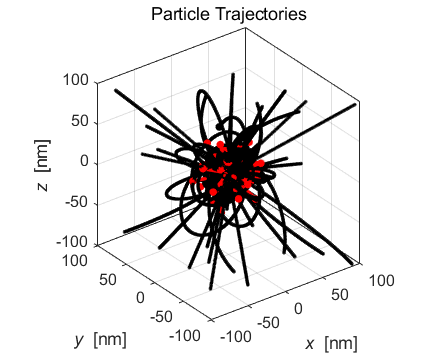
Fig. 1B. The trajectories of the charged particles. The positive ions are still grouped relatively close to the Origin. About 50% of the electrons have not travelled great distances from the Origin and they move in complicated orbits about the positive ions in this core region. The other 50% of the electrons form a halo region surrounding the positive core. Many of the escaped electrons are at great distances from the core at the end of the simulation.

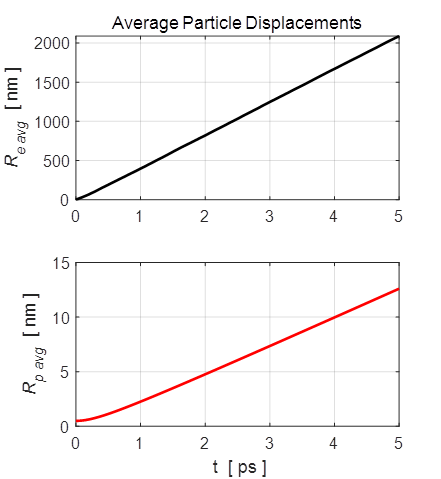
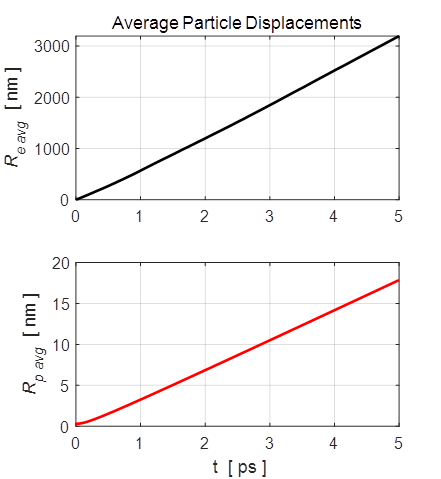
Fig. 2. The electrons on average are displaced through much larger distances from the Origin than the positive ions because of their much smaller mass. The average expansion for the both electrons and positive ions is approximately uniform. The more energetic a positive ion then the more likely for it to be located further from the Origin. This not necessarily the case with the electrons. The electrons can be divided into two distinct groups. The electrons with the core region of the expansion and basically are bound to the positive ions and the other group forming a halo region surrounding the core of net positive charge. The overall positive charge of the core drives the continual expansion of the cell.

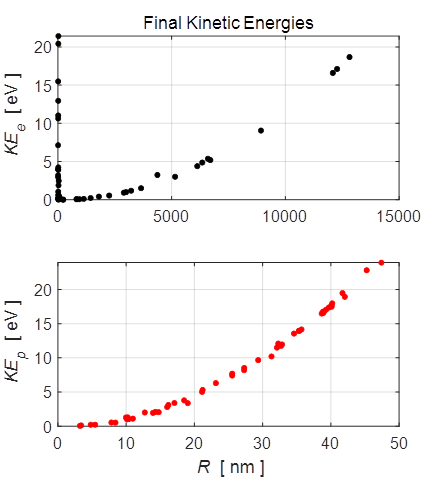
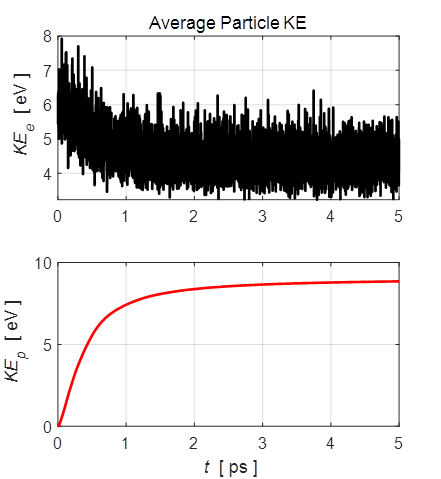
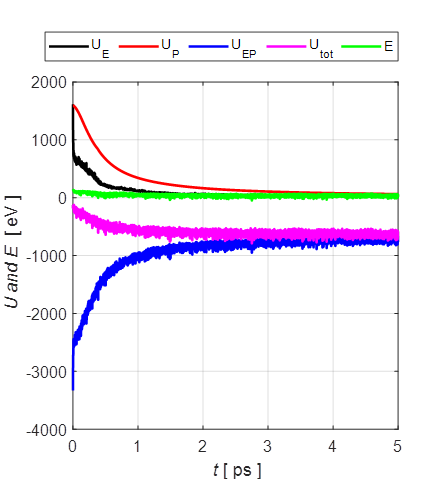
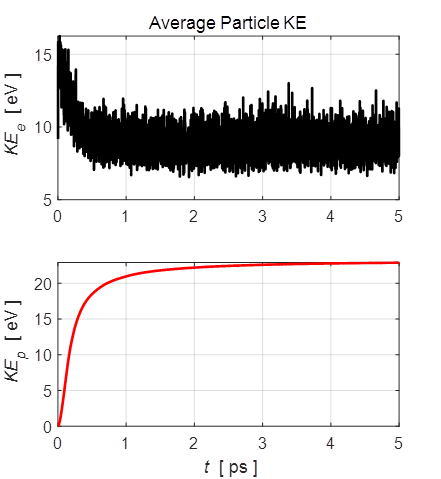
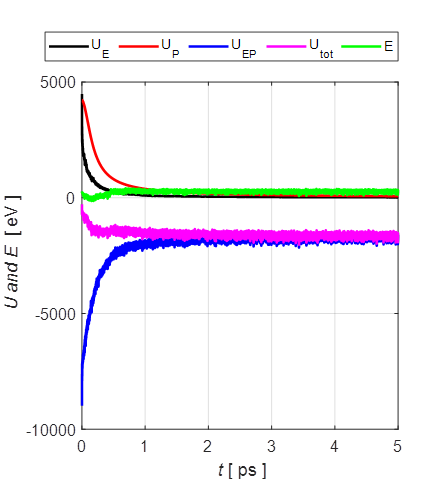
Fig. 3. A typical evolution of the average kinetic energies of the electrons and positive ions. When the charged particles are sufficiently far from each other, the Coulomb interaction forces between the charged particles are small and which results in an almost steady state value for the average kinetic energy of the positive ions in the later stages of the expansion of the plasma.

The potential energy of the system U has three contributions from interactions between the charged particles as shown in figure 4.

1. A positive contribution for the interaction between electrons U_E (U₁).

2. A positive contribution for the interaction between the positive ions U_P (U₂).

3. A negative contribution for interactions between electrons and ions U_PE (U₁₂).

Initially, all the particles are close to each other and so there are large positive and large negative contributions to the potential energy that are approximately equal, resulting in a small negative value for the total potential energy of the system. At the end of a simulation, the average distances between the charges are much greater and the magnitudes of all three contributions to the potential energy decrease. This results in the final potential energy being more negative than the initial value. This decrease in potential energy accounts for some, but not the majority, of the kinetic energy gained by the ions.

Fig. 4. Typical time evolution of the potential energies of the system. U_E is potential energy for the electron-electron interaction; U_P is the ion-ion interaction; U_EP is the electron-ion interaction; U_tot is the sum of the potential energies due to the three interactions; and E is the total energy of the system. In the simulation, the total energy is approximately conserved. Deviations from energy conservation can occur due to the close encounters of the charged particles with each other.

The measured average Ti⁺ kinetic energies are about 60 eV. The maximum kinetic energies of the ions in the simulation were about 25 eV. The input parameters could be changed to see if a better agreement can be reached.

SIMULATION 2 T²⁺

Table 1. Summary of simulation input and output parameters for Ti⁺⁺. The doubly charged titanium ions are considerably more energetic than the plasma contained singularly charged titanium ions.

Ti⁺ K_Pavg = 8.9 eV K_Pmax = 23.9 eV

Ti²⁺ K_Pavg = 34.4 eV K_Pmax = 72.1 eV

Fig. 5A. The trajectories of the charged particles near the Origin at the beginning stages of the explosion. The positive ions are grouped closer to the Origin than the electrons. Many electrons move in complicated orbits within the positive core while other electrons escape from the core region.

Fig. 5B. The trajectories of the charged particles. The positive ions are still grouped relatively close to the Origin. About 50% of the electrons have not travelled great distances from the Origin and they move in complicated orbits about the positive ions in this core region. The other 50% of the electrons form a halo region surrounding the positive core. Many of the escaped electrons are at great distances from the core at the end of the simulation.

Fig. 6. The electrons on average are displaced through much larger distances from the Origin than the positive ions because of their much smaller mass. The average expansion for the both electrons and positive ions is approximately uniform. The more energetic a positive ion then the more likely for it to be located further from the Origin. This not necessarily the case with the electrons. The electrons can be divided into two distinct groups. The electrons with the core region of the expansion and basically are bound to the positive ions and the other group forming a halo region surrounding the core of net positive charge. The overall positive charge of the core drives the continual expansion of the cell. Note: many of the electrons within the core region have large values for their kinetic energies.

Fig. 7. A typical evolution of the average kinetic energies of the electrons and positive ions. When the charged particles are sufficiently far from each other, the Coulomb interaction forces between the charged particles are small and which results in an almost steady state value for the average kinetic energy of the positive ions in the later stages of the expansion of the plasma.

Fig. 8. Typical time evolution of the potential energies of the system. U_E is potential energy for the electron-electron interaction; U_P is the ion-ion interaction; U_EP is the electron-ion interaction; U_tot is the sum of the potential energies due to the three interactions; and E is the total energy of the system. In the simulation, the total energy is approximately conserved. Deviations from energy conservation can occur due to the close encounters of the charged particles with each other.