|
|
IZHIKEVICH MODEL FOR
NETWORKS OF COUPLED NEURONS |
|
ns_Izh022.m
Computation of the membrane potential activity for a sparse network of
randomly coupled neutrons ns_IZH_N012.m
[2D] Neural network with Mexican hat coupling function |
|
|
The
Izhikevich model for a neuron can be used to
simulate a sparse network of 103 spiking cortical neurons with 106
synaptic connections. Based upon the anatomy of a mammalian cortex, ratio of
excitatory to inhibitory neurons is taken to be 4 to 1 with inhibitory
synaptic connections stronger than the excitatory synaptic connections. Also,
each neuron receives a noisy thalamic input (presynaptic input into areas of
the cerebral cortex from the thalamus). All neurons have different dynamics
for heterogeneity. This is done by assigning to each neuron a range of values
for the parameters a,
b, c
and d using the uniformly distributed variables re and ri
which vary from 0 to 1. The time evolution of the membrane potential
v is described in terms of the differential
equations (1)
(2) The
after-spike resetting relationship is (3) where u
is the membrane recovery variable. The dimensions and values of the model
parameters are v
membrane potential
[mV] t time [ms] dv/dt time rate of change
in membrane potential
[mV.ms-1 or V.s-1] u
recovery variable [mV] I external
current input to cell (synaptic currents or injected DC-currents) [A] c1 = 0.04 mV‑1.ms-1 c2 = 5 ms-1 c3 = 140 mV.ms-1 c4 = 1 ms-1 c5 = 1 [mV.ms-1.A-1 Ω.ms-1] Excitatory
cells (variations in c and d) Regular
spiking cells a = 0.02 b = 0.20 c = -65 d = 8 Chattering
cells
a = 0.02 b = 0.20 c = -50 d = 2
c = - 65 + 15 re2 d = 8 – 6 re2 re = 0 corresponds to regular spiking
cell re = 1 corresponds to the chattering
cell re2 used to bias the distribution toward
regular spiking cells. Inhibitory
cells (variations in a and b)
Fast Spiking cells a = 0.02 + 0.08 ri
b = 0.25 - 0.05 ri c = -65 d = 2 |
|
Part of the mscript ns_Izh022.m for simulation of mammalian cortex network % INPUT PARAMETERS =============================================== Ne = 800; Ni = 200;
% number of excitatory & inhibitory
neurons Nt =
1000;
% number of time steps numE =
10; numI = Ne + 10;
% indices for one excitatory and one
inhibitory neuron % Model parameters
=============================================== re = rand(Ne,1); ri = rand(Ni,1); % random numbers a = [0.02 * ones(Ne,1); 0.02 +
0.08*ri]; b = [0.20 *ones(Ne,1); 0.25 - 0.05*ri]; c = [-65+15*re.^2;
-65*ones(Ni,1)]; d = [8-6*re.^2 ; 2*ones(Ni,1)]; S = [0.53*rand(Ne+Ni,Ne), -rand(Ne+Ni,Ni)];
% coupling strengths v = -65*ones(Ne+Ni,1); % Initial values of v u = b.*v; % Initial values of u firings = [];
% spike timings vE =
zeros(Nt,1); vI = zeros(Nt,1);
% membrane potential of 2 neurons % Time Evolution of Systems
======================================= for t = 1:Nt I = [5*randn(Ne,1);2*randn(Ni,1)]; % thalamic
input fired = find(v>=30);
% indices of spikes firings = [firings; t+0*fired,fired];
% time steps / fired neurons v(fired) = c(fired);
% membrane potential u(fired) =
u(fired)+d(fired); % recovery potential I = I+sum(S(:,fired),2);
% thalamic + synaptic input v =
v+0.5*(0.04*v.^2+5*v+140-u+I); % HALF-STEP:
step 0.5 ms v =
v+0.5*(0.04*v.^2+5*v+140-u+I); % for numerical stability u = u+a.*(b.*v-u);
vE(t) = v(numE);
% excitatory neuron
vI(t) = v(numI);
% inhibitory neuron end; vE(vE > 30) = 30; vI(vI > 30) = 30; tS = 1:Nt; nF = zeros(Nt,1); % fired neurons at each time step for t = 1 : Nt nF(t)
= sum((firings(:,1) == t)); end |
|
The
model belongs to the class of pulse-coupled neural networks (PCNN) where the synaptic connection weights between the
neurons are given by the matrix S so
that firing of the nth
neuron instantaneously changes membrane potential variable vm by S(m, n). |
|
|
|
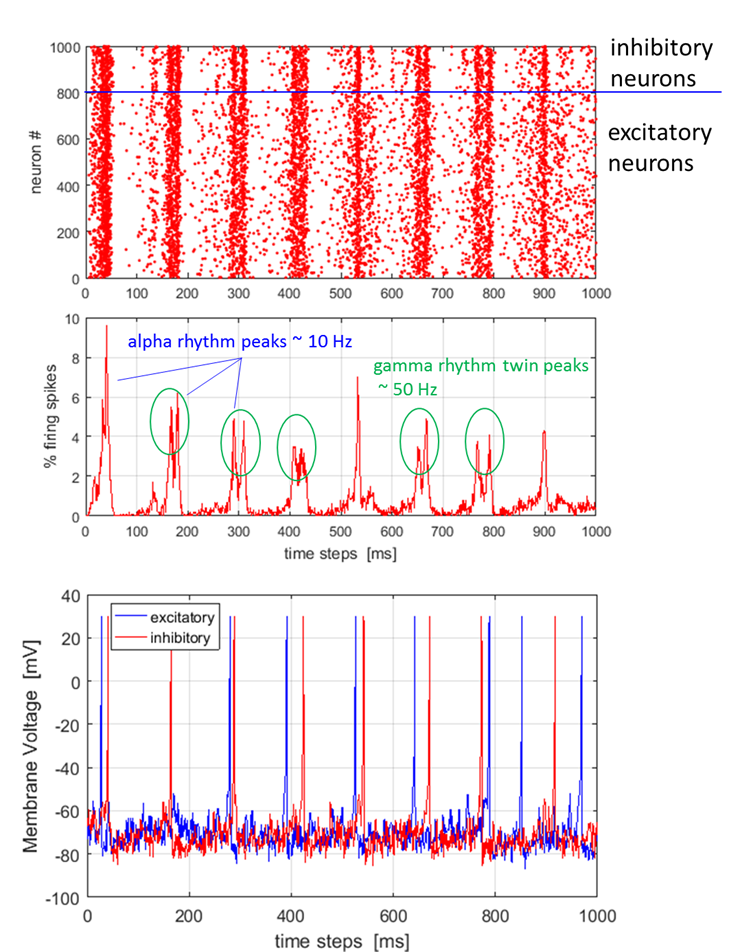
Fig. 1. Network of 103 randomly coupled
spiking neurons (800 excitatory and 200 inhibitory) with 106
synaptic connections. Top: spike-train raster plot shows episodes of alpha rhythms (single widely spaced peaks) and gamma band rhythms (double closely spaced
peaks). Bottom: Typical spiking activity of an excitatory neuron and an
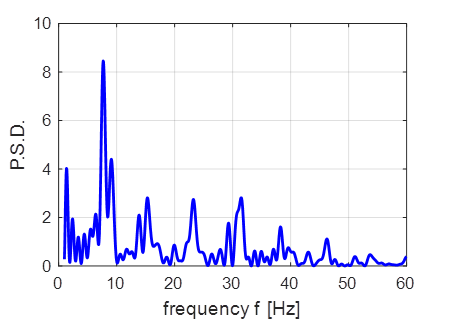
inhibitory neuron (peaks normalized to +30 mV). The Foureir transform of the number of
firings at each time step is shown in figure 2. Figure 2 shows a distinct each near 8 Hz which may correspond to the
episodes of the alpha rhythms. Howver, the Fourier transform does not
indicate the gamma rythym oscillations.
Fig. 2. Fourier trnasform of the number
of firings at each time step. |
|
|
|
Neural activity in the neocortex
is highly irregular and the origin of this irregular activity may be in the
tight balance between excitatory and inhibitory synaptic inputs. Highly
fluctuating net input currents whose means are below threshold results in
action potentials being generated by the fluctuations. Neural activity in
this state is chaotic in the sense that slight changes in initial conditions
leads to drastically different patterns of spike times. The network of
neurons in the asynchronous state displays activity that looks random where
the firing rate at which action potentials are
emitted stochastically. Figure 1 shows that the network exhibits
cortical-like asynchronous dynamics (neurons fire Poisson spike trains:
excitatory neuron firing rate ~ 7 Hz and inhibitory firing rate ~ 8
Hz). The neurons self-organize into assemblies in which different neurons
asynchronously emit action potentials and they exhibit collective rhythmic
behaviour in the frequency range corresponding to that of the mammalian
cortex in the awake state and although the network is connected randomly and
there is no synaptic plasticity. The alpha rhythm
corresponds to the normal bursts of electrical activity within the
frequency range from 8 to 13 Hz in the cerebral cortex of a drowsy or
inactive person. The gamma rhythm is the
burst of electrical activity at higher frequencies than the alpha rhythm
within a frequency between 25 and 100 Hz with 40 Hz a typical value. The Izhikevich model may show some evidence of these rhythms.
The dark red vertical lines in figure 7 (top diagram) indicate that there are
occasional episodes of synchronized firings where single peaks show alpha
rhythm (~10 Hz) and double peaks show the gamma rhythm (~50 Hz). Ostojic concluded from his modelling of sparsely
connected network of spiking neurons of excitatory and inhibitory leaky
integrate-and-fire (LIF) neurons that they can
display two different types of asynchronous activity when at rest: ·
For weak overall synaptic couplings and/or strong inhibition,
the network is in the well-known asynchronous state, in which individual
neurons fire irregularly at rates that are constant in time. ·
For overall synaptic couplings that are strong and/or inhibition
is just strong enough to balance excitation, a new type of resting state emerges.
In that state the neurons still fire irregularly and asynchronously, but the
firing rates of individual neurons fluctuate strongly in time and across
neurons. This new state is called the heterogeneous asynchronous state. Ostojic: “The
two regimes of spontaneous asynchronous activity have different computational
properties, as seen in their responses to temporally varying inputs. In the
classical asynchronous state, the responses of different neurons are highly
redundant, which favors a reliable transmission of
information but limits the capacity of the network to perform nonlinear
computations on the stimuli. In the heterogeneous asynchronous state, the
responses of different neurons to the input instead strongly vary. This
variability in the population degrades the transmission of information but
provides a rich substrate for a nonlinear processing of the stimuli, as
performed, for instance, in decision-making and categorization.” Using the mscript nsIzh022.m, you could investigate other types of
collective behaviour such as spindle waves ? and sleep oscillations ? by
changing the relative strength of synaptic connections and the strength of
the thalamic input. Also, you could verify the findings made by Ostojic using the Izhikevich
model rather than the leaky integrate-and-fire model. I
am not sure how useful is this model is because the model is sensitive to the
model parameters and it is difficult to judge what parameter values to use. |
|
Izhikkevich Quadratic
Model: [2D] NEURAL NETWORK WITH MEXICAN HAT
COUPLING FUNCTION We can simulation the generation of spiking neuron pattern
formations called clusters and
their propagation characteristics using the Izhikevich Quadratic Model for Spiking Neurons using a [2D] square lattice of N x N uniformly
spaced neurons. The time evolution of the membrane potential for each neuron
is calculated using a Mexican-Hat function for the coupling between neurons. ns_IZH_N012.m |
|
Parameters: % Number of N x N lattice elements N = 100; % Number of time steps NT = 200; % Izhikevich Model
parameters C = 50;
vr = -60; vt = -40; k =
0.7; a =
0.01; b = 5; c = -55; d = 150; vPeak = 35; Sext =
20; % Coupling Strength function CE = 0.4; CI = 0.1; dE = 14; dI = 42; dM = 15; d0 = 5.4; WE =
8000; WI =
-8000; |
|
|
|
|
|
|
|
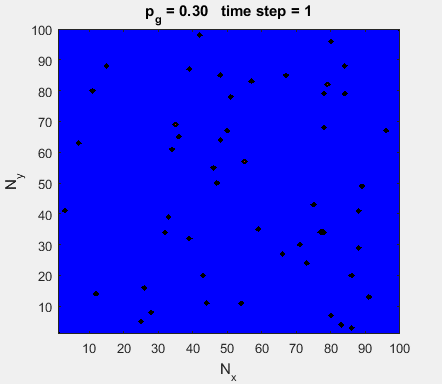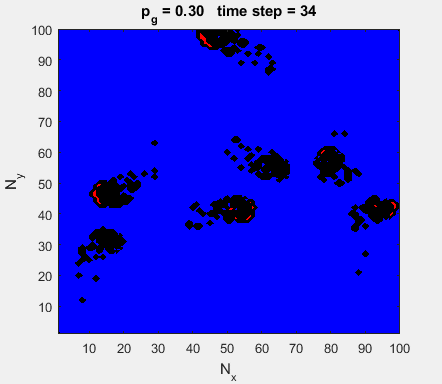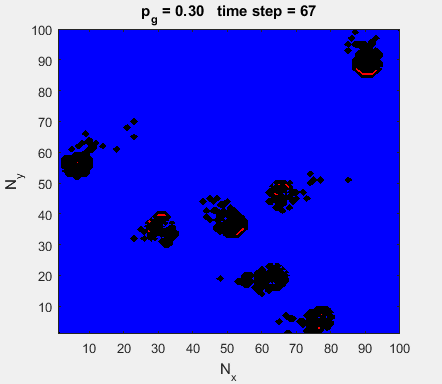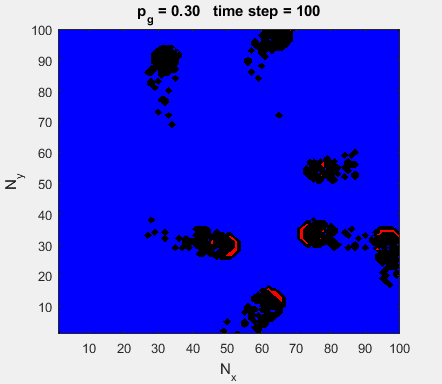
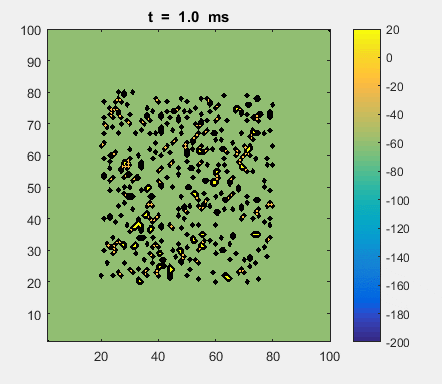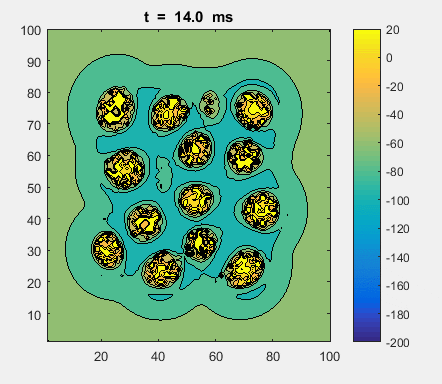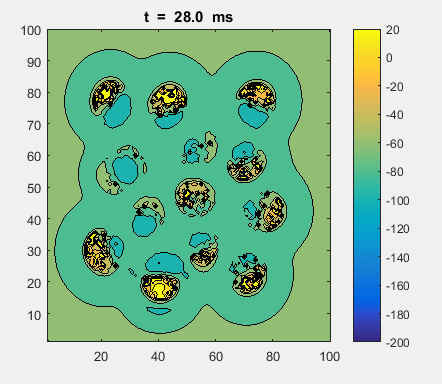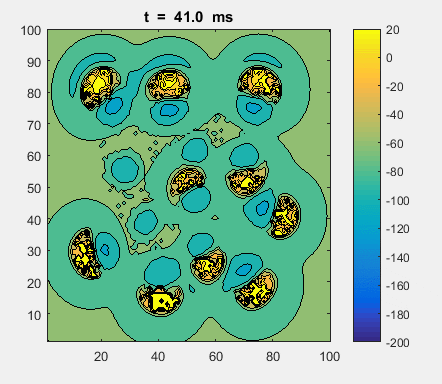
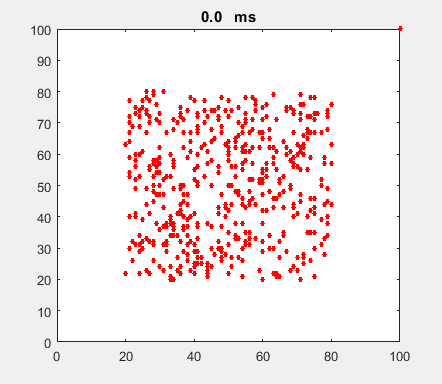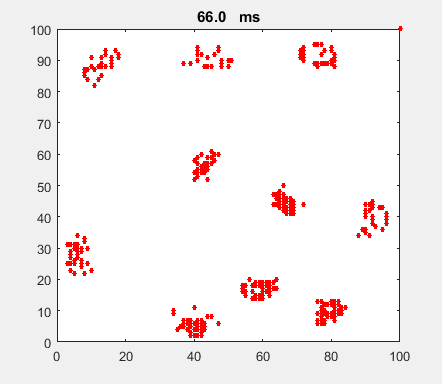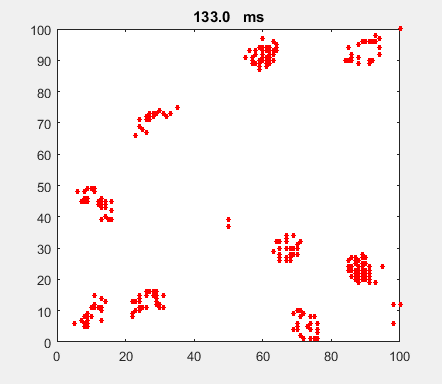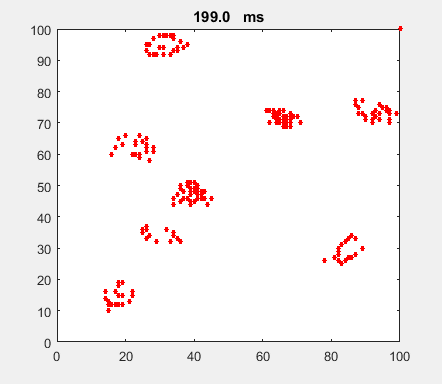
Fig. 4a. Animation of of the
time evolution of the membrane potential. contourf plot (left) of membrane
potential and plot of spiking neurons (right). ns_IZH_N012.m |
|
|
Difficult to know what parameters to use. Need extremely large value
values for Mexican Hat Function parameters WE and WI. Can get wobbling cluster formations but as
yet could not simulate propagating clusters. |
|
|
|
|
|
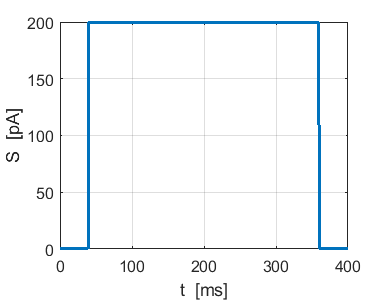
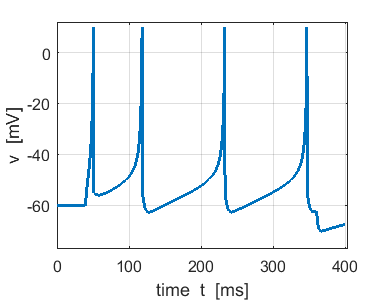
Fig. 4b. Single neuron with
the same Izhikevich paramters used for the simulation shown in figure
4a. ns_Izh_006.m |
|
|
|
|