|
NUMERICAL ANAYSIS OF OPTICAL AND ELECTROMAGNETIC PHENOMENA: THE
VECTORIAL NATURE OF LIGHT: POLARIZATION
cemPol1.m Animated Lissajous figures for the polarization of light as a function of relative phase for orthogonal vibrations of the electric field. The animation of the time evolution of the electric field vector can be saved as an animated gif (flagA = 1) or as an avi file (flagA = 2) or not saved (flagA = 0). The script calls the function arrow.m (downloaded from the Matlab File Exchange). The arrow.m function is a very useful function for adding arrows to your plots.
cemPol2.m (avi) cemPol3.m (gif)
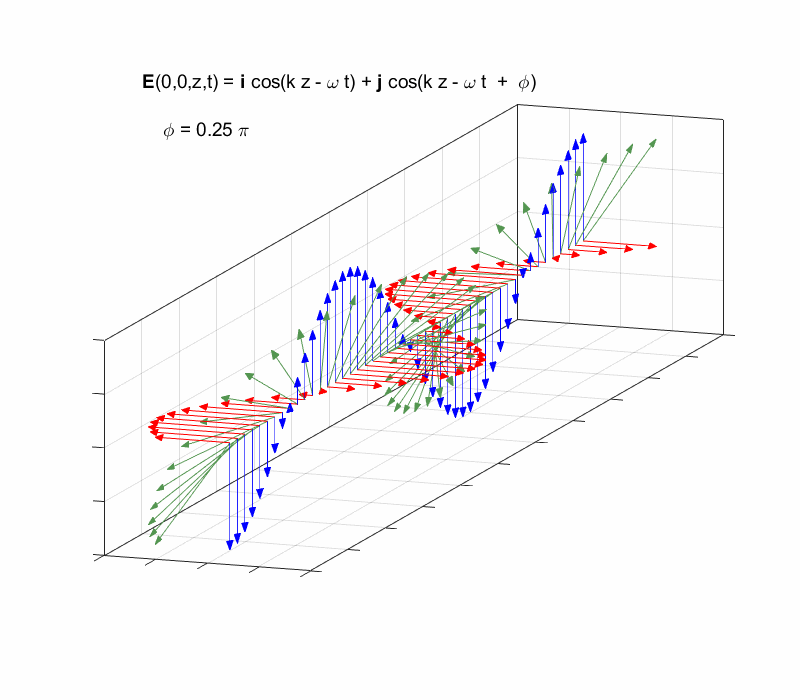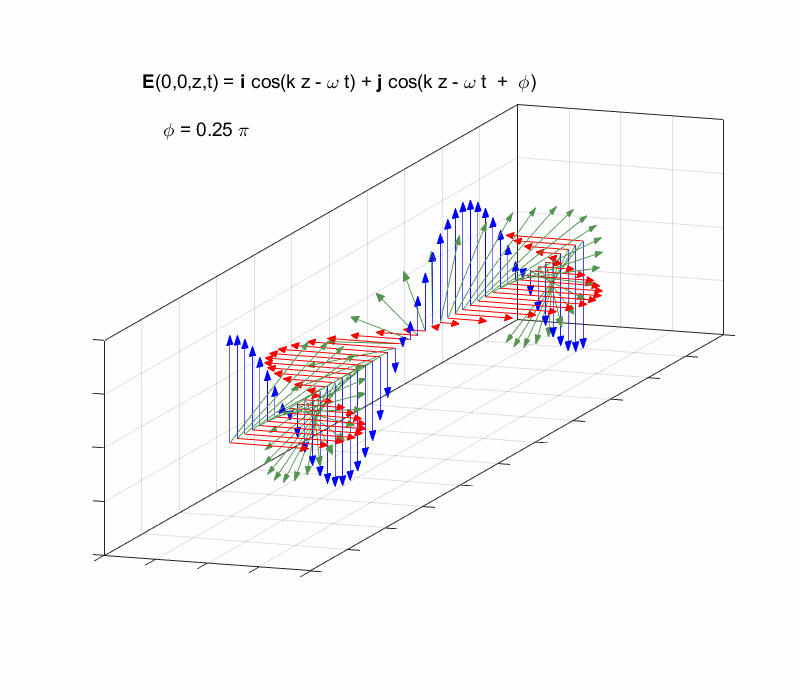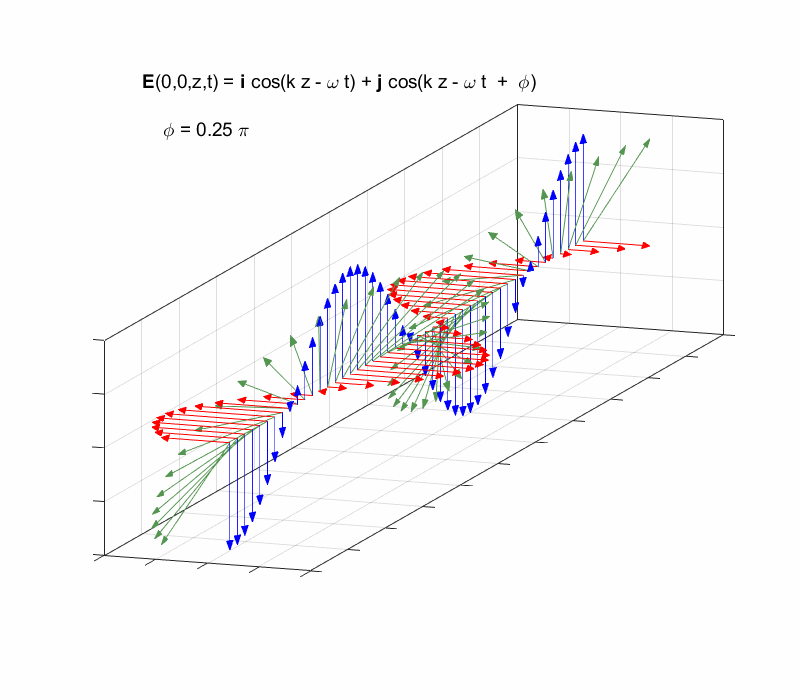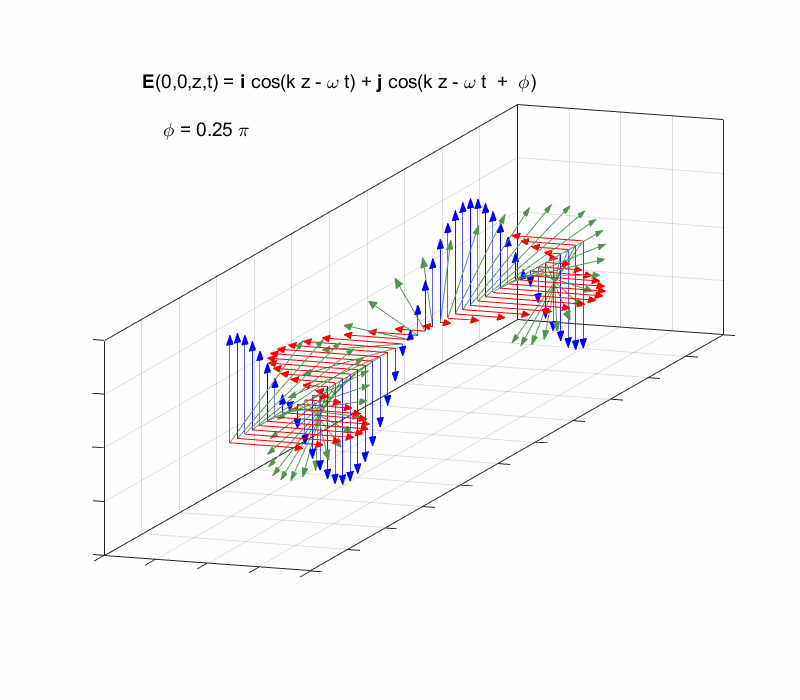
[3D] animation of a travelling elliptical polarized wave propagating
in the Z direction.
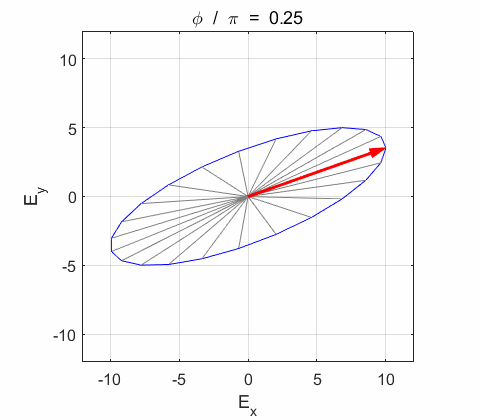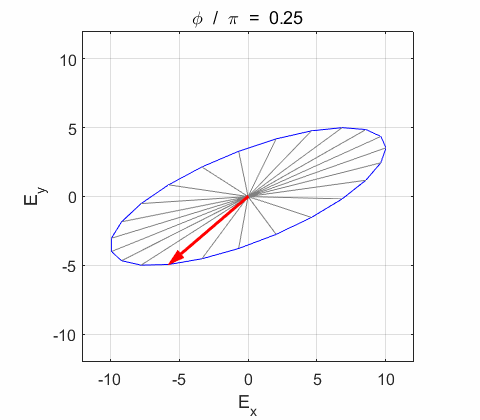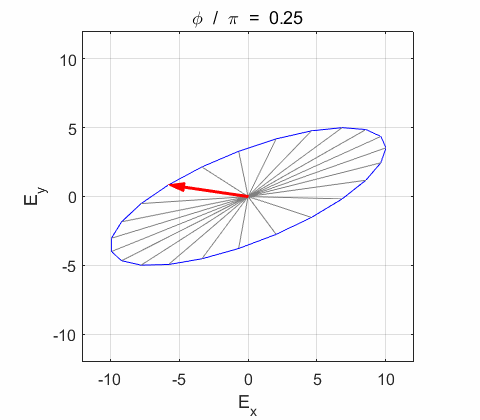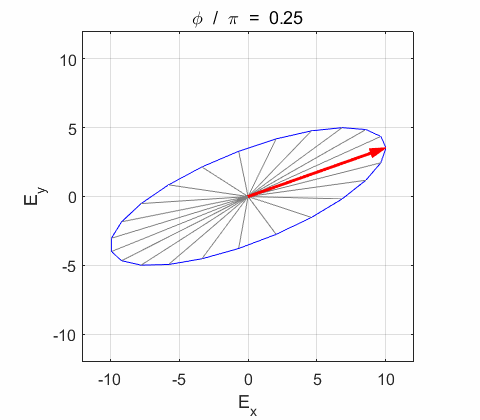
Any state of polarization in a ray of light can be described in terms of elementary components of plane-polarized light. A polarized wave propagating along the Z axis of an orthogonal system of axes maybe analysed in terms of components along the X and Y axes. The two components can be expressed as complex exponential functions.
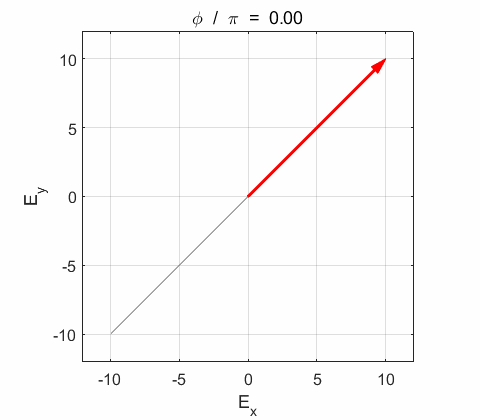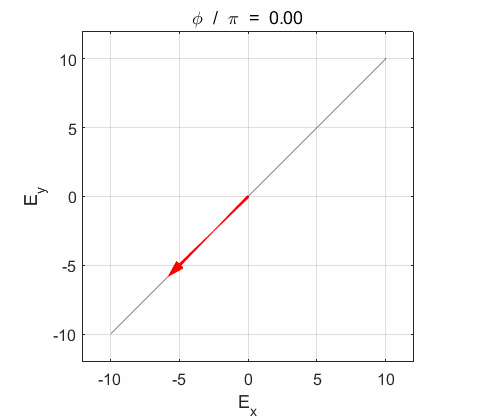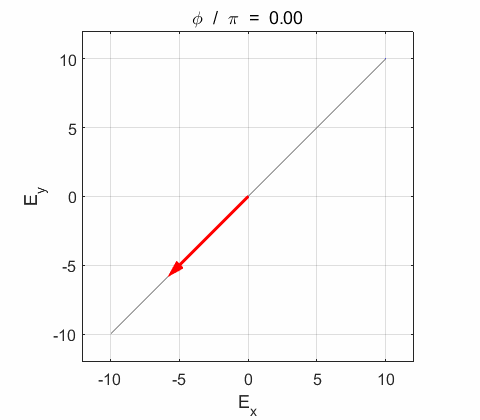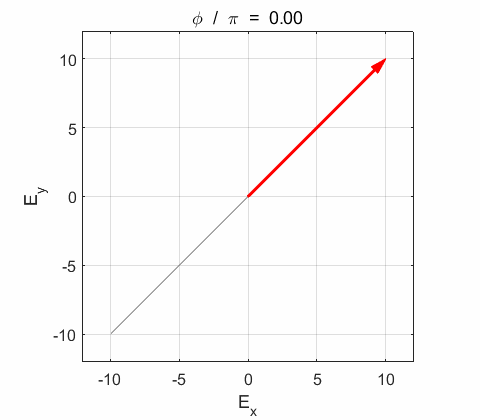
where The actual values for the electric field and its components are given by the real of the complex functions. Phase difference The X and
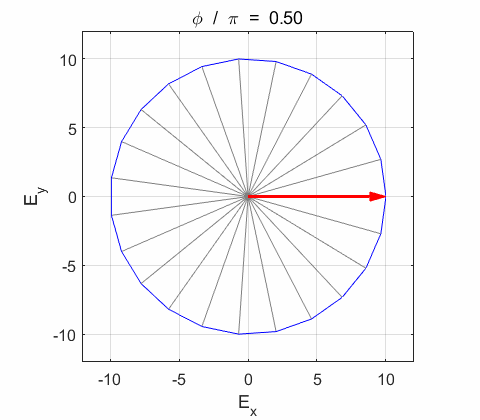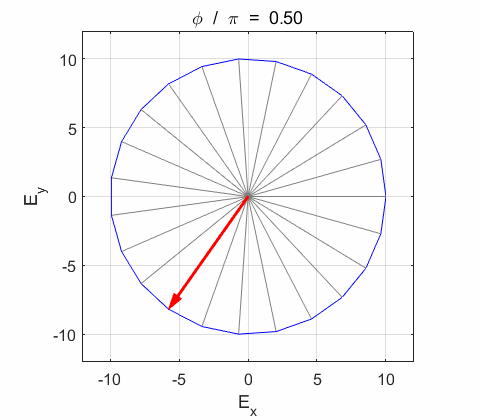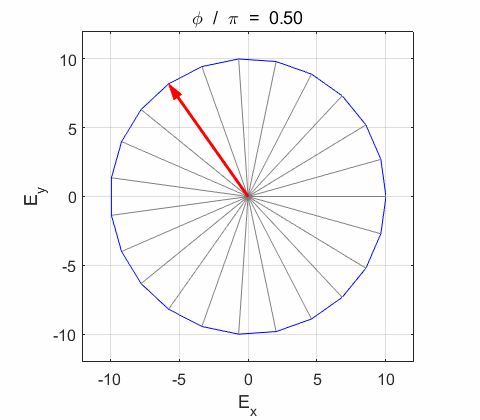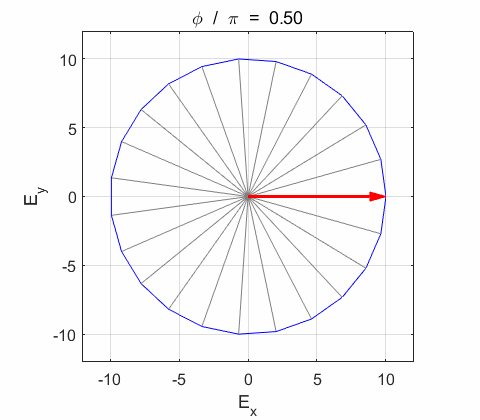
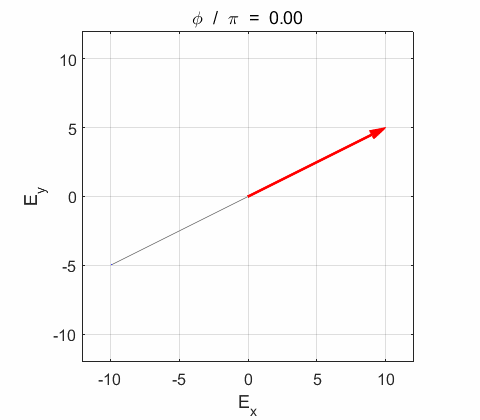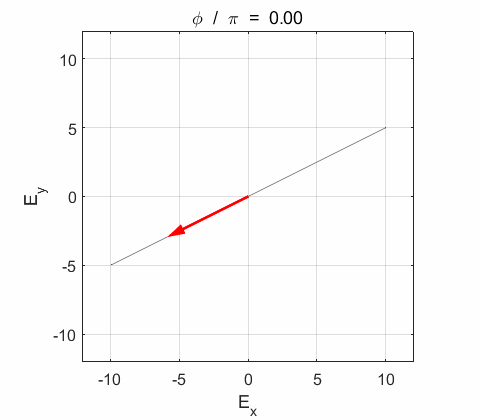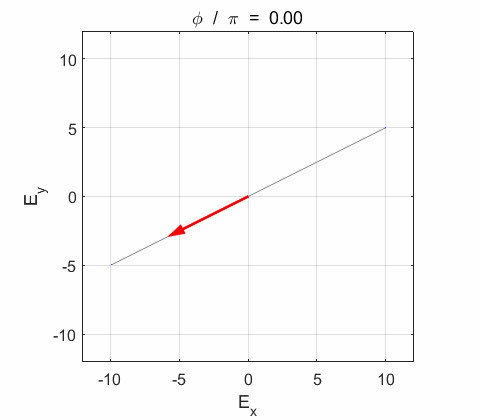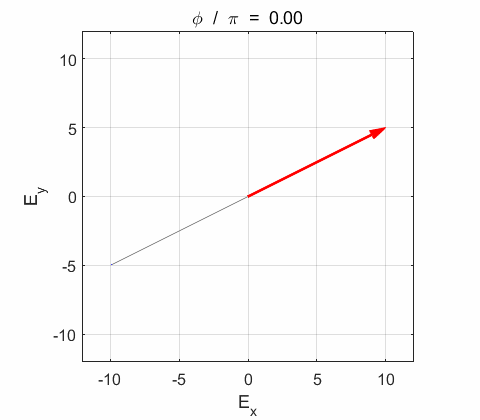
Y components of the wave vibrate in phase. The resultant electric field
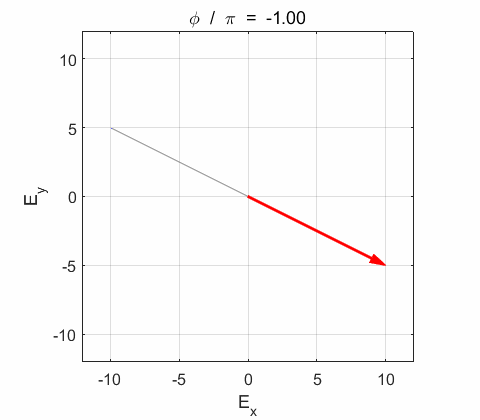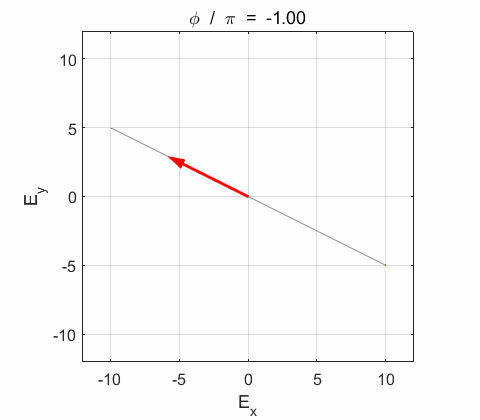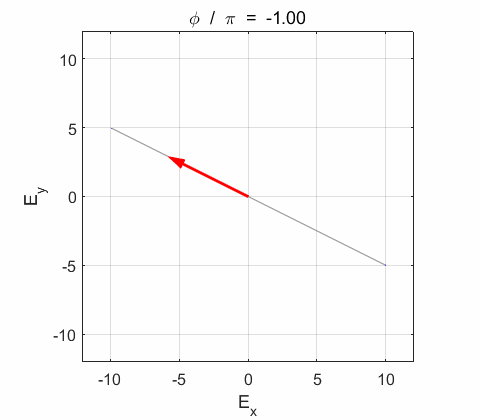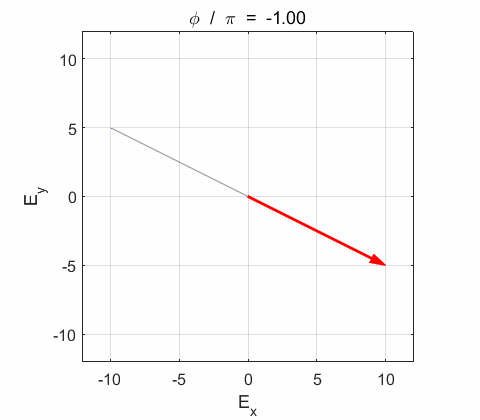
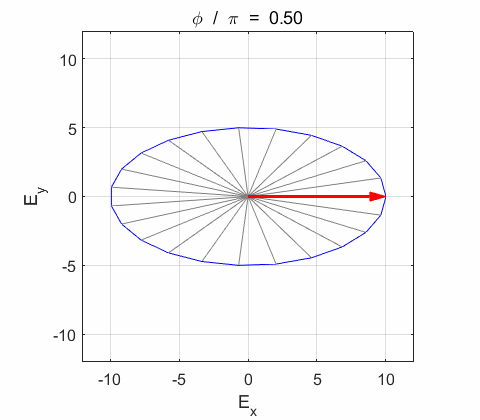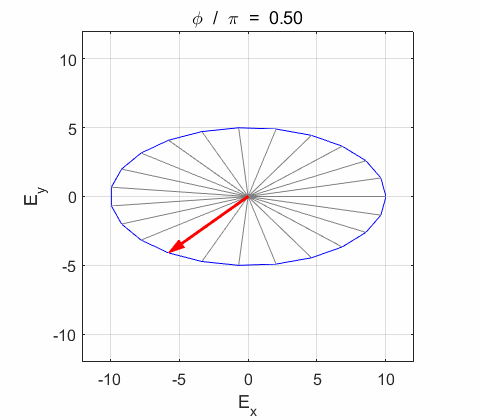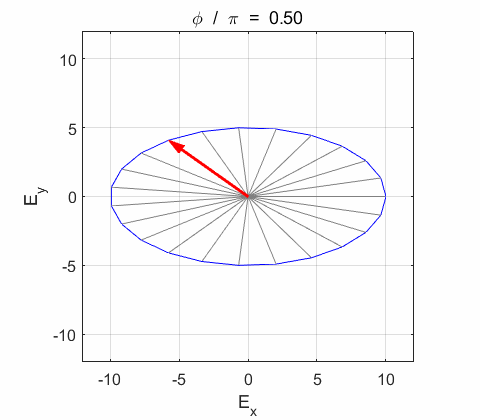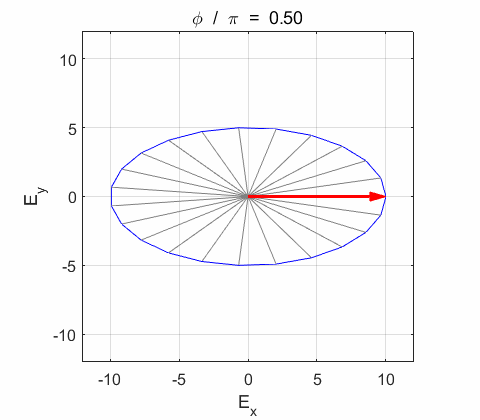
Phase difference
The
resultant electric field
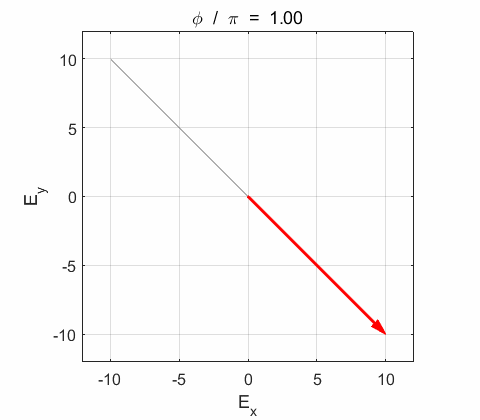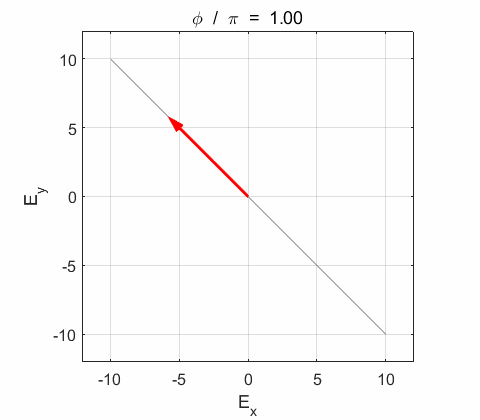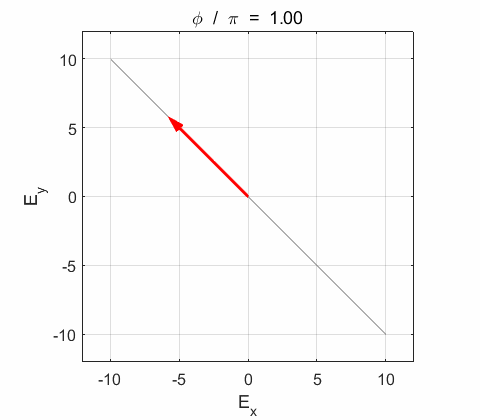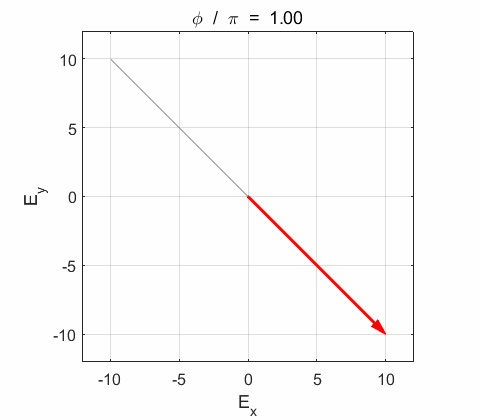
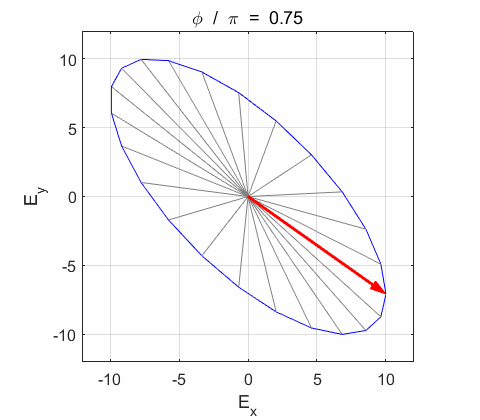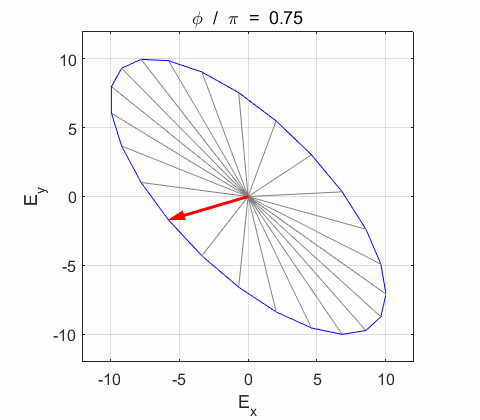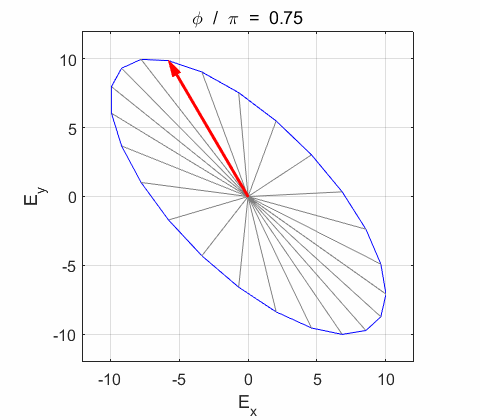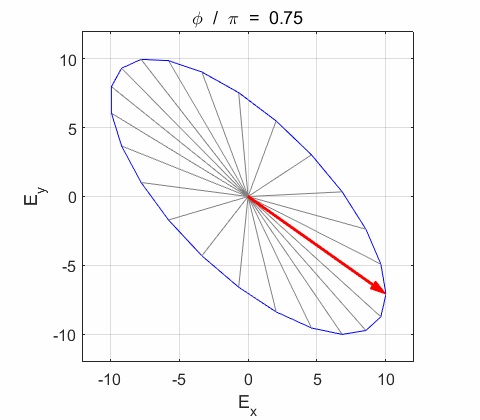
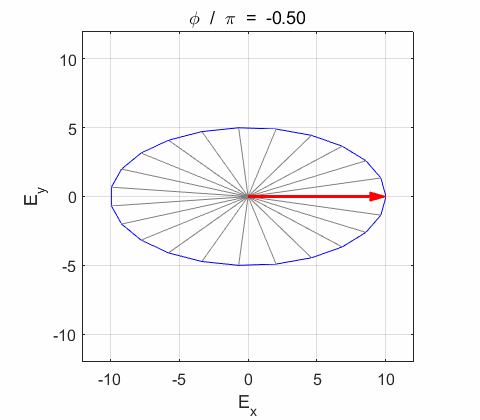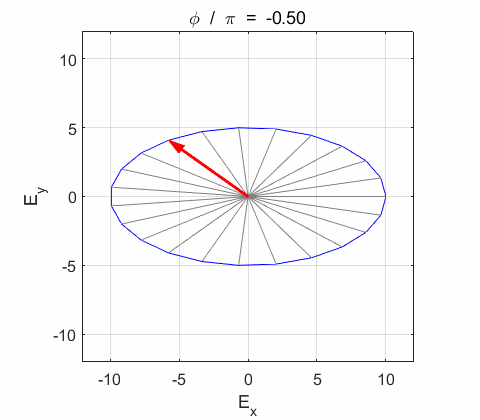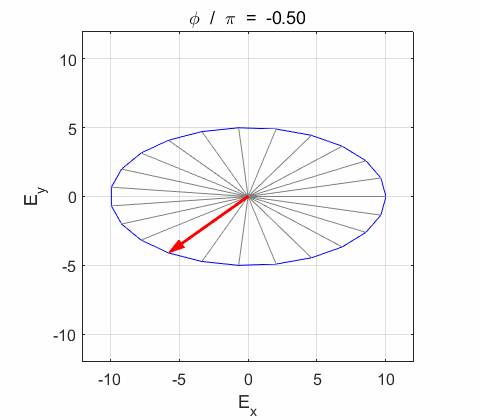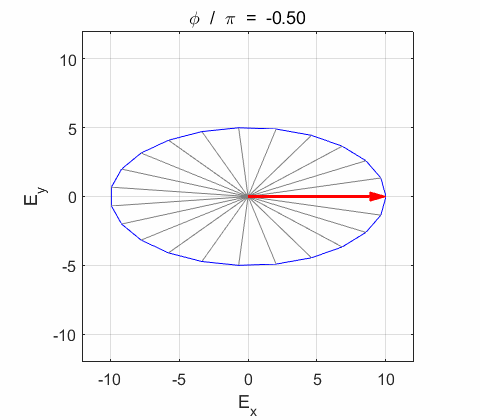
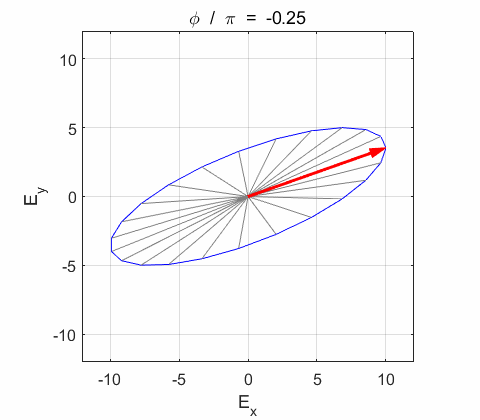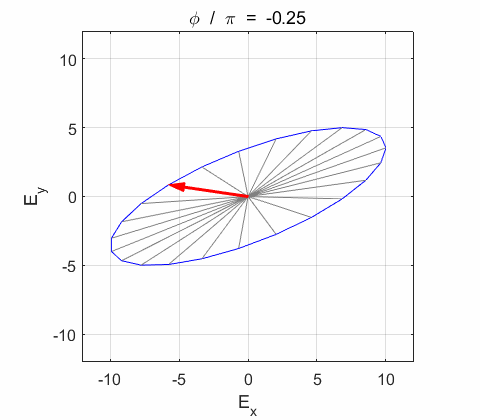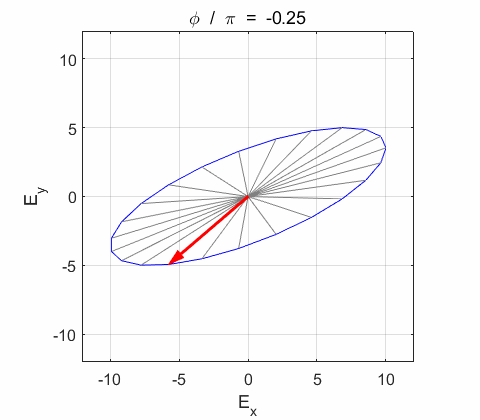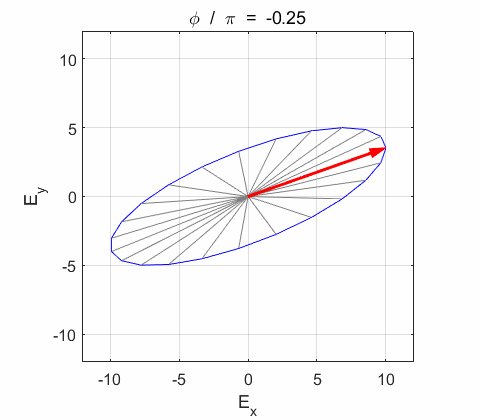
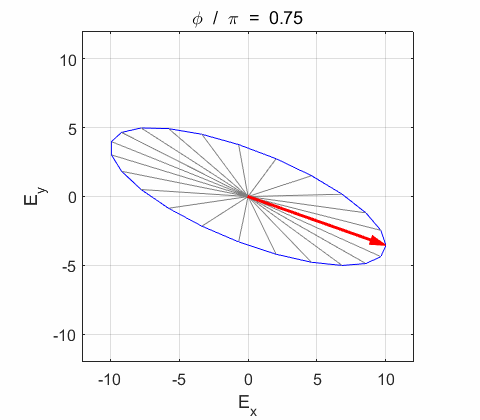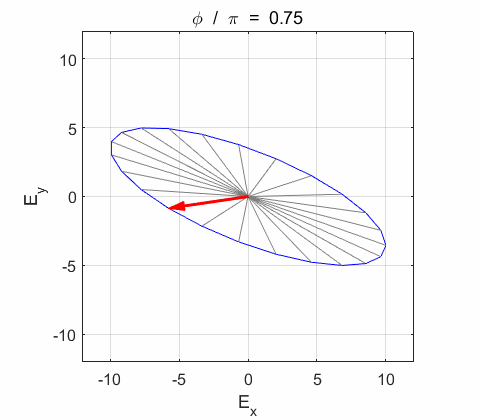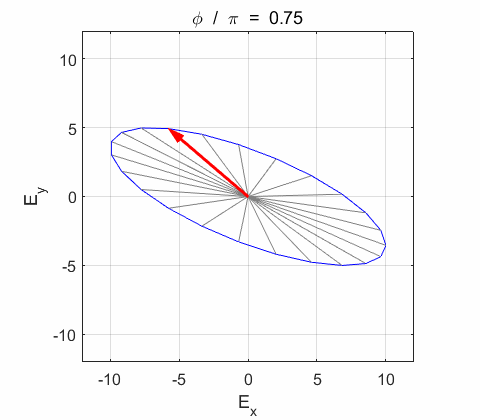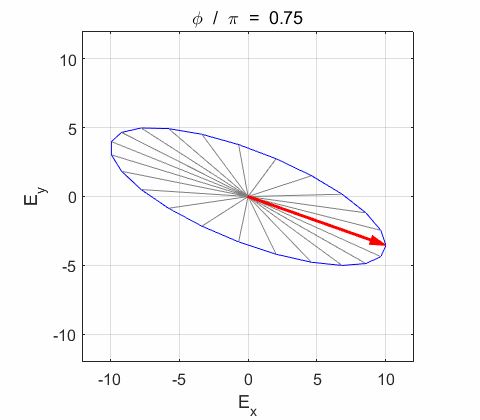
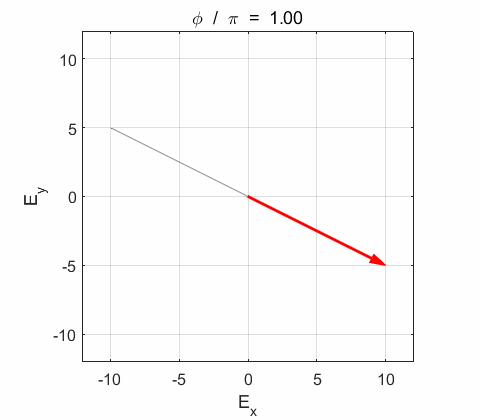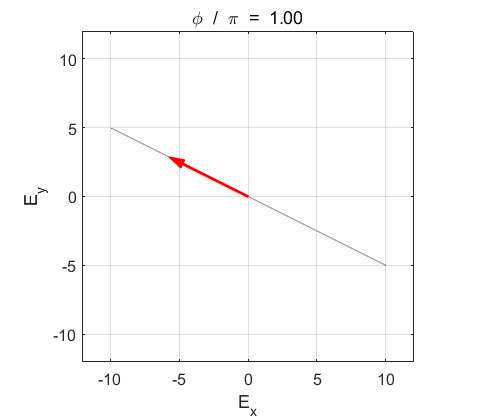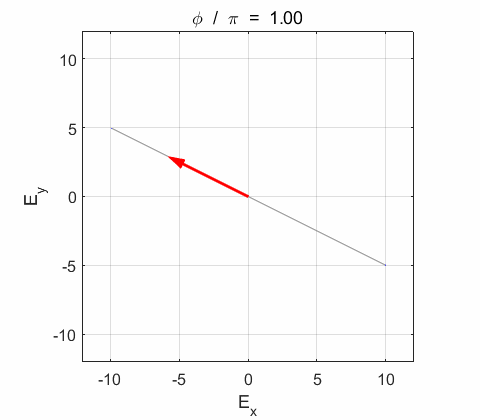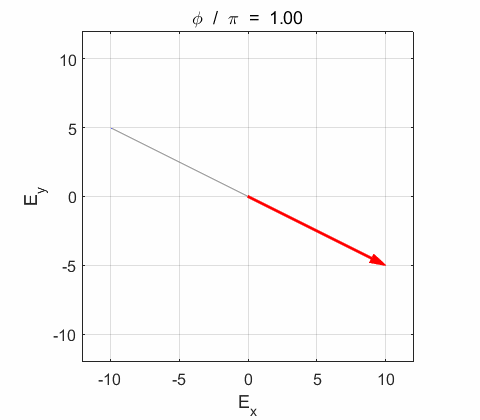
Phase difference The
resultant electric field
The We can
view the elliptical polarized wave propagating along the Z direction in [3D]
using the scripts cemPol2.m (avi) or cemPol3.m (gif). The
gif animation shows the X and Y components and the resultant electric field
for points along the Z axis as functions of time when the phase of the Y
components lead the X components by
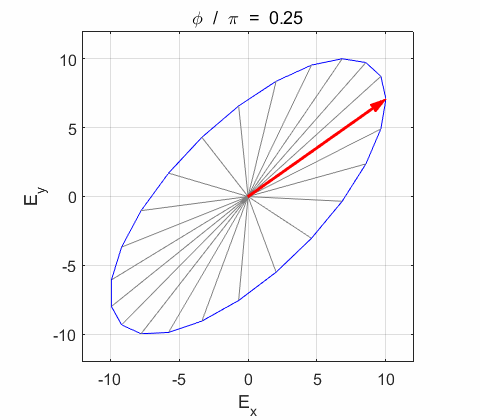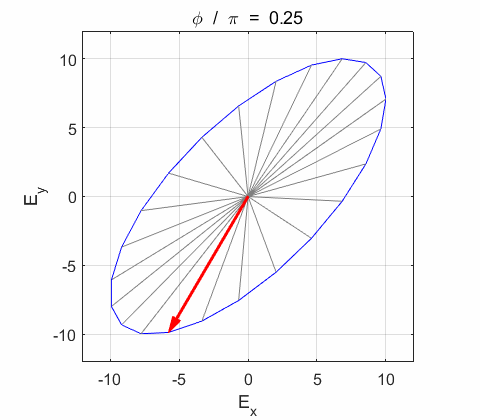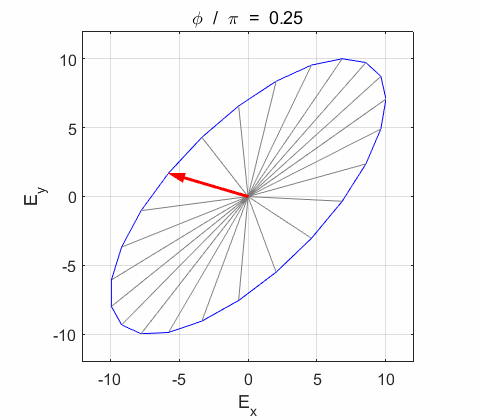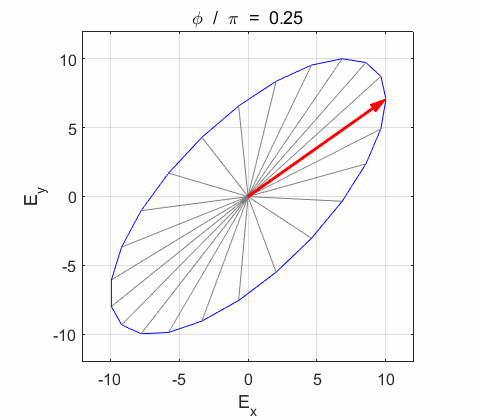
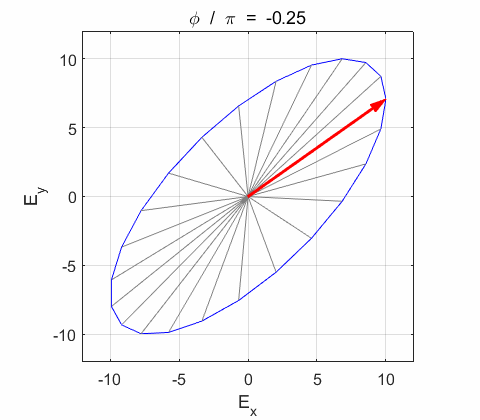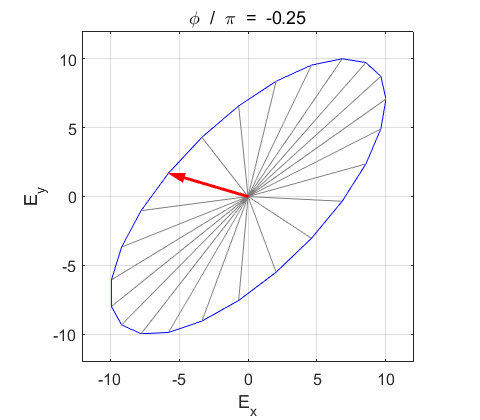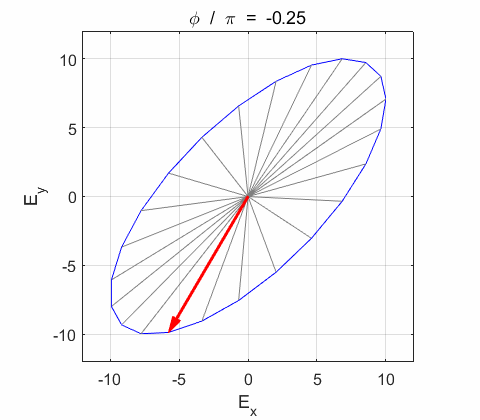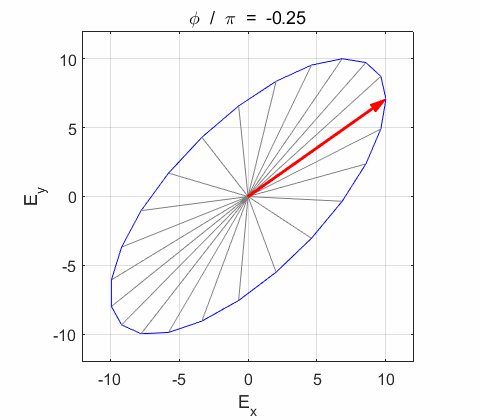
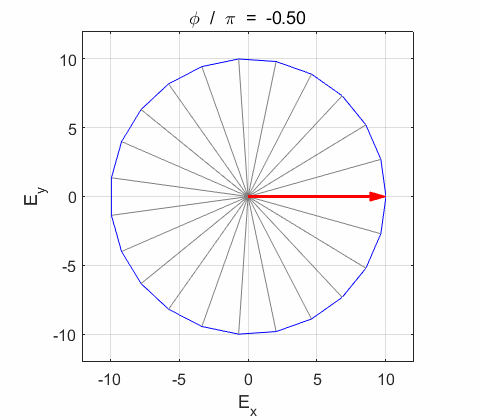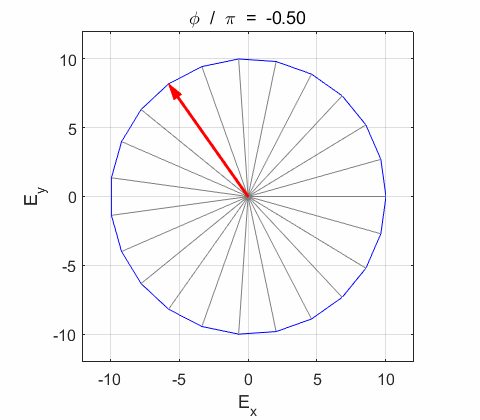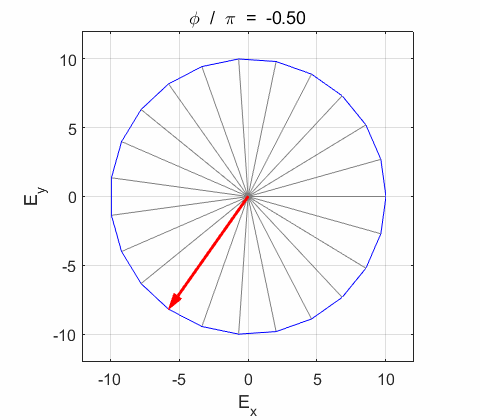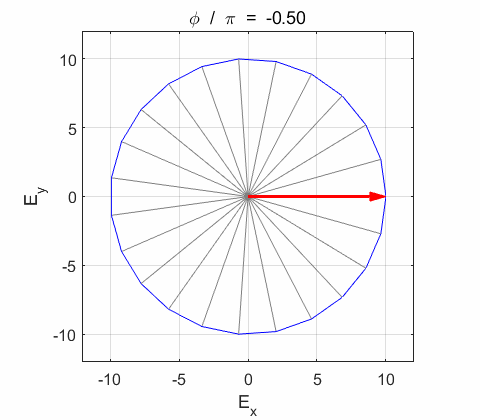
Right-circularly polarized light. When you view the animation, you see the wave approaching you and the rotation of the resultant electric field vector is clockwise: right-circularly polarized light. The convention we are using states that the wave is right-elliptically polarized. Warning: there are other conventions, so you need to know the rule that you are using in stating whether the wave is right or left polarized. Phase difference The
resultant wave is elliptically polarized with the rotation of
the electric field vector
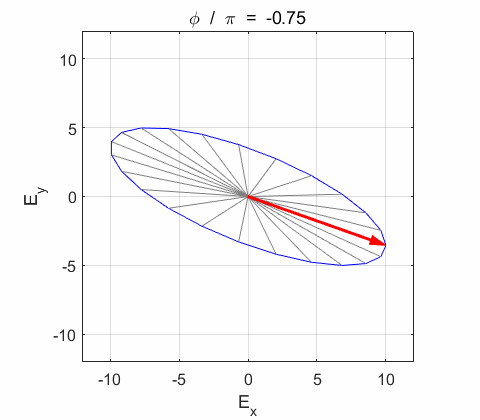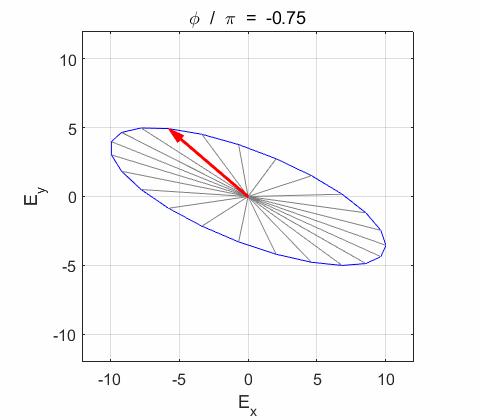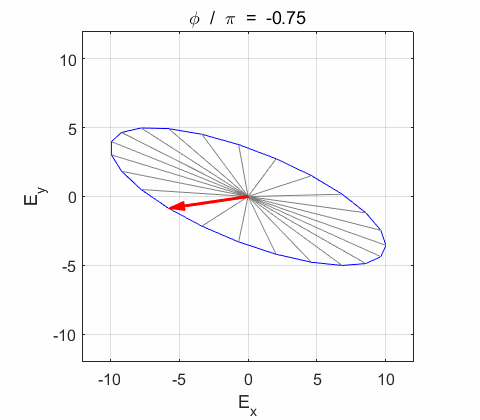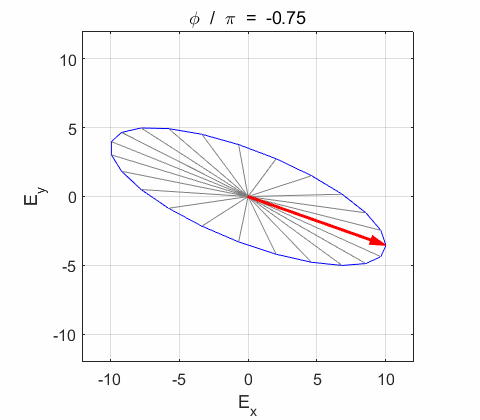
Phase difference The
resultant wave is elliptically polarized with the rotation of
the electric field vector
Phase difference The
resultant wave is elliptically polarized with the rotation of
the electric field vector
Phase difference
The
resultant wave is circularly polarized with the rotation of
the electric field vector Phase difference
The
resultant wave is circularly polarized with the rotation of
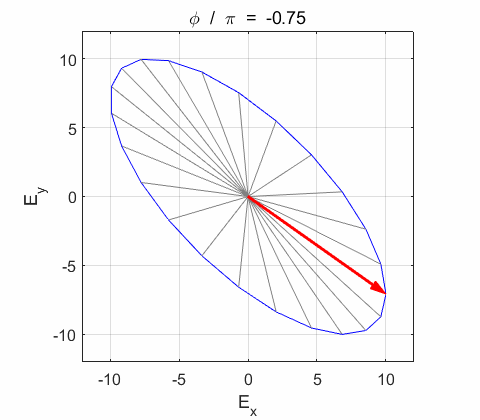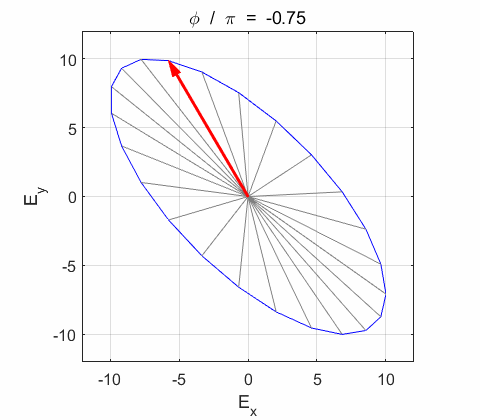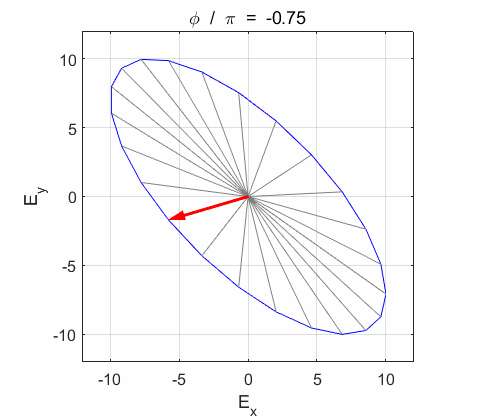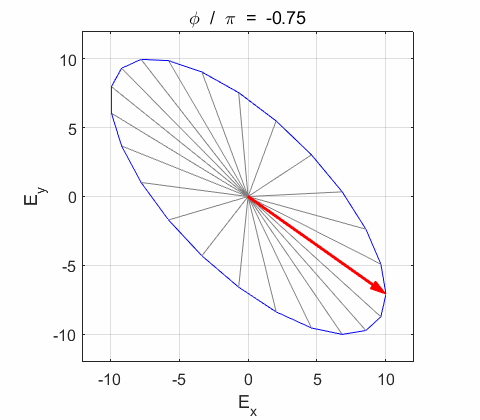
the electric field vector Lissajous figures as a function of relative
phase for orthogonal vibrations The
following animations give a series of Lissajous
figures of relative phase from left elliptical polarization (anticlockwise or counter-clockwise rotation) right elliptical polarization (clockwise rotation)
As far as the mathematical description is concerned, both linear and circular light may be considered as special cases of elliptically polarized light (or more simply, elliptical light). Matlab script
cemPol1.m It is very easy to model the polarization of light using the Matlab complex number functions. Input parameters and calculations
John A Sims email: john.sims@ufabc.edu.br Universidade Federal do ABC, Brazil Ian Cooper email: matlabvisualphysics@gmail.com |