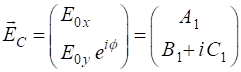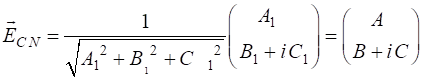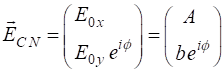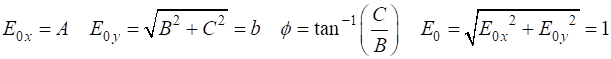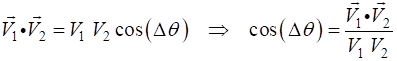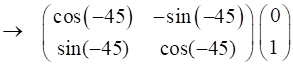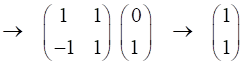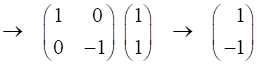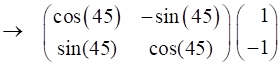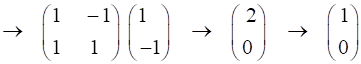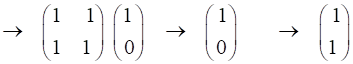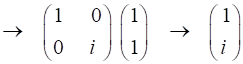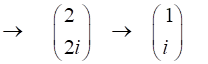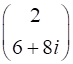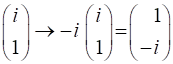Matlab Physics

NUMERICAL ANALYSIS OF OPTICAL AND ELECTROMAGNETIC PHENOMENA

MATLAB EXERCISES: POLARIZED LIGHT

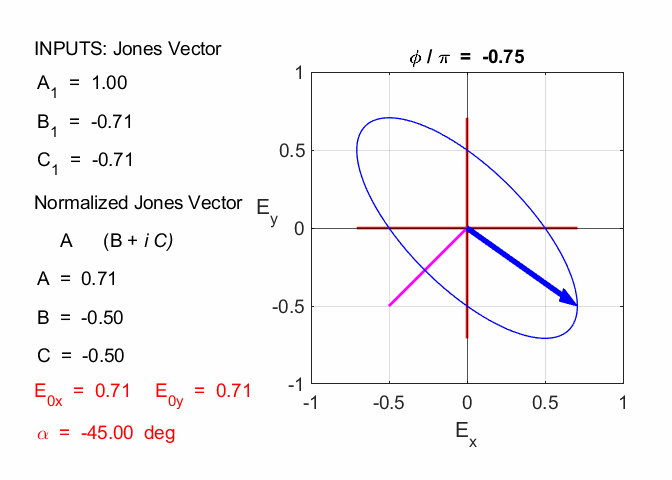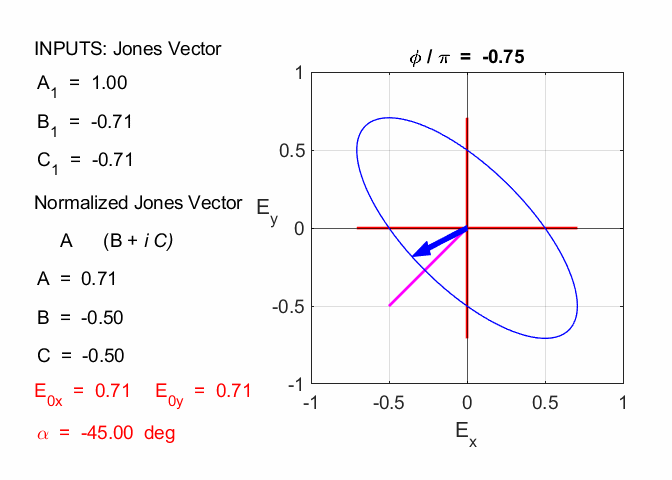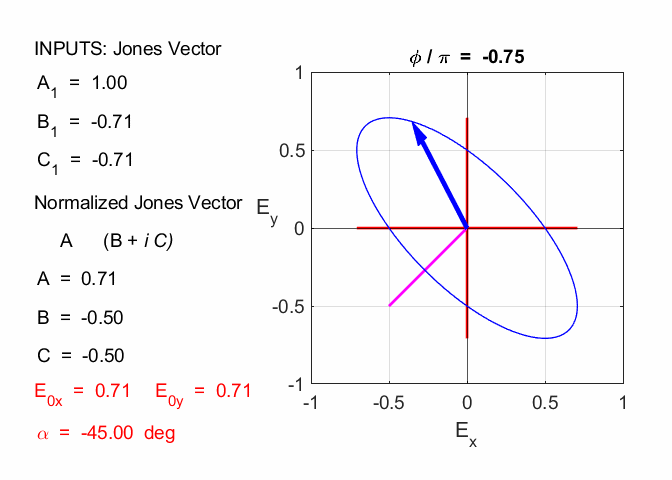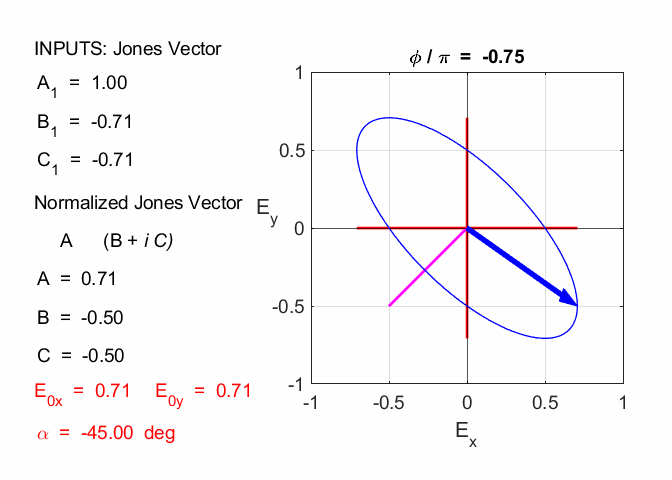
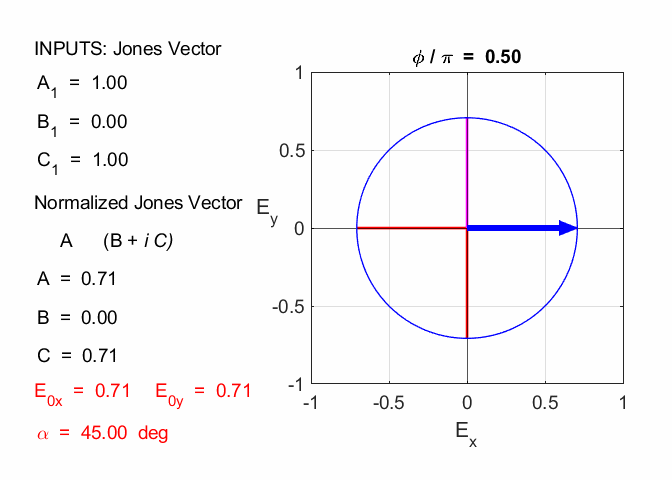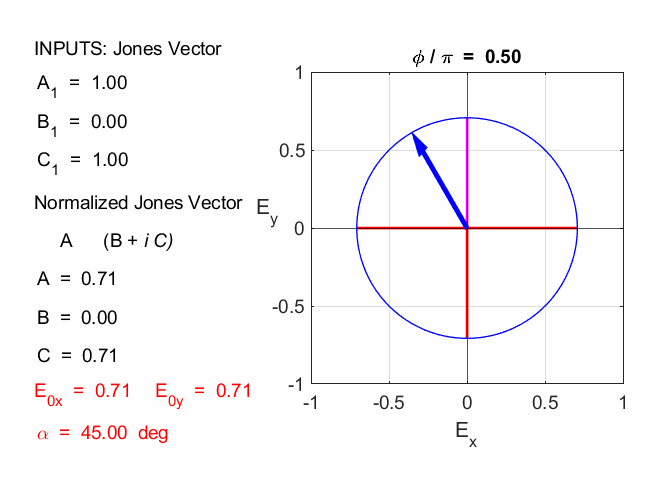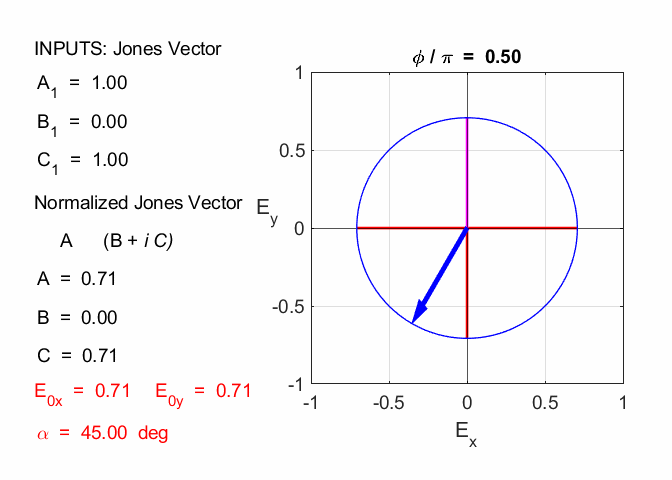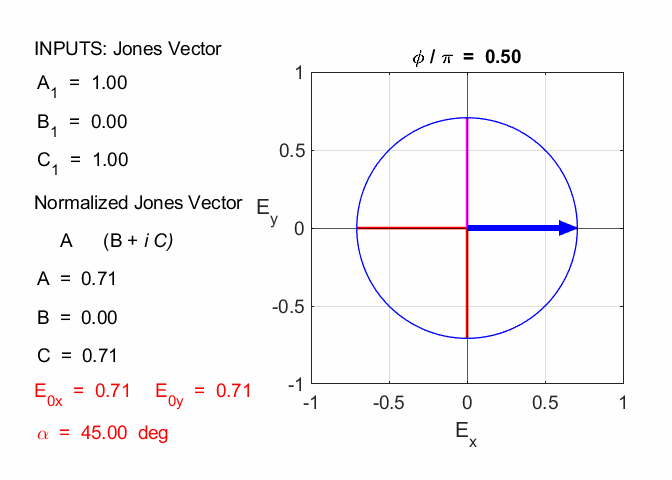
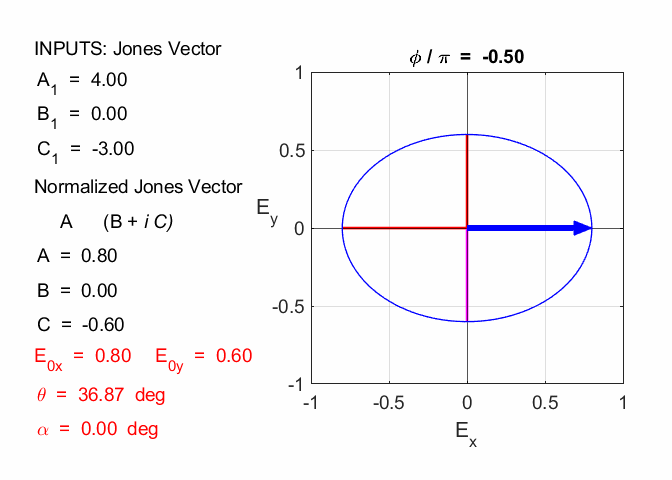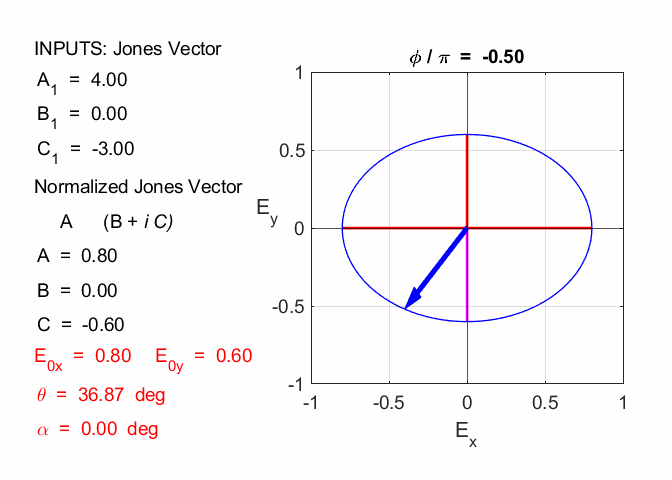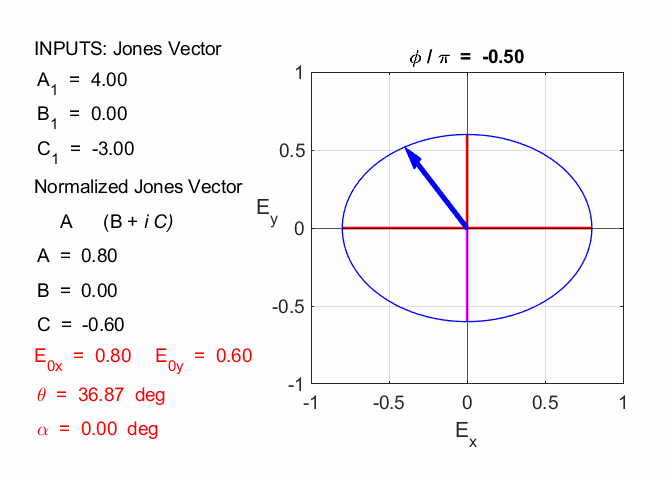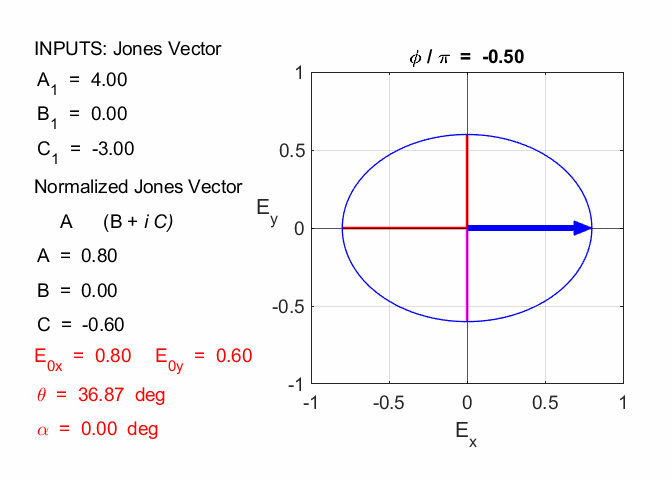
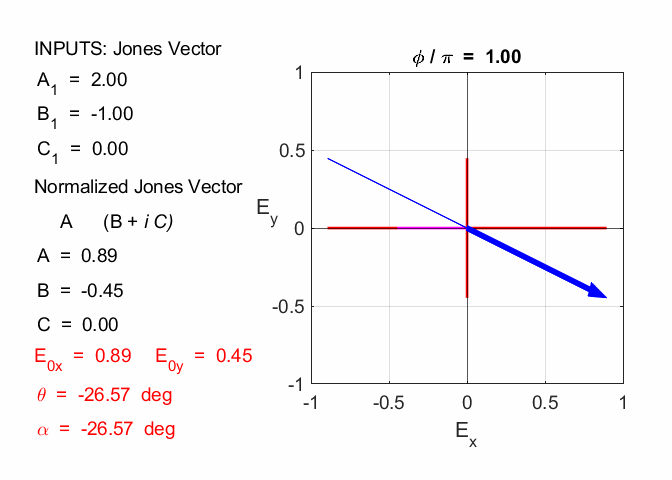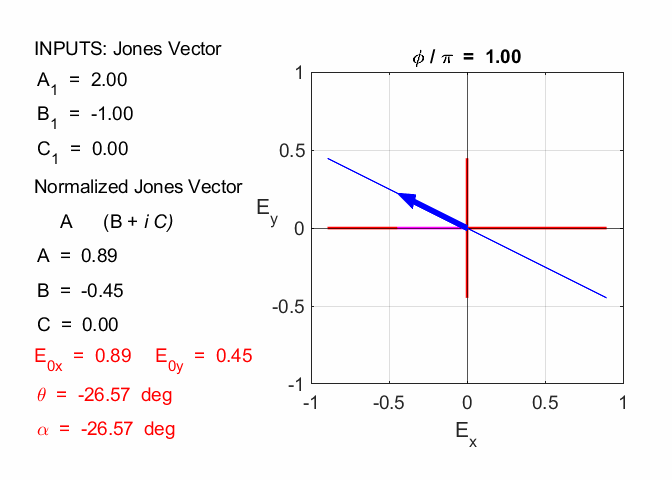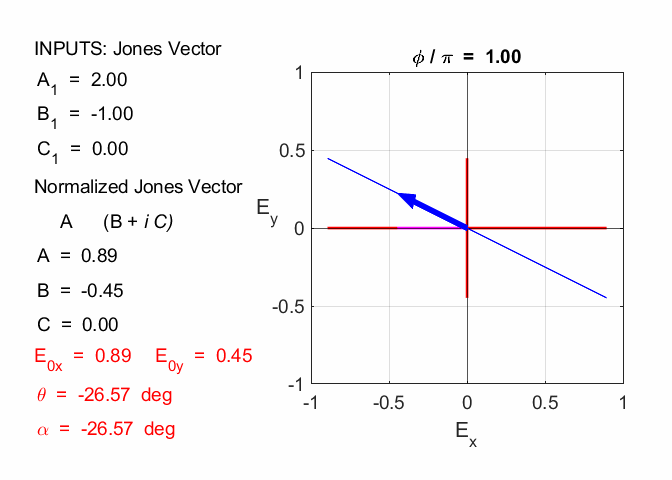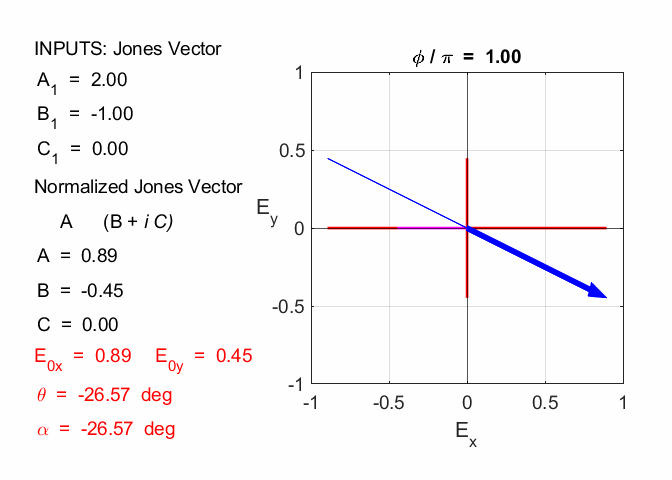
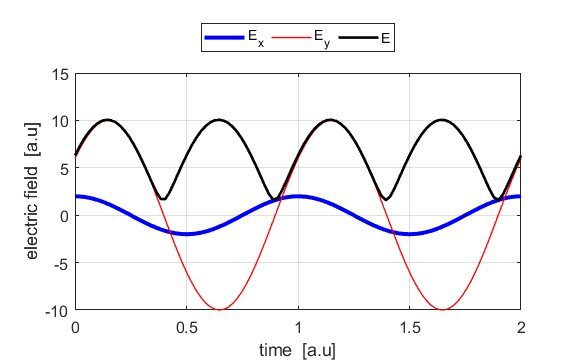
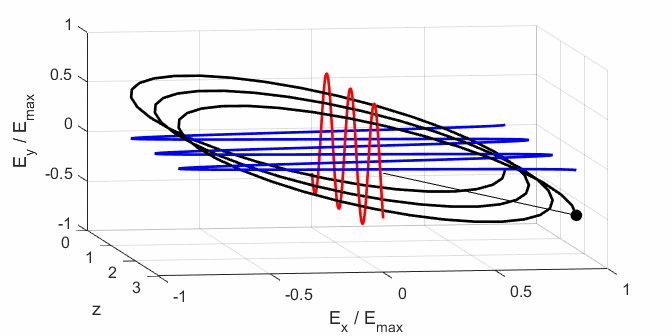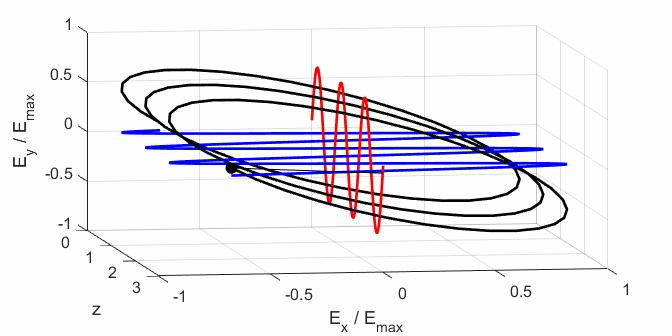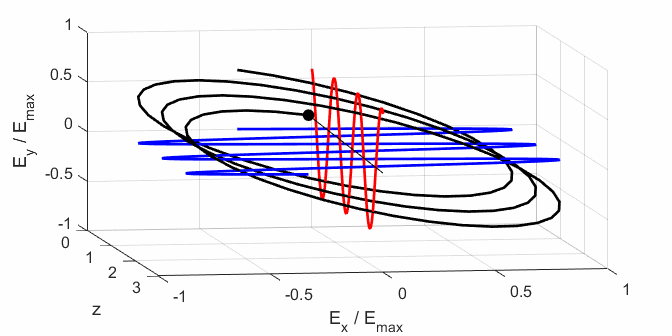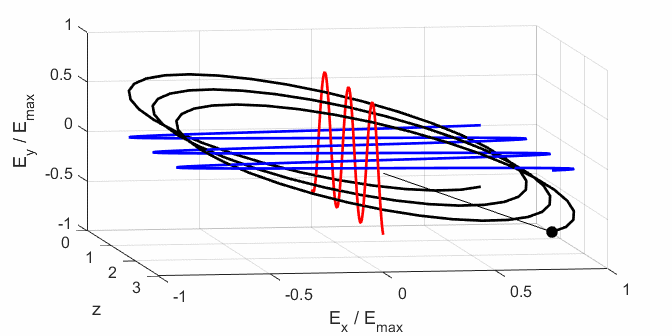
Ian Cooper

matlabvisulaphysics@gmail.com

op_003.m

Animation to show the polarization of light in an XY plane for a light wave propagating in the +Z direction (direction out of the screen, so that you are looking back at the source). The Jones vector parameters A₁, B₁ and C₁ are entered in the INPUT section of the Script. In the CALCULATION section of the Script, the normalized Jones parameters A, B, and C for the Jones vector and the X and Y components of the electric field are calculated. The state of polarization of light is characterised by an elliptical orbit as shown in an animated graphical plot. The animation can be saved as an animated gif file by setting the variable flagS = 1. The Script calls the function arrow.m to draw the electric field vector.

op_005.m

Animation of electric field vector in space and time.

op_004.m

Animation of polarized light incident upon optical elements, and the emergent polarized light. The incident polarized light is specified by its Jones Vector and optical elements by their Jones Matrices. The emergent polarized light is given by its normalized Jones Vector.

Many of the exercise are based on problems from Introduction to Optics, F.L. Pedrotti and L.S. Pedrotti.

Exercise 1

What are the normalized Jones Vectors for each of the following EM waves and give their mode of polarization of each.

1.1

1.2

1.3

1.4

Solution 1

We need to make use of the following

The normalized Jones vector is defined as

where

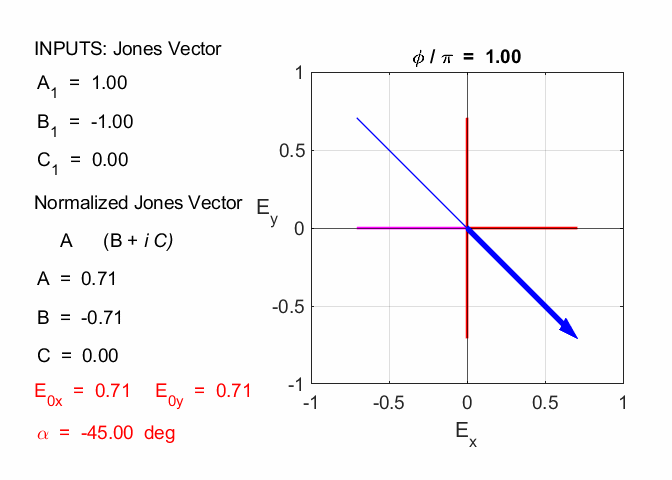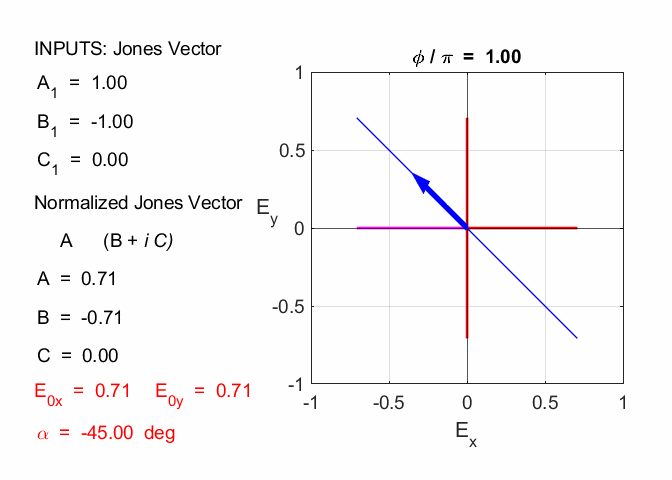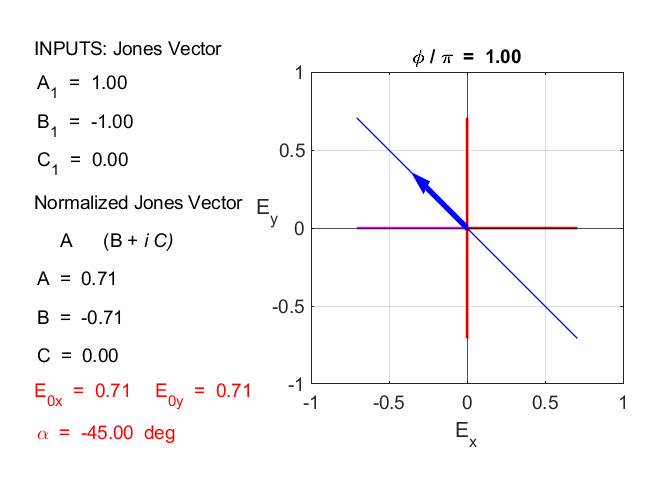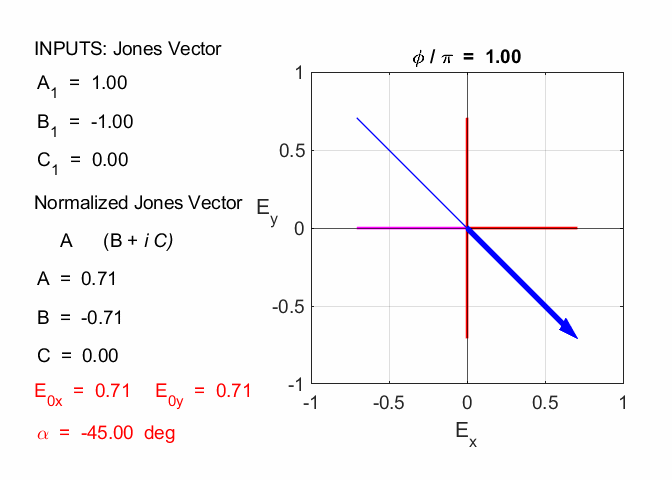
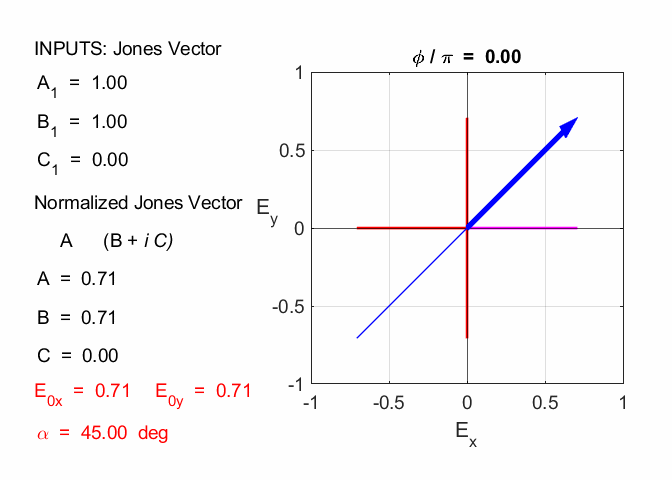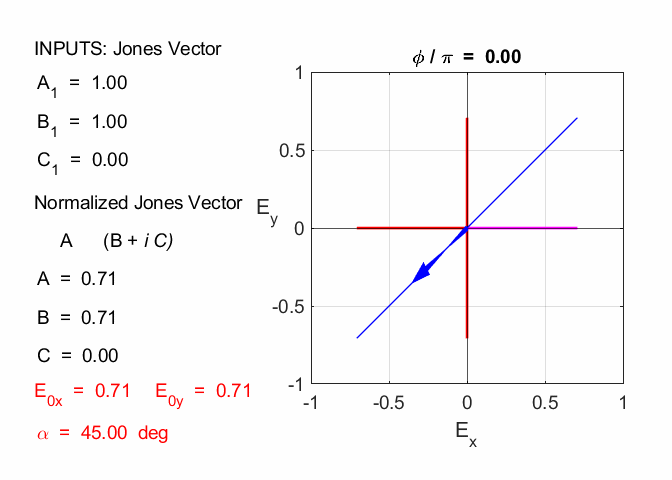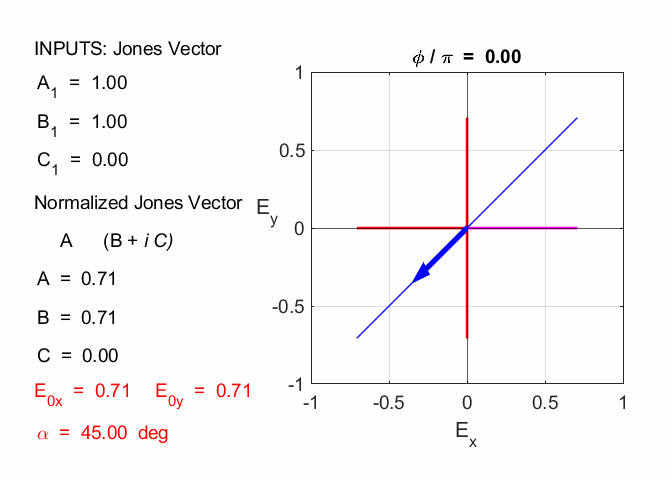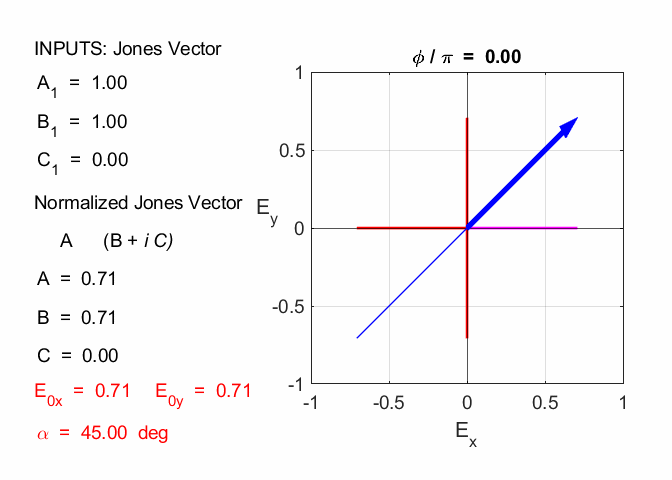
Given and you can use the Matlab Live Editor opLE005.mlx to calculate the Jones Vectors and the Script op_003.m or op_005.m to view the state of the polarization.

1.1 linearly polarized at -45^o

% INPUTS

E0x = 1;

E0y = -1;

phi = 0;

% OUPUTS

A1 = E0x

B1 = E0y * cos(phi)

C1 = E0y * sin(phi)

N = sqrt(A1^2 + B1^2 + C1^2)

A = A1/N

B = B1/N

C = C1/N

      A1 = 1

B1 = -1

C1 = 0

N = 1.4142

A = 0.7071

B = -0.7071

C = 0

1.2 linearly polarized at +45^o

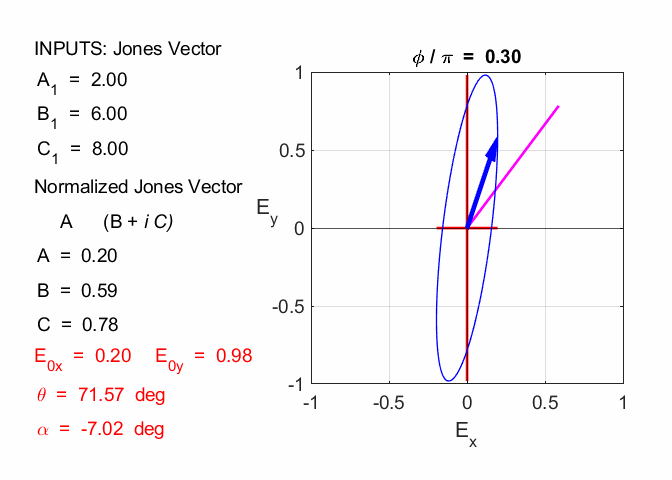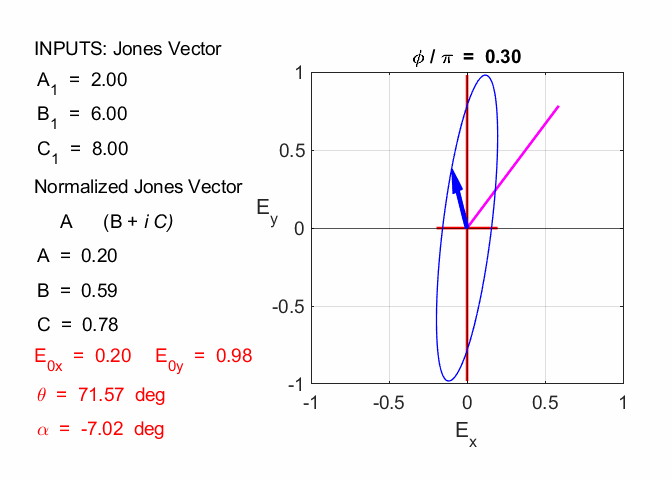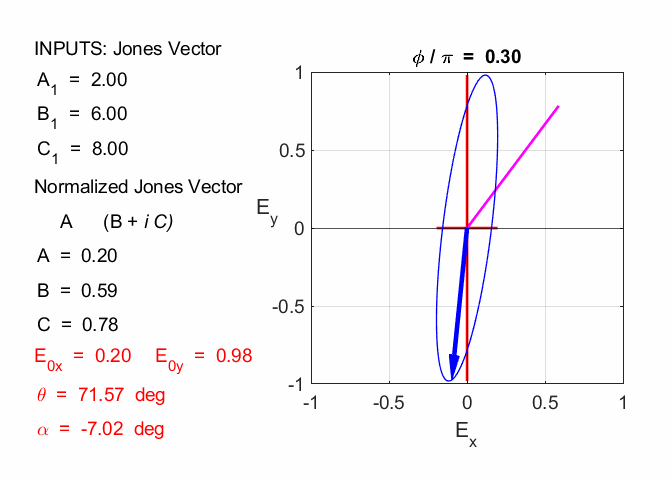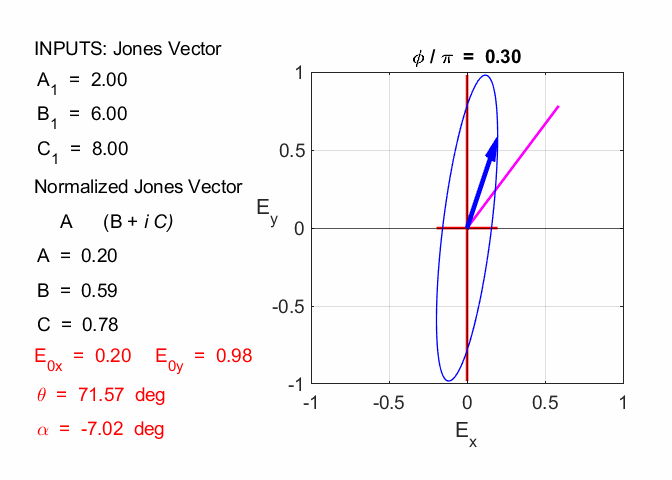
1.3 right elliptical polarization

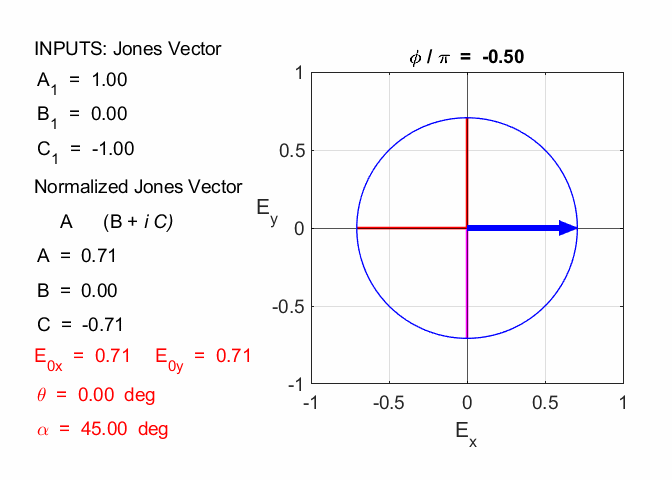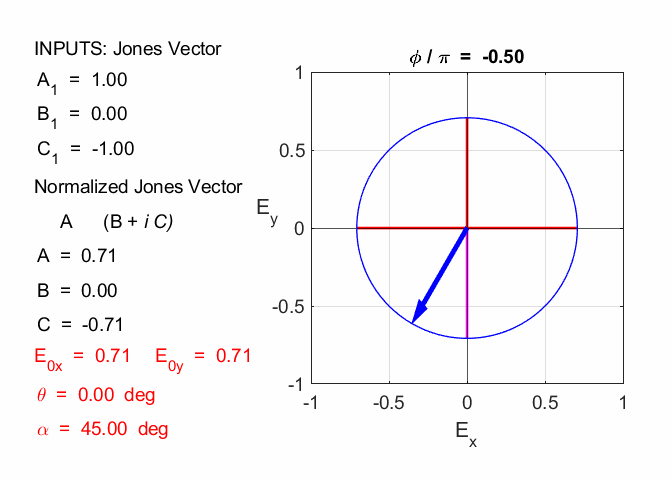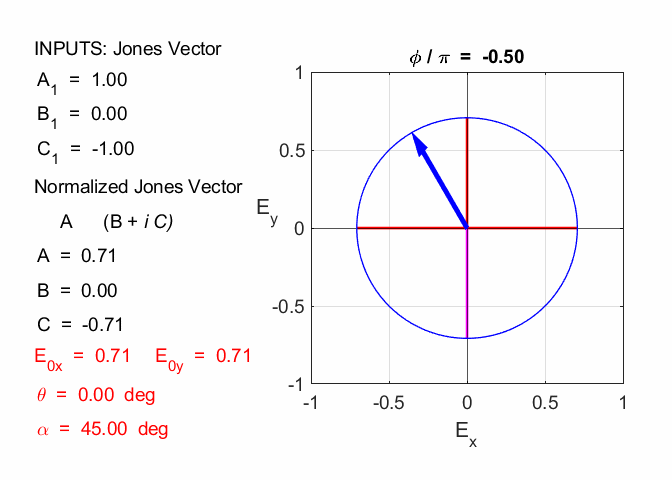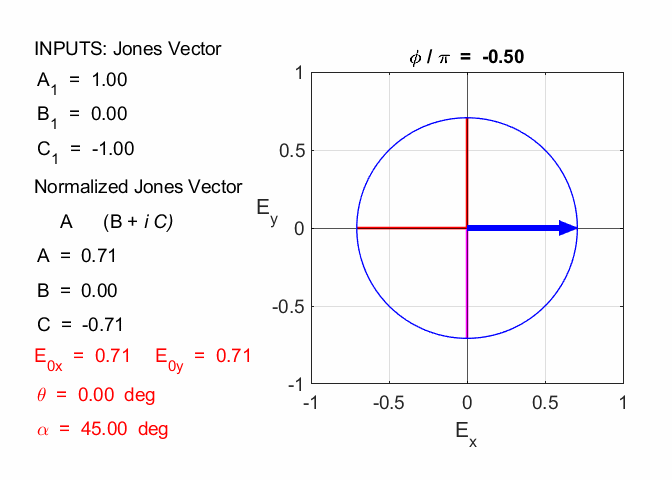
1.4 left circularly polarized

Exercise 2

For each EM wave give its amplitude, propagation direction and mode of polarization.

2.1

2.2

2.3

Solutions 2

You Scripts opLE005.mlx and op_003.m or op_005.m

2.1

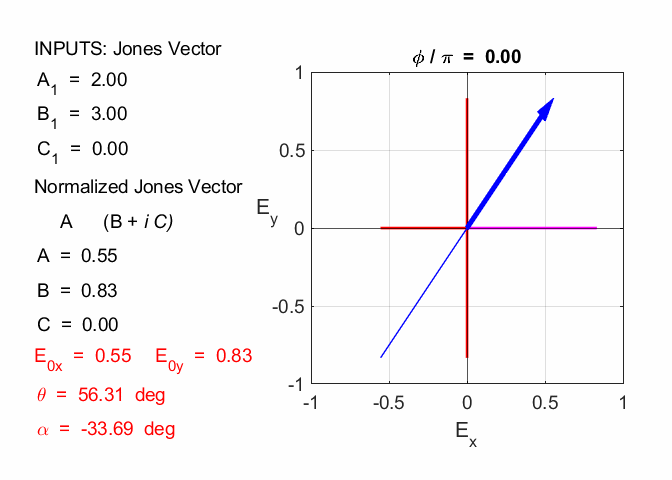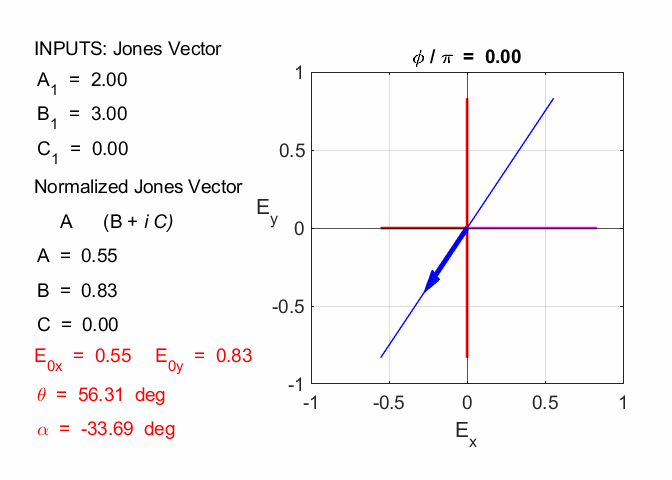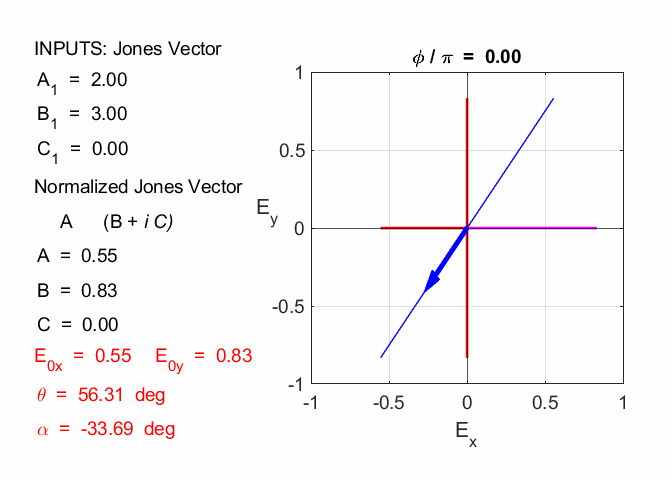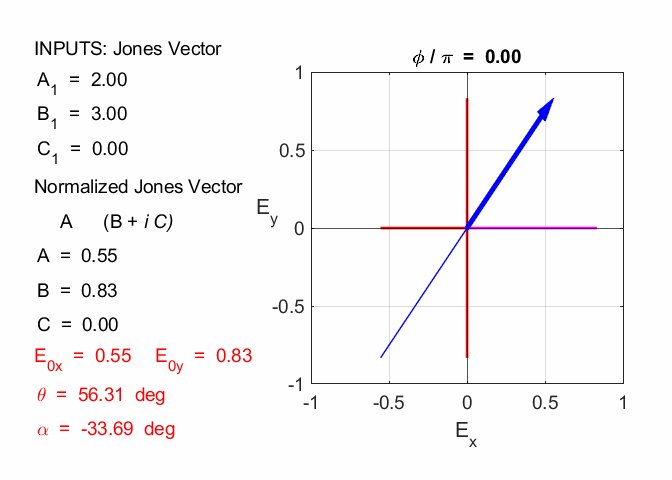
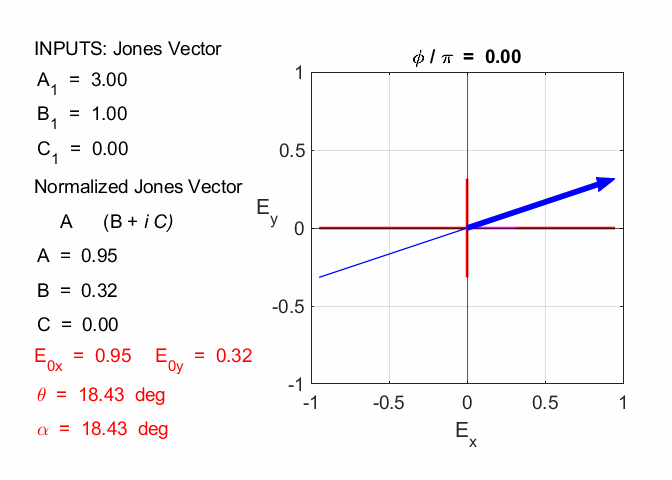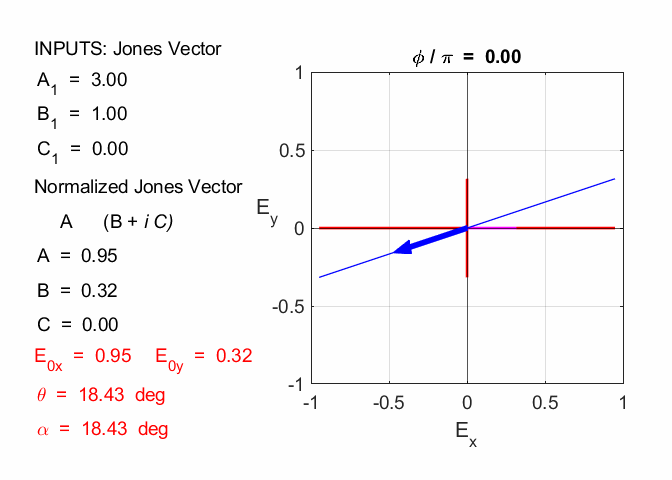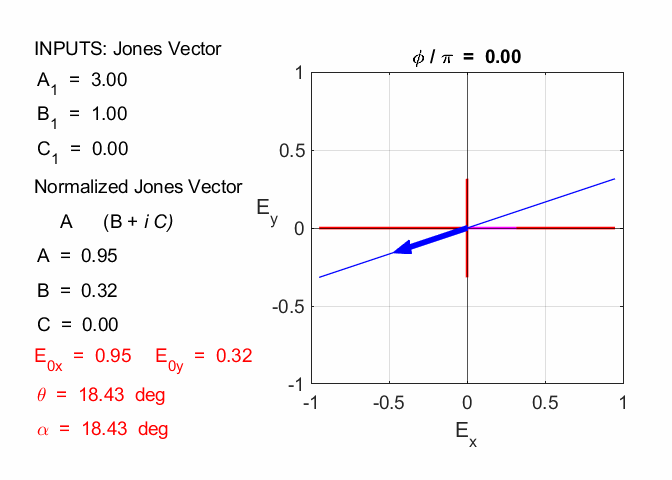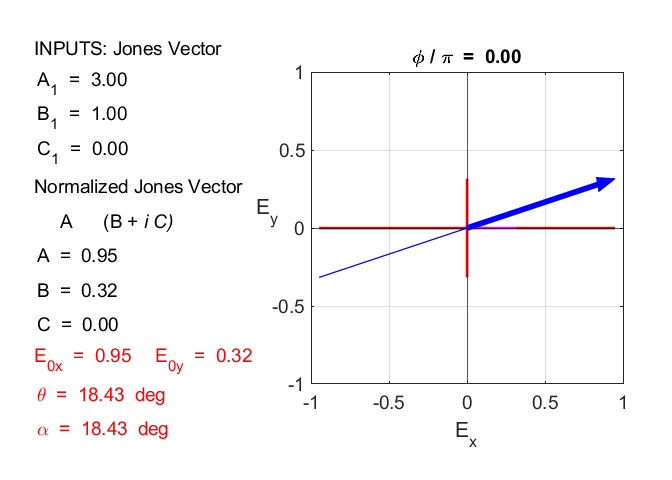
Amplitude = 3.00 travelling in +Z direction linearly polarized in X-direction

2.2

Amplitude = 3.61 travelling in +Z direction linearly polarized at 56.3^o in X-direction

2.3

Amplitude = 5.00 travelling in +Z direction right elliptical polarized

Exercise 3

Two linearly polarized beans are given by

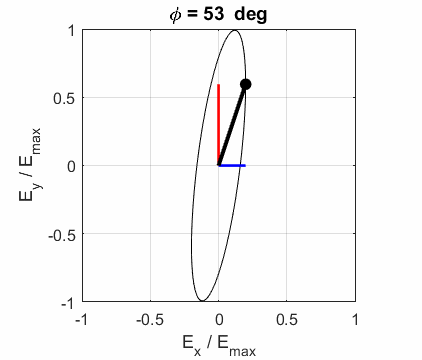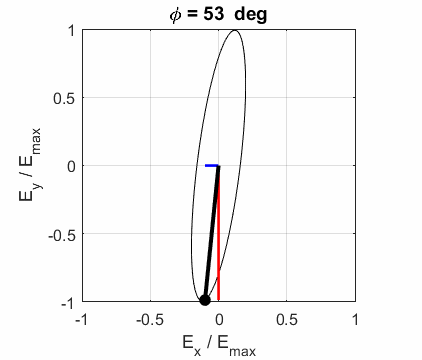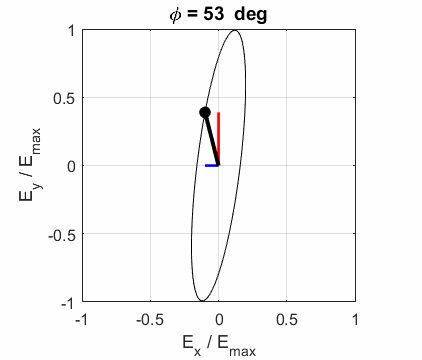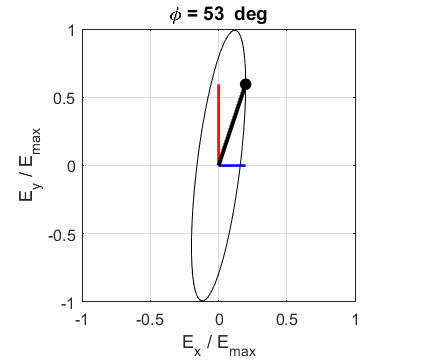
What is the angle between the two planes of polarization?

Solution 3

We can run the Script op_003.m for both waves and determines the angles of inclination of each electric field vector. Note the constants and only affect the amplitudes and do not affect the directions of the plane of polarization, so we can take .

The angle between two vectors can be determined from the dot product of the two vectors

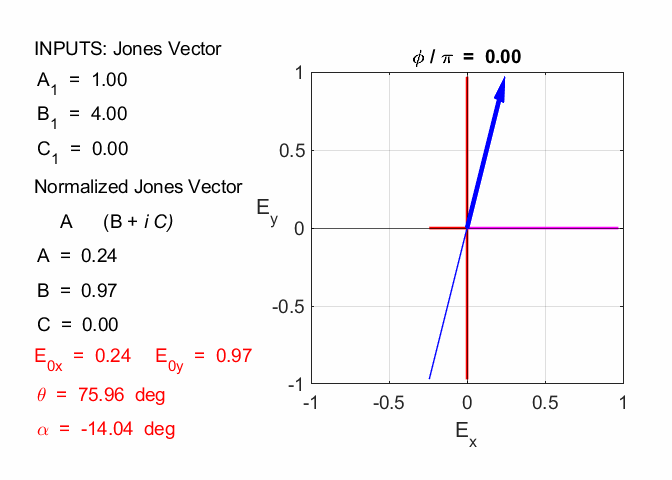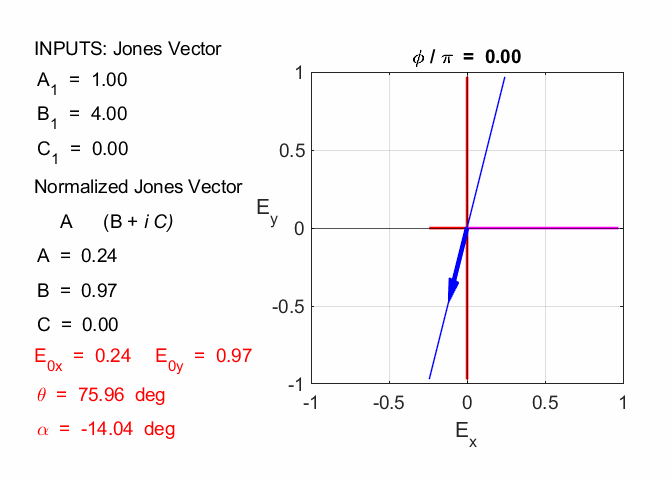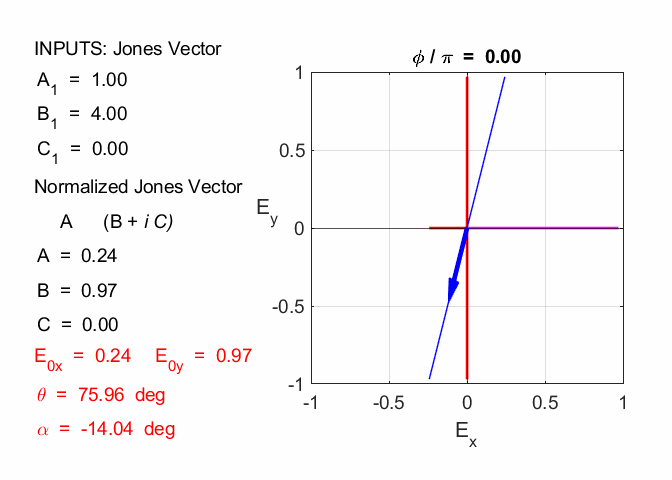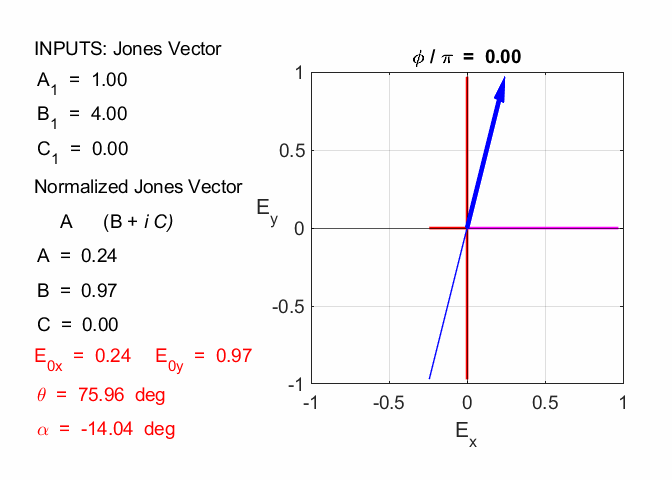
The two vectors for the calculation are the Jones Vector for each EM wave. The calculation can be done using the Live editor Script opLE005.m. The dot product is calculated using the Matlab function dot and the magnitude of a vector is found using the norm function.

E10x = 2;

E10y = -1;

phi1 = 0;

E20x = 1;

E20y = 4;

phi2 = 0;

A1 = E10x

B1 = E10y * cos(phi1)

C1 = E10y * sin(phi1)

V1 = [A1; B1+1i*C1]

A2 = E20x

B2 = E20y * cos(phi2)

C2 = E20y * sin(phi2)

V2 = [A2; B2+1i*C2]

V1dotV2 = dot(V1,V2)

magV1 = norm(V1)

magV2 = norm(V2)

theta = acosd(V1dotV2/(magV1*magV2))

A1 = 2

B1 = -1

C1 = 0

V1 = 2×1

-1

A2 = 1

B2 = 4

C2 = 0

V2 = 2×1

V1dotV2 = -2

magV1 = 2.2361

magV2 = 4.1231

theta = 102.5288

So, the angle between the plane of polarization is 102.5^o.

Exercise 4

A light beam which is linearly polarized vertically is incident upon a series of optical elements: a half-wave plate with its fast axis at 45^o; then a linear polarizer with transmission axis at 45^o; and then a quarter-wave plate with its fast axis horizontal. Find the state of polarization as the light passes through each optical element.

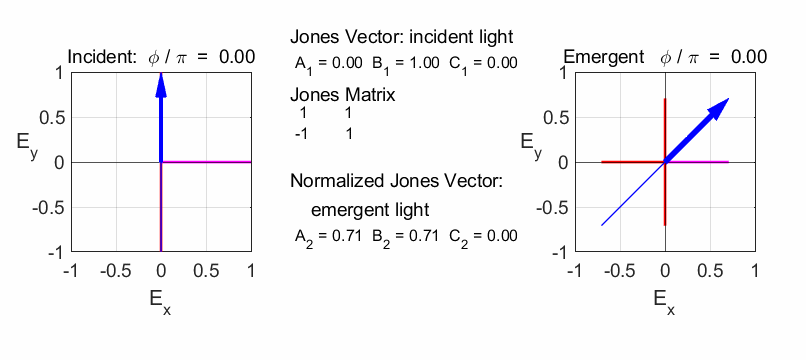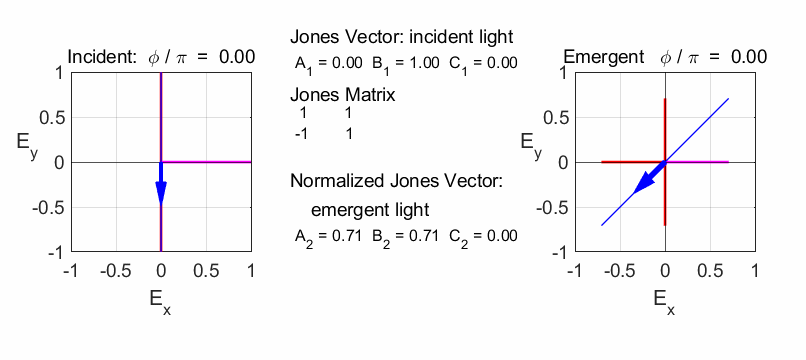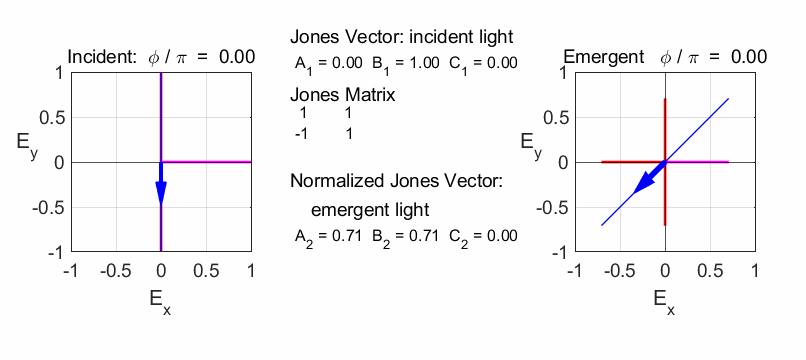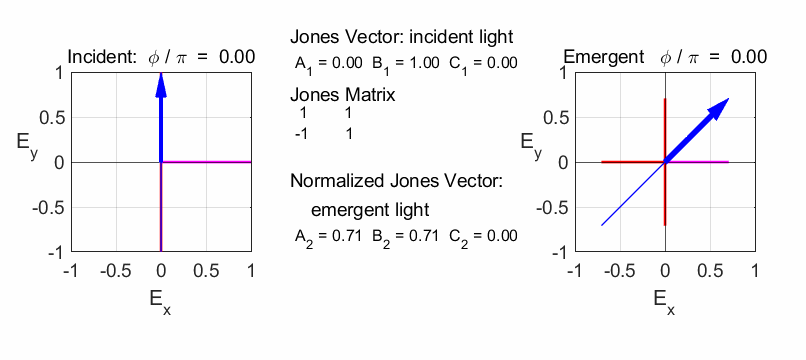
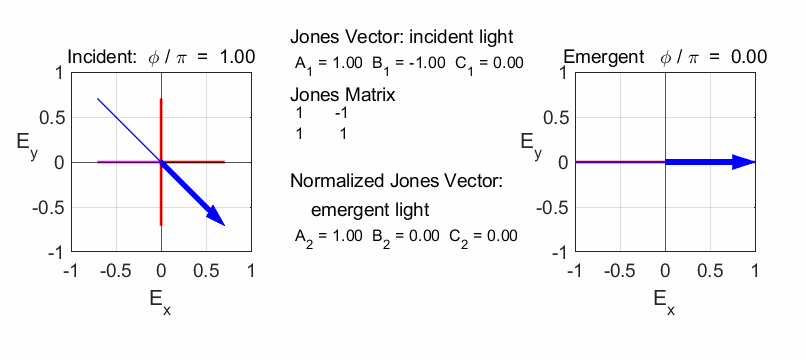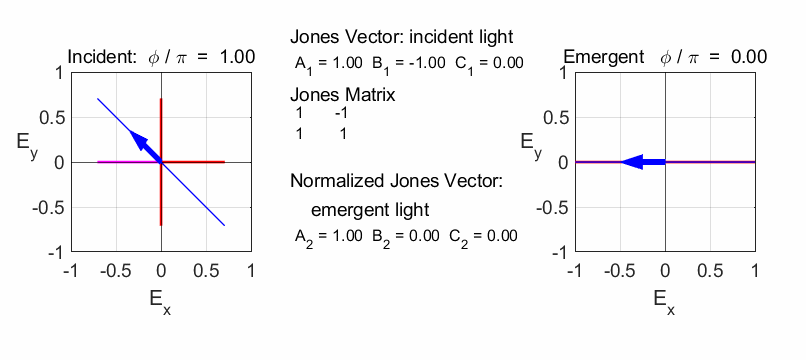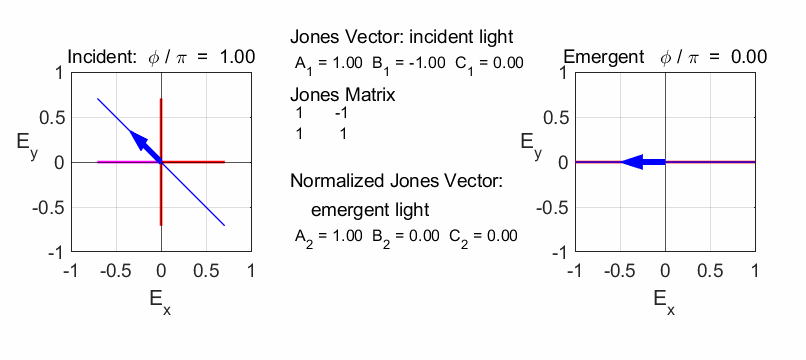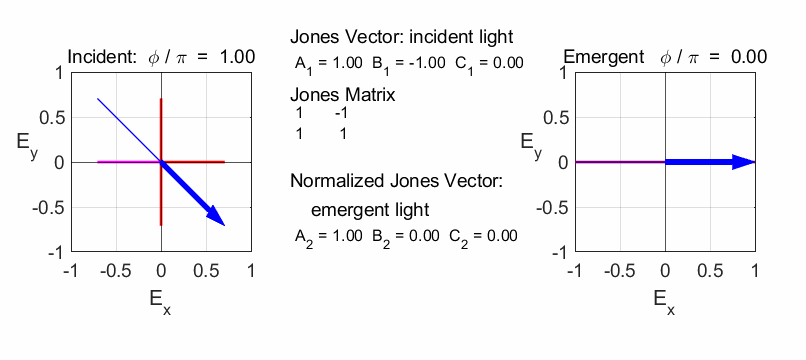
Solution 4 op_004.m

We need to take the fast axis of the half-wave plate to be horizontal. So, we can rotate the half-wave plate by -45^o and the rotate the plane of the incident vertical polarized light also by 45^o. After passing through the half-wave plate, we rotate the plane of polarization through an angle of +45^o. We then consider the linear polarizer with TA at 45^o and then the quarter-wave plate.

Rotation of vertical polarized light by -45^o

linear polarized at 45^o

Half-wave plate (fast axis horizontal)

linear polarized at -45^o

Rotate plane of polarization by +45^o

horizontal linear polarized

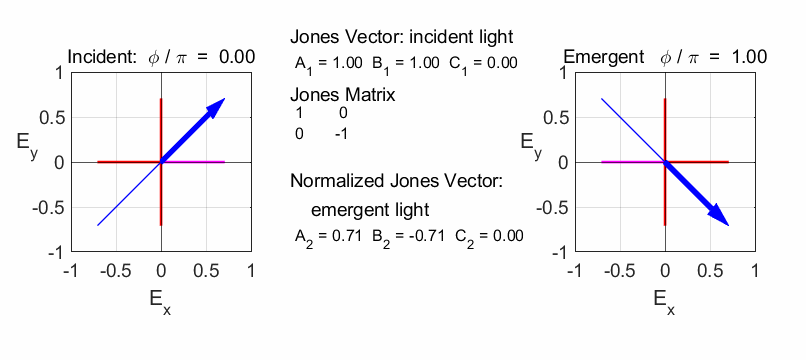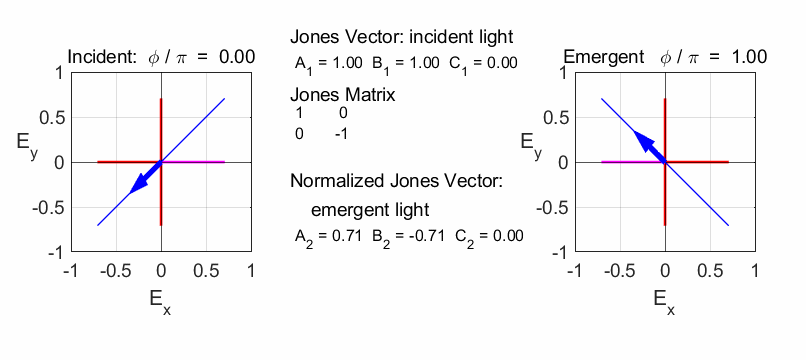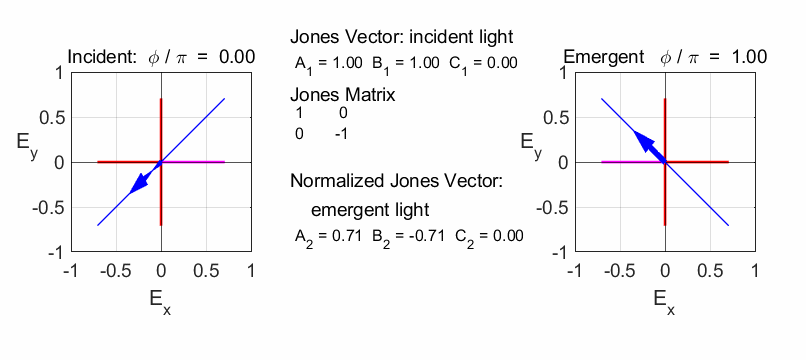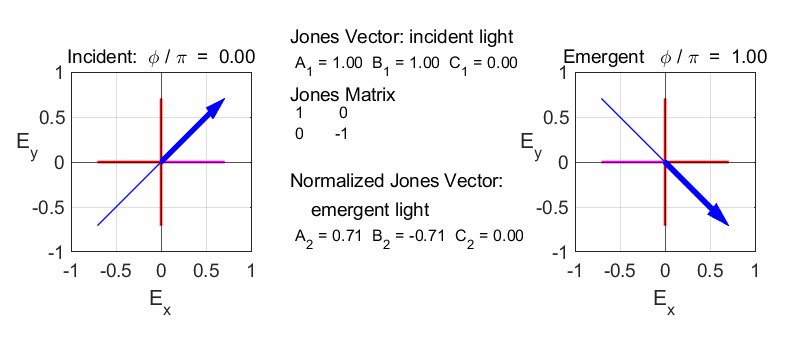
The half-plate oriented at 45^o changes the polarization from vertical to horizontal.

Linear polarizer TA at 45^o

linear polarized at 45^o

Quarter wave plate (fast axis horizontal)

left circular.

We can multiple the Jones Matrices in the Command Window to find the output Jones Vector:

Vin = [1;0]

M1 = [1 1;-1 1] M2 = [1 0;0 -1] M3 = [1 -1;1 1] M4 = [1 1;1 1] M5 = [1 0;0 1i]

Vout = M5*M4*M3*M2*M1*Vin

Vout = 2.0000 + 0.0000i

0.0000 + 2.0000i

Exercise 5

State the polarization mode for each of the following Jones Vectors and the amplitude of the electric field.

(1) (2) (3)

Solution 5 op_003.m op_005.m

(5.1) In our analysis of polarization, we have taken the X component of the electric field to real. Therefore, we can multiply the given Jones Vector by to give . The amplitude of the EM wave is given by the normalization factor its value can be found in the Command Window.