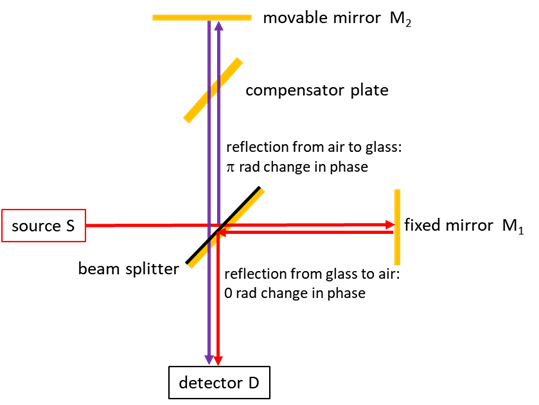
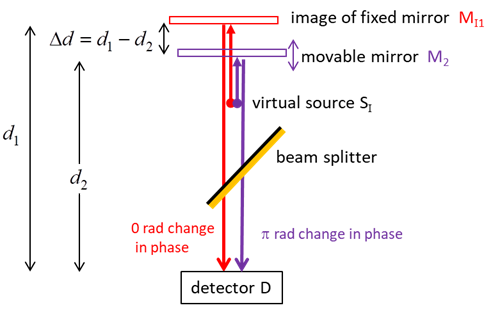
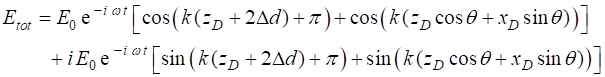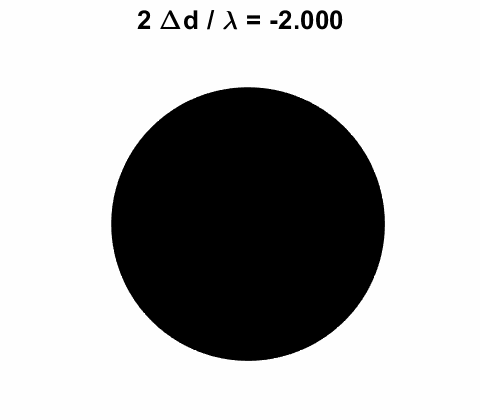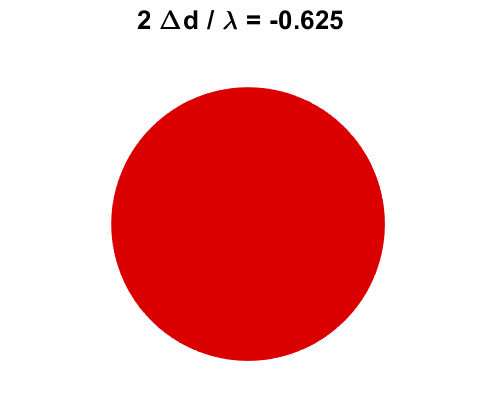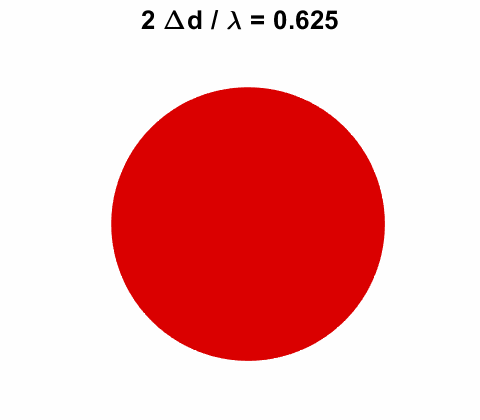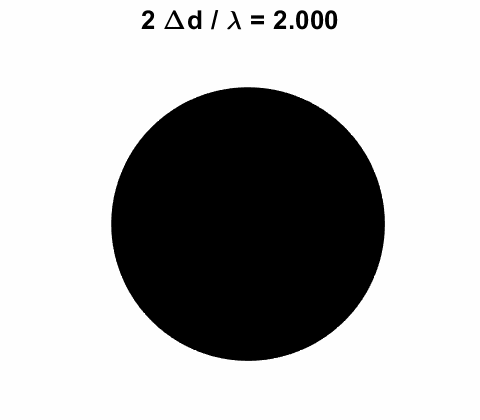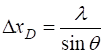|
MICHELSON INTERFEROMETER Fringe Patterns Ian Cooper Email: matlabvisualphysics@gmail.com |
|
MATLAB SCRIPTS opMichA.m Plane wave illumination of Michelson Interferometer. The mirrors are aligned perpendicular to the beam. An animation is displayed of the view on a detector screen as the distance between the mirrors is changes. The Michelson Interferometer can be used to measure small distance and an example of measuring plant growth is used. Calls the function ColorCode.m. opMichB.m Plane wave illumination of Michelson Interferometer with one of the mirrors tilted by a small angle w.r.t. the X axis. A vertical fringe pattern is shown on the detector screen. Calls the function ColorCode.m. opMichC.m Point source illumination of Michelson Interferometer produces circular fringes. Input parameters: wavelength and virtual source separation. Calls the function ColorCode.m. |
|
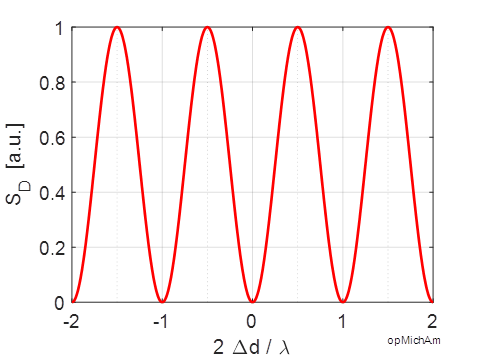
Example Plant Growth The Michelson interferometer can
be used to measure small displacement accurately. For example, it is possible
to measure the growth rate of a plant. The plant was attached to the movable
mirror M2 and its position was adjusted to give a black field of
view on the detector screen. A helium-neon laser was used with a wavelength
0f 632.8 nm. As the plant grew, the distance between the mirrors increased.
So, the fringe pattern changed in a manner as observed in the animation of
figure 5. In an 8.0 hour period, The calculation can be done using the Script opMichA.m %
Plant Growth Calculation %
wavelength [m] wL =
632.8e-9; % Time
interval [h] dt = 8; %
Number of fringes nf = 3420; %
distance moved by plant on mirror 2 [mm] dP = (nf * wL /2) * 1e3; %
rate of growth [mm/h] dPdt = dP/dt; disp('Inputs ') fprintf(' wavelength = %3.1e m
\n',wL); fprintf(' time interval = %3.1f h
\n',dt); fprintf(' fringes = %3.0f \n',nf); disp('Outputs ') fprintf(' growth distance = %3.5f mm \n',dP); fprintf(' rate of growth = %3.5f mm/h \n',dPdt); Inputs wavelength = 6.3e-07 m
time interval = 8.0 h
fringes = 3410 Outputs growth distance = 1.07892 mm rate of growth = 0.13487 mm/h Inputs fringes = 3415 Outputs growth distance = 1.08051 mm rate of growth = 0.13506 mm/h Inputs fringes = 3420 Outputs growth distance = 1.08209 mm rate of growth = 0.13526 mm/h Growth
rate = |
|
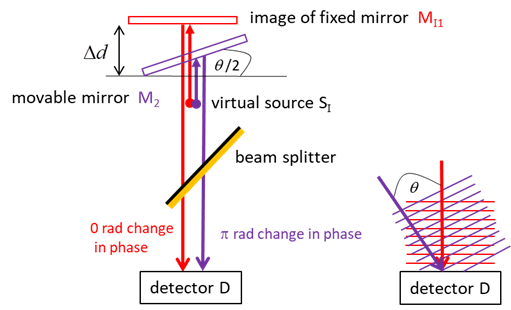
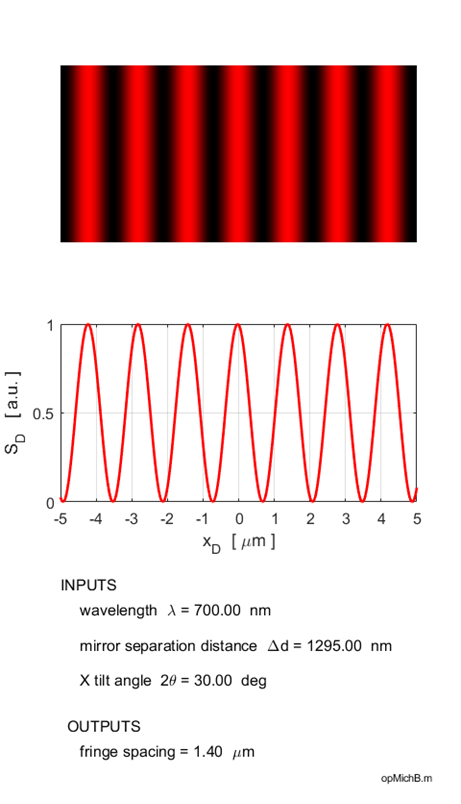
Mirror M2 rotated
about the Y axis Waves reflected by
M2 at an angle The intensity of the detector
screen is due to the interference of the two plane waves. The wavefronts from
the reflection from mirror M1I are parallel
to the screen, while the wavefronts from the reflection from mirror M2
are tilted at an angle to the screen (figure 3). The resultant interference pattern
shows a series of vertical bright and dark equally spaced fringes. The angle The fringes are given by the equation (4) Using equation 4, the spacing
(5) When
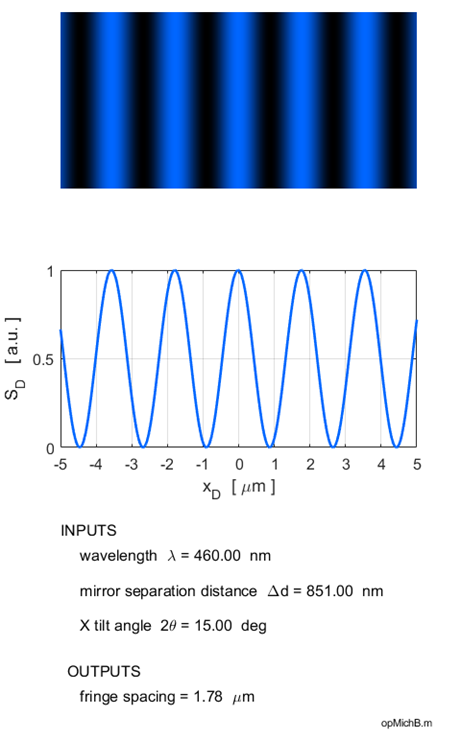
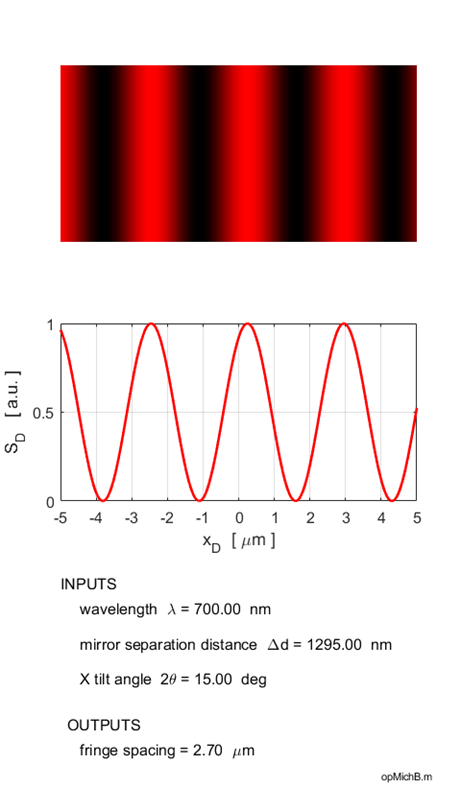
the fringes disappear and the screen becomes uniformly illuminated as described above. The fringe separation becomes smaller as the wavelength decreases and the tilt angle becomes larger. When mirror M2 is moved, then the fringes move in a horizontal direction across the detector screen. The Michelson interferometer is modelled for plane wave illumination with the Script opMichB.m and the Live Editor Script opMichBLE.mlx. Using the Live Editor with the numeric sliders, one can change the wavelength, mirror separation distance and the tilt angle and immediately observe the changes in the interference pattern.
Fig. 6. Fringes of equal thickness are
generated when mirror M2 is tilted. The fringe spacing is reduced as the
wavelength is decreased and the tilt angle is increased as predicted by
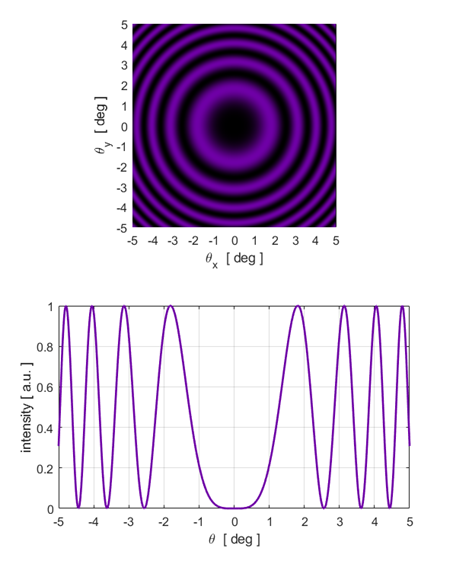
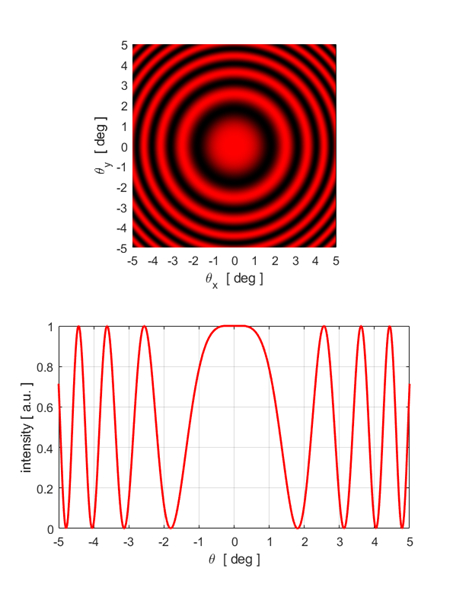
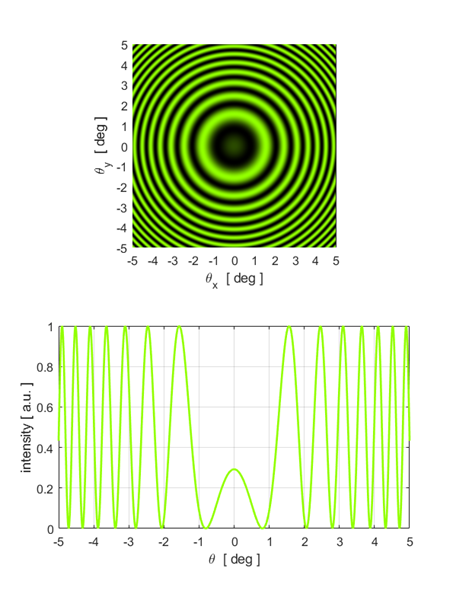
equation 5. Illumination by a monochromatic point source You can calculate the fringe pattern for point source illumination using the script opMichC.m. The input parameters are the wavelength, the distance between the virtual sources and the maximum viewing angle. The spherical waves produce circular fringes on a viewing screen. A dark spot is located at the centre of the fringe pattern if the distance between the virtual source points
A bright spot is located at the centre of the fringe pattern if the distance between the virtual source points
m is called the order of the fringe. Three examples are shown below.
Fig.
7A. Circular fringe pattern:
Fig.
7B. Circular fringe pattern:
Fig. 7C. Circular fringe pattern:
|