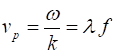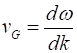|
TRAVELLING WAVE ANIMATIONS PHASE VELOCITY
AND GROUP VELOCITY A plane
harmonic wave propagating along the +Z axis is described by the equation A
amplitude k
wavenumber
The phase velocity vp of the wave is
The group velocity
The superposition of
the two waves gives a resultant complex wave The envelop of the
complex wave moves at the group velocity
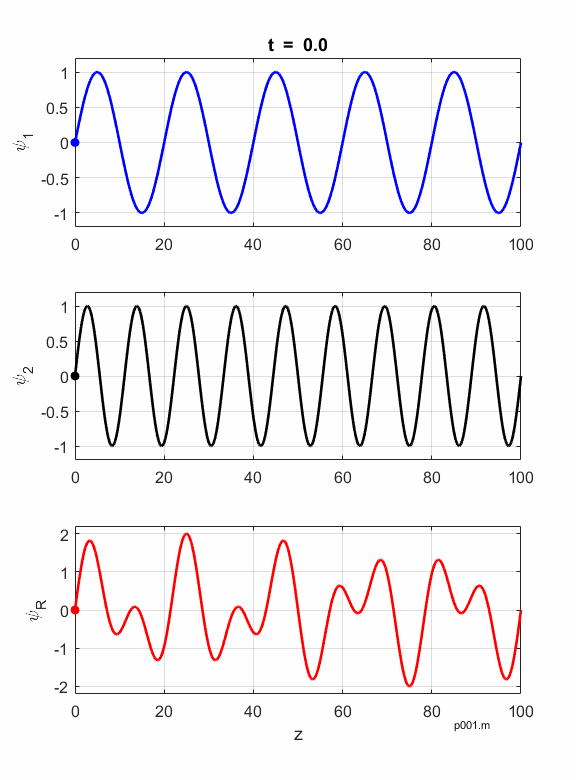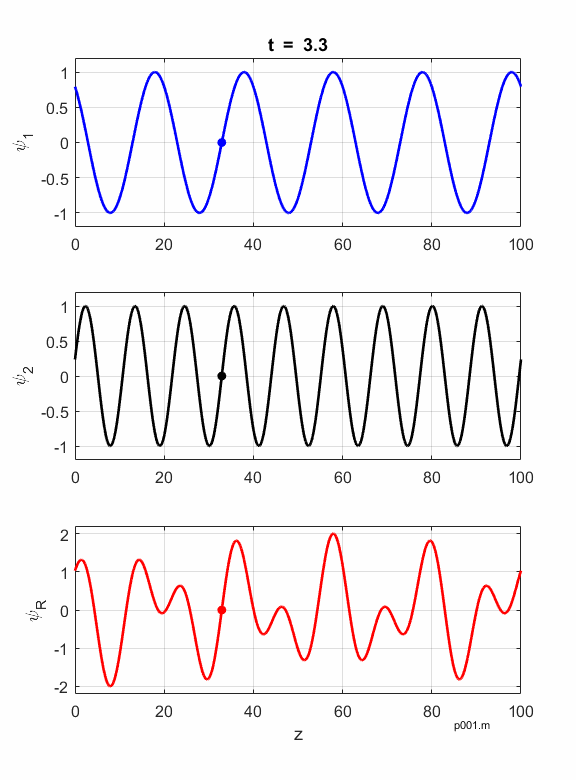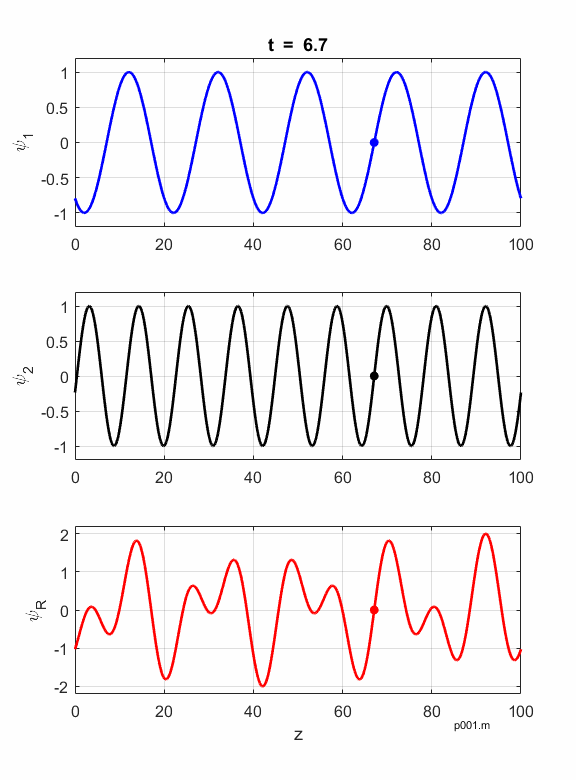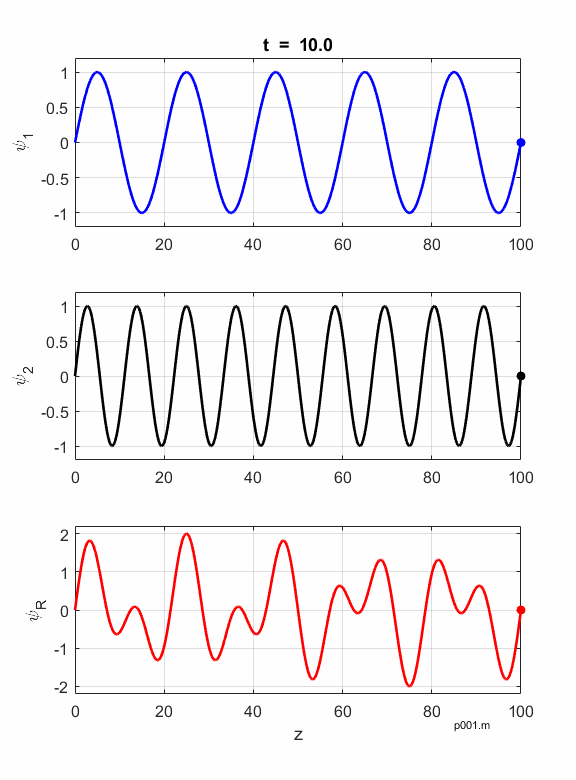
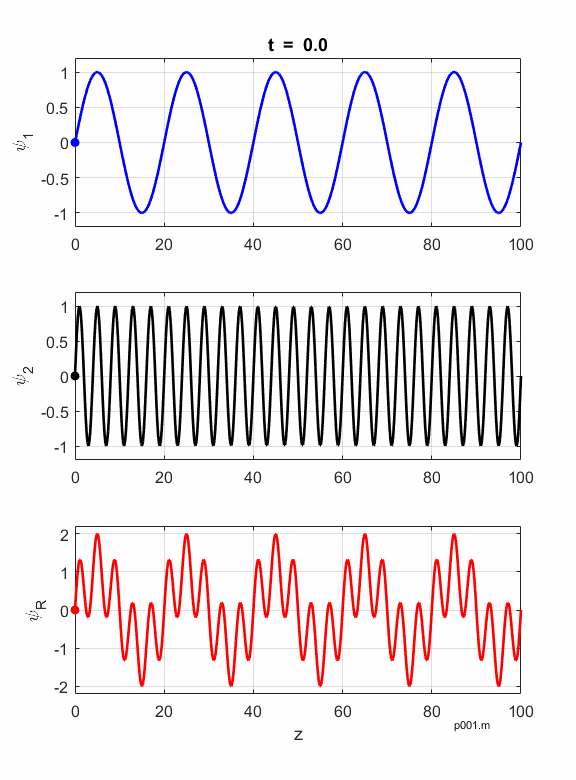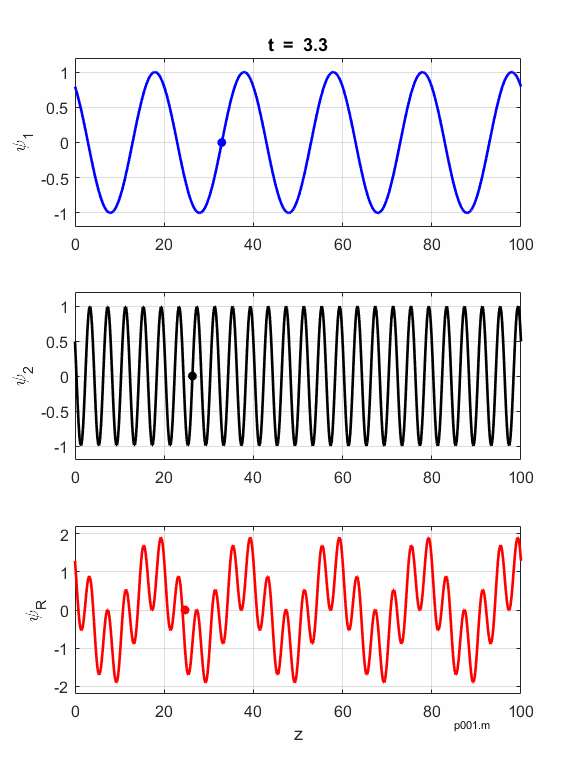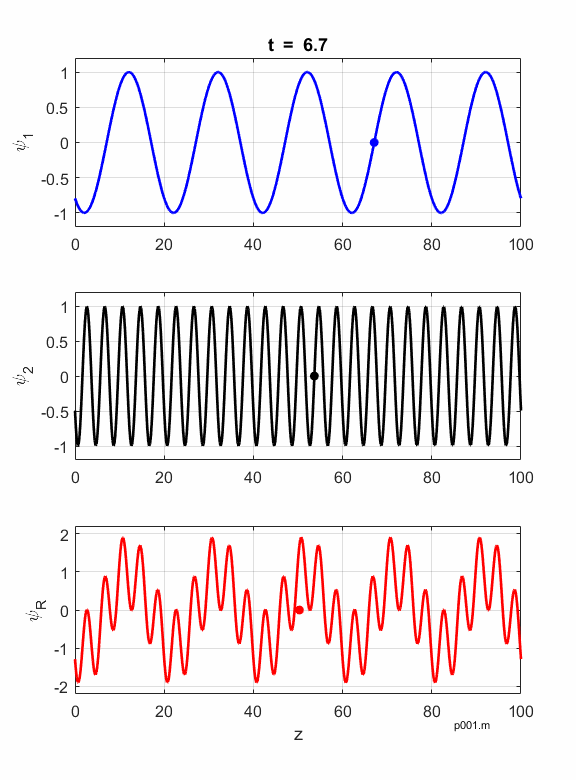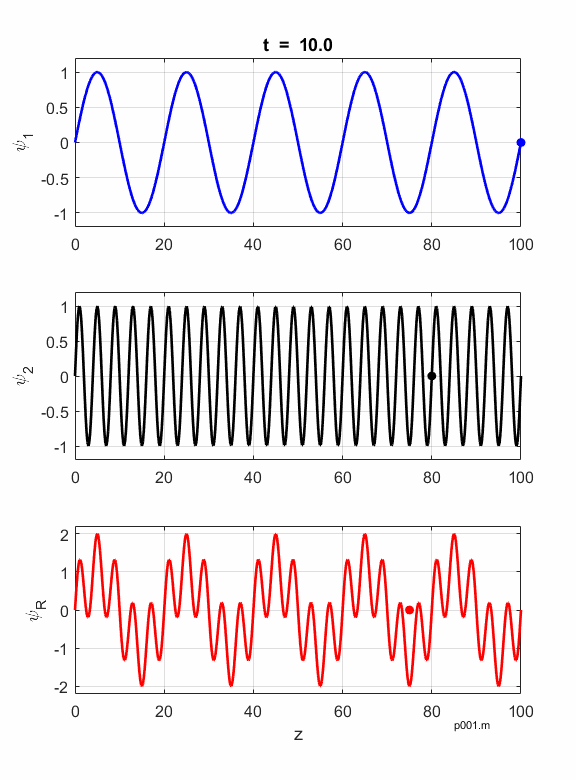
Figures 1 and 2 show
animations of the waves as they travel in a non-dispersive and dispersive
medium. In a non-dispersive medium all frequencies travel with the same phase
velocity and the phase and group velocities are identical. In a dispersive
medium, waves with different frequencies have different phase velocities and
the envelop propagates at the group velocity
Fig. 1. Non-dispersive medium:
Fig. 2. Dispersive
medium: Any comments,
suggestions or corrections please email Ian Cooper Matlab Scripts
Matlab
Script download site p001.m |