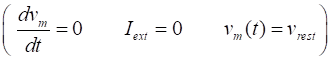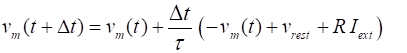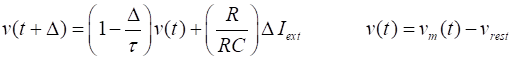|
SPIKING NEURONS LEAKY
INTEGRATE-AND-FIRE MODEL Ian Cooper Any comments,
suggestions or corrections, please email me at
matlabvisualphysics@gmail.com |
|
MATLAB ns_LIF_002.m LIF model of the time evolution of the membrane potential due
to an external stimulus |
|
NEURONS Body fluids are good electrical conductors because salts and
other molecules dissociate into positive and negative ions. The inside of an axon
is filled with an ionic fluid that is separated from the surrounding body
fluid by a thin membrane that is from about 5 nm to 10 nm thick. The
ionic solutes in the extracellular fluid are mainly Na+ and Cl- ions. In the intracellular fluid, the
positive ions are mainly K+ and the negative ions are mainly large
negatively charged organic ions.
Hence, there is a large concentration of Na+ ions outside
the axon and a large concentration of K+ ions inside the axon. The
concentration of the different ion species does not equalize by diffusion
because of the special properties of the cell membrane. In the resting state
when the axon is non-conducting, the axon membrane is highly permeable to K+
ions, slightly permeable to Na+ ions and impermeable to large negative
organic ions. More K+ ions leak out of the cell than Na+
ions that leak into the cell. This leaves the inside of the cell more
negative than the outside. A potential difference therefore exists across the
cell membrane because of the difference in the concentration of ions in the
extracellular and intracellular fluids. This potential difference is called
the membrane
potential vm(t). The outside of the cell is taken as the
reference potential 0 V. The resting membrane potential has a strong negative
polarization and is constant at about -65 mV. This negative membrane
potential restricts the further diffusion of the K+ to the outside
of the cell so that equilibrium is established where the electrical forces
balances the chemical forces. Thus, the membrane acts as a capacitor in
parallel with a resistor. The mechanism for the generation of an electrical signal by a
neuron is conceptually simple. When a neuron receives a sufficient stimulus
from another neuron, the permeability of the cell membrane changes. As a
result of the changes in membrane permeability, the sodium ions first rush
into the cell while the potassium ions flow out of it. The movement of the
ions across the membrane constitutes an electric current signal which
propagates along the axon to its terminations. These membrane currents
depolarize the cell so that the interior of the cell becomes positive and a
neuronal voltage signals is generated. These short voltage pulses are called spikes
or action
potentials and have a duration of less than a few milliseconds and
have a peak about +40 mV. The action potential propagates along an axon
without a change in shape. LEAKY INTEGRATE-AND-FIRE NEURON MODEL We can start the analysis of the
electrical properties of a neuron using the simplest possible model to
generate action potentials, known as the leaky integrate-and-fire (LIF) model. The
membrane of a nerve cell separates the intracellular and extracellular fluids
with inside of the cell more negative than the outside of the cell in its
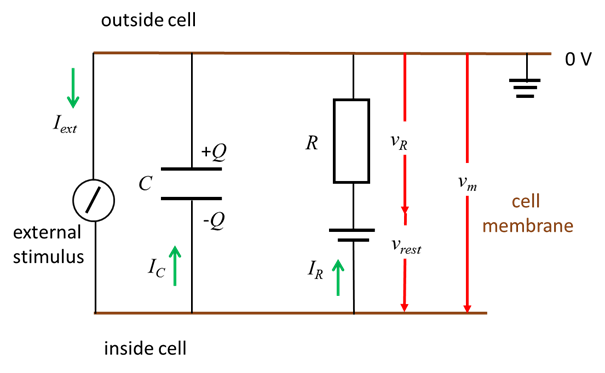
resting state. The electrical properties of the cell membrane are modelled as
a parallel circuit consisting of the membrane capacitance C and the
membrane resistance R in
series with a battery with an emf
equal to resting potential
vrest
and driven by some external stimulus (figure A).
Fig. A. RC circuit
model of the nerve cell membrane used in the LIF
model. Capacitor current
Leakage current through resistor
Kirchhoff’s current law
(1) Equation 1 is the leaky integrate-and-fire (LIF) differential
equation for the membrane potential We can solve equation 1 using the finite
difference method to compute the
membrane potential at a series of time steps of duration
(2)
The spiking events are not explicitly modelled in
the LIF model. Instead, when the membrane potential vm(t) reaches a certain threshold vTH (spiking threshold), it is
instantaneously reset to a lower value vreset (reset potential) and the leaky
integration process described by equation 1 continues with the membrane
potential set at vreset. However, we can
artificially produce a spike when To add just a little bit
of realism to the dynamics of the LIF model, it is
possible to add an absolute refractory period SIMULATIONS The mscript ns_LIF_002.m can be used
to solve equation 2 for different time dependent external stimuli. Typical parameters used in
the modelling are:
The variable flagS is used to select the function for the
external stimulus current input and
flagF for the calculation of the firing rate
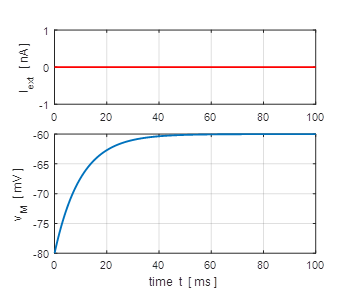
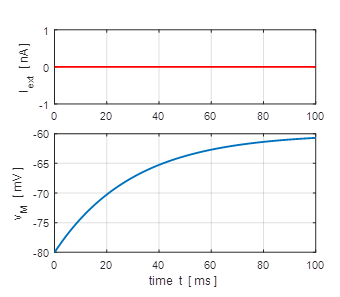
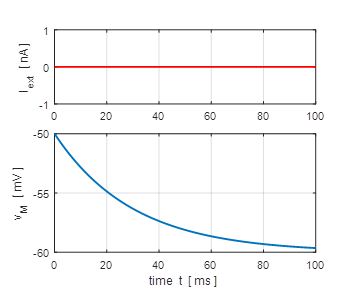
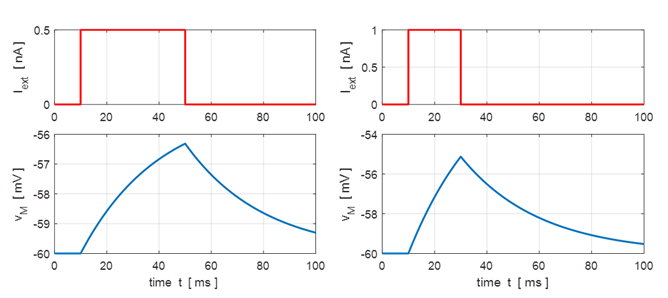
and f – I curve. Simulation 1: Subthreshold regime / Free solutions Exponential decay of membrane potential to resting potential. The larger the
time constant, then the more slowly the membrane potential decreases towards
the resting value for the membrane potential. |
|
Fig.
1A. Depolarization of the
membrane. (flagS = 1) |
Fig.
1B. Depolarization of the
membrane. (flagS
= 1) |
|
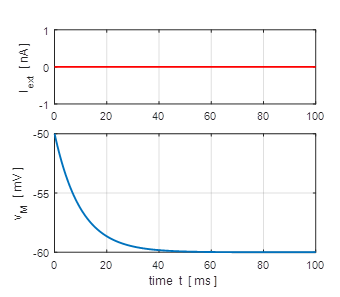
Fig. 1A. Hyperpolarization of the
membrane. (flagS = 1) |
Fig. 1B. Hyperpolarization of the
membrane. (flagS
= 1) |
|
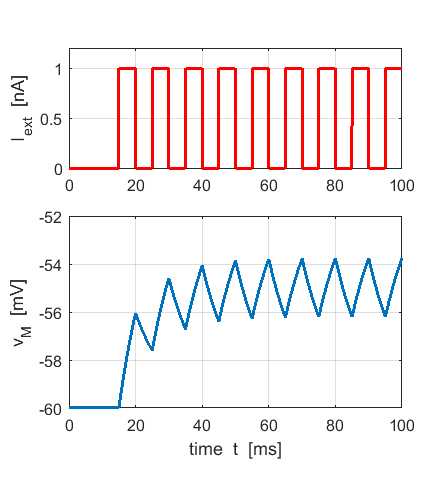
Simulation
2: Subthreshold regime
(pulse input)
Fig. 2. A series of
input pulses results in a linear summation of the membrane response to each
pulse. The membrane potential
remains at a value less than the threshold potential. No spikes are
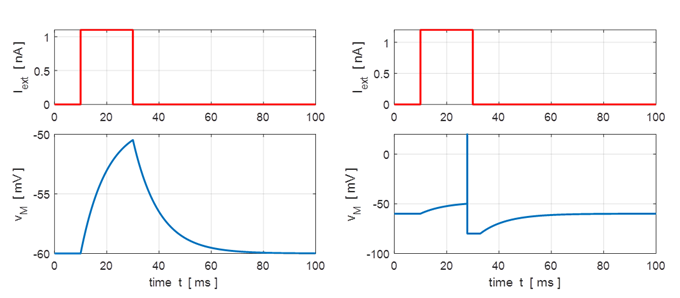
generated. (flagS = 2) Simulation 3: Subthreshold regime (pulse input) When a short pulse acts as
the external stimulus most of the charge Q is deposited onto the capacitor and very little charge
passes through the resistor. Initially the capacitor is charged and then
discharges through the resistor as the input stimulus value goes to zero. Let the width of the input
pulse be
(3)
In the subthreshold
regime, equation 3 implies that for short input pulses which have the same
area
Fig. 3. Membrane potential response to two pulse inputs. (flagS = 4) Simulation
4:
Spiking neuron
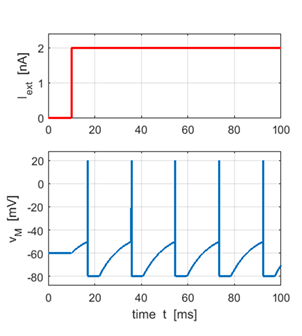
Fig. 4. An action potential is produced when the membrane potential reaches its threshold value. After the neuron has fired, the membrane potential is reset to the reset voltage. If Iext > 1.2 nA a spike is generated. (flagS = 4). Simulation 5: Spiking neuron with a step input A step input stimulus
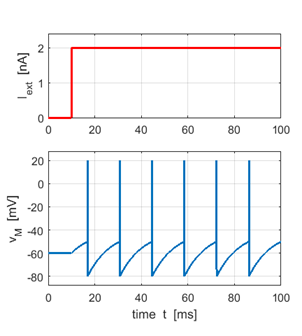
results in a continual firing of the neuron at regular intervals. In figure 5a,
the absolute refractory period is set to zero, whereas in figure 5b, the
refractory period is
Fig. 5a.
Time evolution of the membrane potential and the external current
input stimulus for a zero absolute refractory period.
Fig.
5b. Time evolution of the
membrane potential and the external current input stimulus for a non-zero
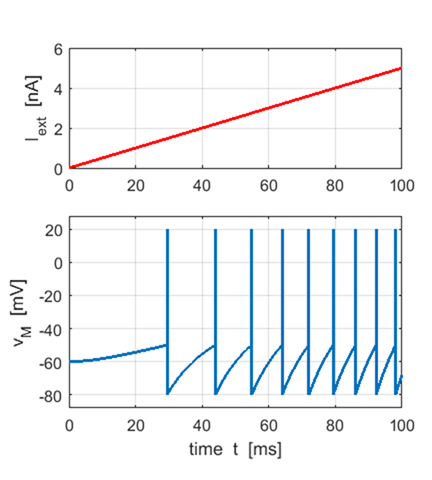
absolute refractory period. Simulation 6 A
ramp input stimulus produces action potentials with an increasing firing rate
as the input strength increases (figure 6 flagS
= 5)
Fig. 6a. Firing rate of neuron increases
as strength of the input stimulus increases. The absolute refractory period
is set to zero. Matlab Command Window Interspike times ISI [ms] 14.48 10.90 9.14 8.04 7.28 6.68 6.24 5.86 Neuron firing rate [Hz] 69.05 91.72 109.39 124.35 137.34 149.67 160.22 170.61 mean firing rate f = 126.54
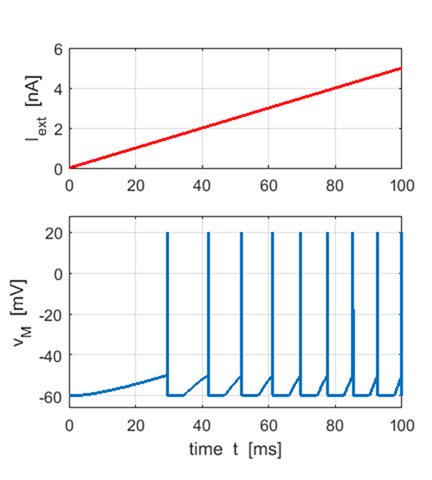
Fig. 6b. Firing rate of neuron increases
as strength of the input stimulus increases. A non-zero absolute refractory
period reduces the firing rate. Matlab Command Window Interspike times ISI [ms] 18.02 14.46 12.72 11.64 10.88 Neuron firing rate [Hz] 55.48 69.14 78.60 85.89 91.89 mean firing rate f = 76.20
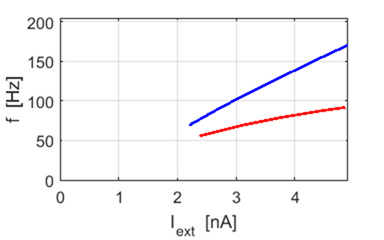
Fig. 6c. f – I curve for a LIF
neuron.
An action potential is not
produced until the external current exceeds a critical value which has a
value of about 1.5 nA. Simulation 7 Noisy input
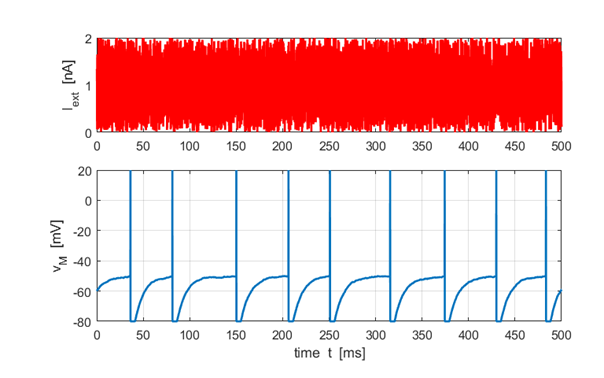
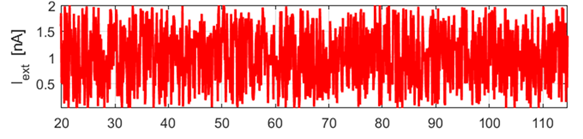
Fig. 7. The membrane potential response to a noisy input current stimulus. At each time step the external current is randomly assigned between 0 to 2.0 nA. The spike times are irregular. (flagS = 6) Simulation
8: Synaptic current
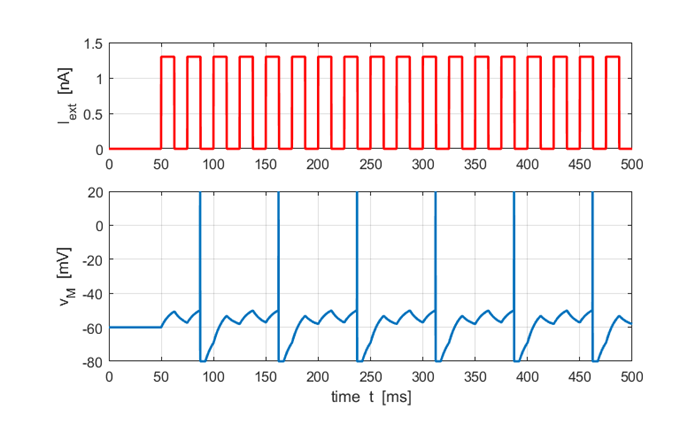
inputs Consider a more realistic situation where the neuron is stimulated by pre-synaptic spikes arriving at its synapses. The pre-synaptic spikes are linearly summed to give the input current and when the threshold voltage is reached, a spike is generated.
Fig. 8. Each pulse can be
considered as an input from a set of pre-synaptic junctions. |