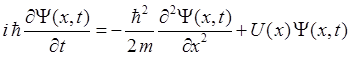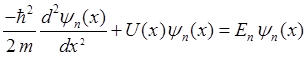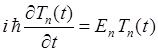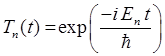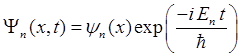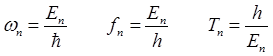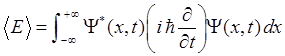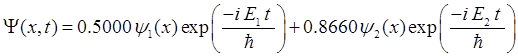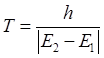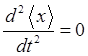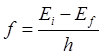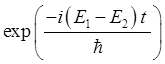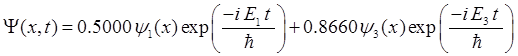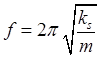|
|
QUANTUM PHYSICS SCHRODINGER EQUATION Time evolution of the
wavefunction - stationary and compound states Ian Cooper matlabvisualphysics@gmail.com DOWNLOAD
DIRECTORY FOR MATLAB SCRIPTS The Matlab scripts are used
to give the solution of the Schrodinger Equation for a variety of potential
energy functions using a matrix method where the solutions are the
eigenvalues and eigenfunctions of the energy
operator. Read the paper on the Matrix
Method before proceeding with this paper. se_wells.m First m-script to be run when solving the
Schrodinger Equation using the Matrix Method. Most of the constants and all
the well parameters are declared in this file. You can select the type of potential
well from the Command Window when the m-script is run. You alter the
m-script code to change the parameters that characterize the wells and you
can add to the m-script to define your own potential well. When this m-script
is run it clears all variables and closes all open Figure Windows. se_solve.m This m-script solves the Schrodinger Equation using the Matrix Method
after you have run the m-script se_wells.m. The eigenvalues
and corresponding eigenvectors are found for the bound states of the selected
potential well. se_stationary.m To be run after se_wells.m and se_solve.m. You can
investigate and view the time evolution of an energy eigenstate
and save the plot as an animated gif. se_super.m To be run after se_wells.m and se_solve.m. You can
investigate and view the time evolution of a compound state and save the plot
as an animated gif. STATIONARY STATES AND SUPERPOSITION
PRINCIPLE In wave
mechanics, the state of a system is described by a wavefunction that
satisfies the Schrodinger Equation and the boundary conditions imposed on the
system. For a one dimensional system, the Schrodinger Equation for a
potential energy function U(x) is
(1) We will
consider only those solutions that are described by a state of definite
energy by the method of separation of variables where the wavefunction is
expressed as
(2) The
substitution of this wavefunction into the Schrodinger Equation, gives two
ordinary differential equations and for quantum state n
(3)
(4) The
solution of the ordinary differential equation (4) is
(5) For stationary states which have
a definite total energy, the wavefunction is
(6) If the
energy of the system is measured, the value En will
certainly be obtained. This is a special type of solution of the Schrodinger
Equation. Applying Born’s rule, which states that the probability of
finding the particles in a small interval dx centered on x for
the state n is
Hence, the
probability is independent of time t and this is why it is called a stationary state. The real and imaginary
parts of the wavefunction change with time but not the modulus. All parts
oscillate in phase (like a stationary normal mode of a vibrating guitar
string). The concept of stationary states is not one that is familiar to us
in the classical world as nothing is moving at all, the probability of
detecting an electron in any given region never changes. All the expectation
value such as position, momentum and energy are also independent of time. Each stationary state wavefunction as described by
equation (6) describes a complex standing wave. A standing wave
is one that oscillates without propagation through space, with all points of
the standing wave vibrating in phase. The frequency and period of the
vibration are
The standing wave has nodes fixed in space. As n
increases, the total energy En and number of nodes
increases, while the period of vibration Tn
decreases. There is zero probability of locating the particle
bound in the well at each node. We can no longer think of the particle moving
from place to place in the well. In quantum physics, a particle has no
position until it is measured, so it makes no sense to think of the particle
moving about. There is no problem associated with the particle having to travel
through a nodal point, since the particle has no position and velocity. When
a measurement is made, it only tells us the position and velocity at the
instant after the measurement. Before the measurement, the state is simply
described by the wavefunction which gives us the most complete description
that is possible of the state of the system, but it does not give us
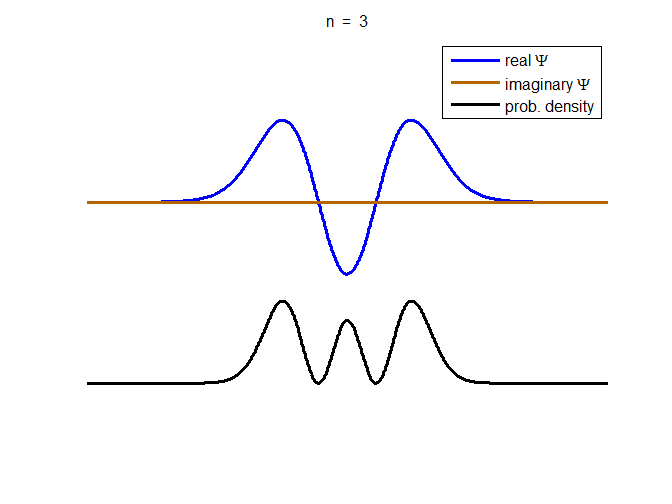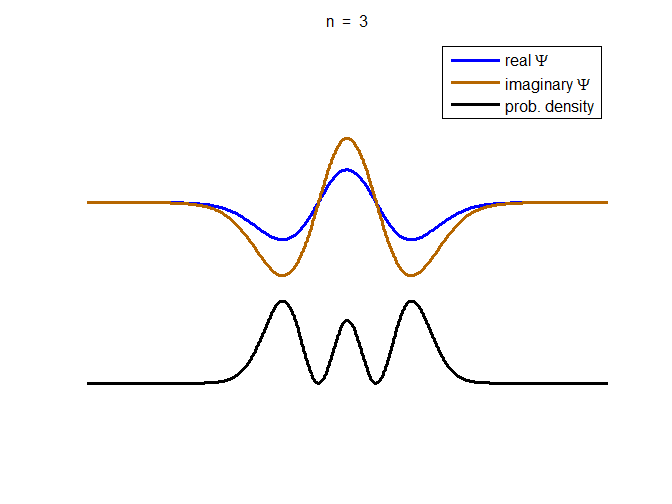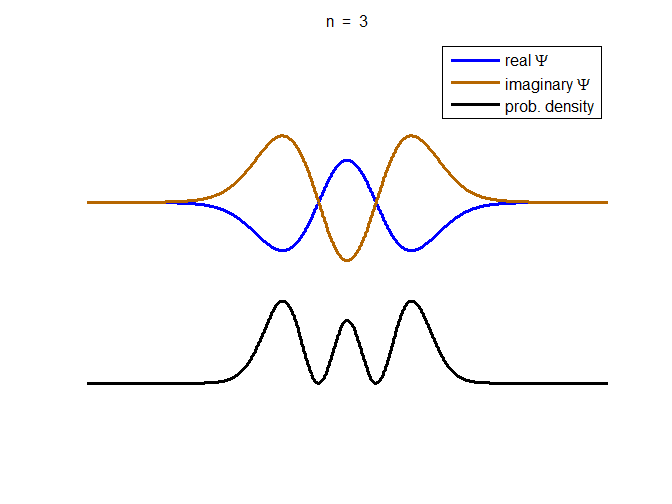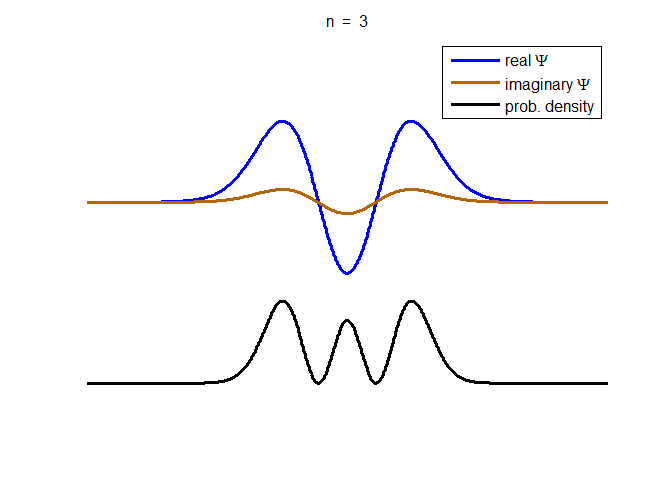
information about the position and velocity of the particle. Figure (1) show the time evolution for a number of
time steps of the real and imaginary parts of the wavefunction and the
probability density for the stationary state n = 3 of the truncated
harmonic oscillator. The phase of the real and imaginary parts change with
time but the probability density is independent of time.
Fig. 1. The time evolution of the wavefunction’s
real and imaginary parts for the stationary state n = 3 for a
truncated parabolic well. The probability density does not change with time.
[se_wells.m se_solve.m se_stationary.m] An animation of the changes with time of the
wavefunction can be observed by running the m-script se_stationary.m.
Fig. 2. An
animated gif of the time evolution of the stationary state n = 3 for a
truncated parabolic well. [se_stationary.m] Wavefunctions
have a very important property in that they obey the superposition
principle: If a set of
wavefunctions are solutions of the Schrodinger Equation, then any linear
combination of the wavefunctions is also a solution
If the
wavefunctions
The probability density of finding a particle in a
given length element dx is
When the particle is in an eigenstates
with a definite energy En then
and
so the probability distribution does not change with time as shown in figure
(1). Also, the expectation value for the position of the particle The expectation value for the total energy is
Using the
fact that the eigenfunctions are orthonormal
and doing
some algebra it is not difficult to show that the expectation value for the
total energy is
(7) Any
measurement of the total energy of the system will always give one of the
eigenvalues En and not Run
se_wells.m and se_solve.m
for the default truncated parabolic well: %
parabolic ***************************************************** case
5
xMin =
-0.2;
% default = -0. nm
xMax =
+0.2;
% default = +0.2 nm
x1 =
0.2;
% width default = 0.2 nm;
U1 =
-400;
% well depth default = -400 eV; The
energy eigenvalues for this potential well from se_solve.m
are: No. bound states found =
5 Quantum State /
Eigenvalues En (eV) 1
-360.92 2
-282.77 3
-204.68 4
-127.09 5
-52.272 The
m-script se_super.m adds any two of the eigenfunctions to form a compound state. To investigate
the addition of the eigenstates 1 and 2, in the
code for se_super.m enter qn(1) = 1; qn(2)
= 2; % states to be summed ac(1)
= 0.5; ac(2) = sqrt(1-ac(1)^2);
% coefficients to form the compound state
(8) The expectation value (eV) for
this compound state is displayed in the Command Window
Eavg_s =
-302.3036 see equation (7) Figure (3)
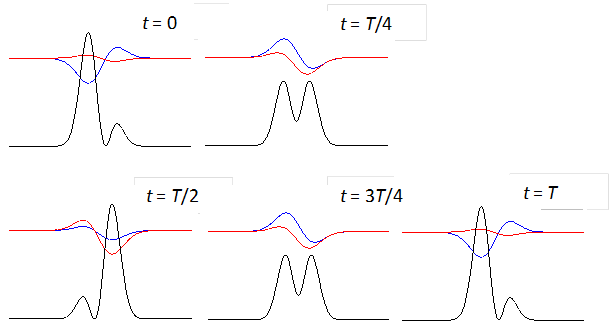
shows the time evolution of the compound state at times t = 0, T/4,
T/2, 3T/4, T where T
is the period of the oscillation of the wavefunction. The red curves are the
real parts and the blue curves the imaginary part of the compound
wavefunction. The black curves shows the variation
with time of the probability density. For the compound state where
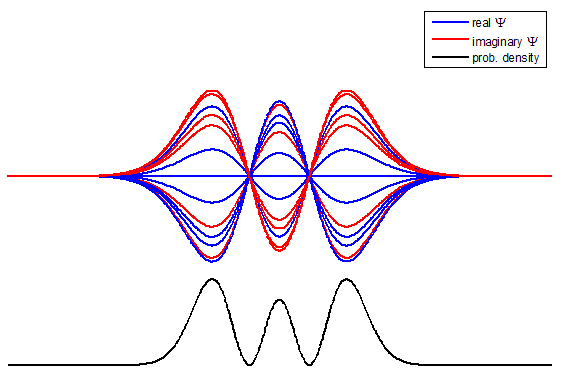
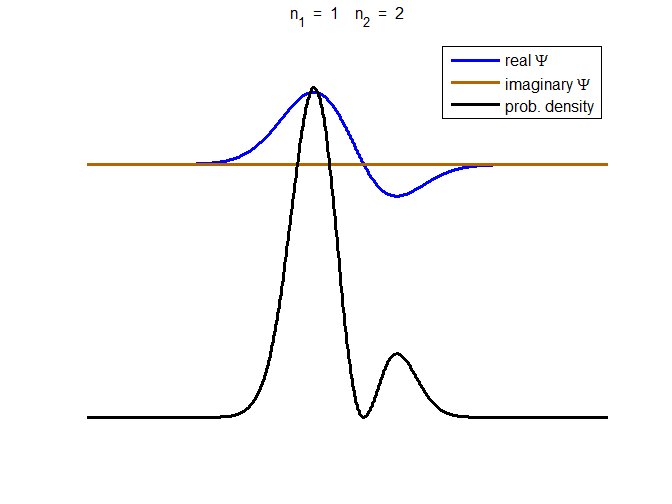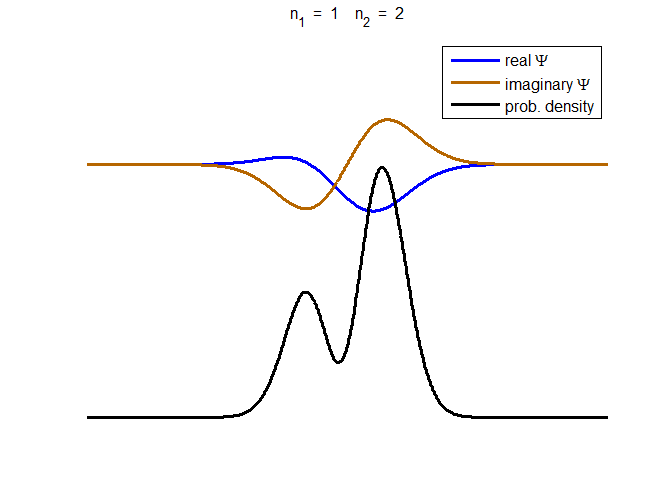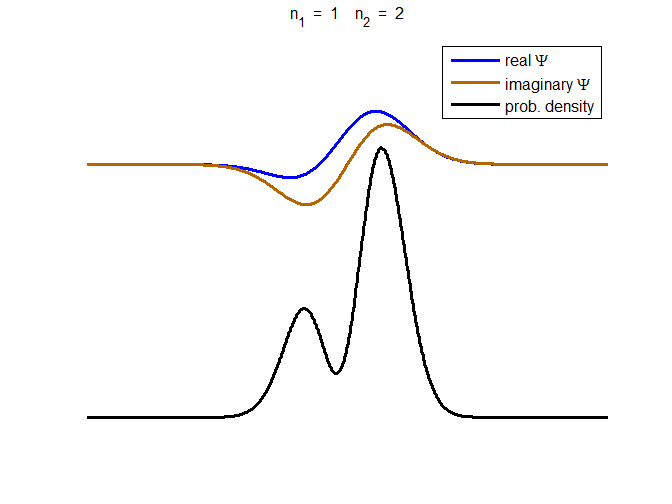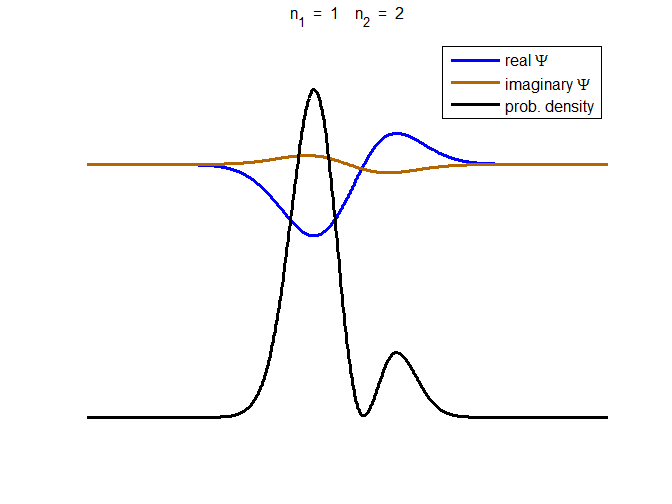
Fig. 3. The time evolution of the wavefunction’s
real and imaginary parts for a compound state given by equation (8) for a
truncated parabolic well. The probability density changes with time as the
charge distribution oscillates back and forward in the potential well. Red
curves – real part
[se_wells.m se_solve.m se_super.m]
Fig. 4. An animated gif of the time evolution of the compound state n
= 1 and n = 2 for a truncated parabolic well.
[se_super.m] Therefore,
the expectation of the position of the electron
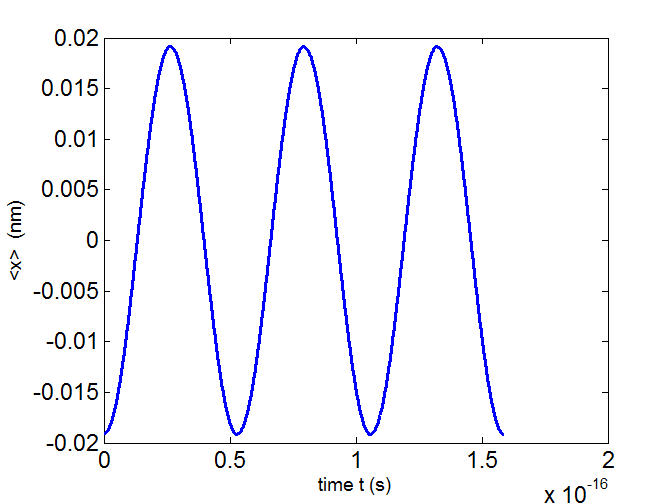
Fig. 5. The time variation of the expectation value for the
position of the electron
state n = 1 and n = 2 for a truncated
parabolic well. T = 5 .294×10-17 s.
[se_wells.m se_solve.m se_super.m] RADIATION EMITTED BY THE SYSTEM In
classical electromagnetism, an accelerated charge radiates electromagnetic
radiation at a rate that increases with its acceleration. In quantum
mechanics, the acceleration of a particle is not defined and an electron in a
given state does not radiate energy. But, we can explain the radiation due to
transitions between states using a semi-classical approach by considering the
expectation value
therefore,
So, a stationary state does not radiate. However,
the bound particle is not alone in the universe, sooner or later the particle
will interact with its surroundings (photon, or some other particle, etc), perturbing the energy so that the particle is no
longer in a stationary state. The particle will start in its initial
stationary state, absorb a photon for example, and then exist in a compound
state where the coefficients an are now time dependent. In the compound state, the system
does not have a definite energy and the expectation value
For the our
compound state in the harmonic potential well, the variation the expectation
values with time depends on the exponential term
and
the expectation value n
= 1, E1= - 360.92 eV. The values
of the frequency and wavelength of the emitted photon for the transition are:
n = 2 à
n = 1 Dn =
+1 f21 = 1.89×1016
Hz l21
= 1.59×10-8 m (UV) We will now
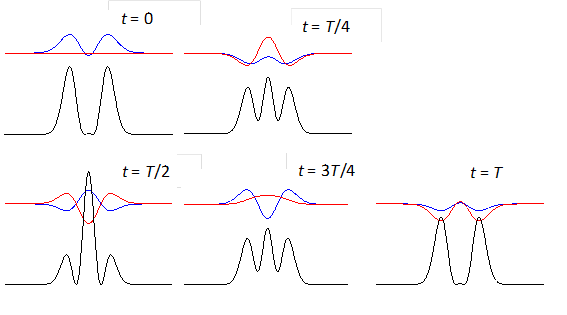
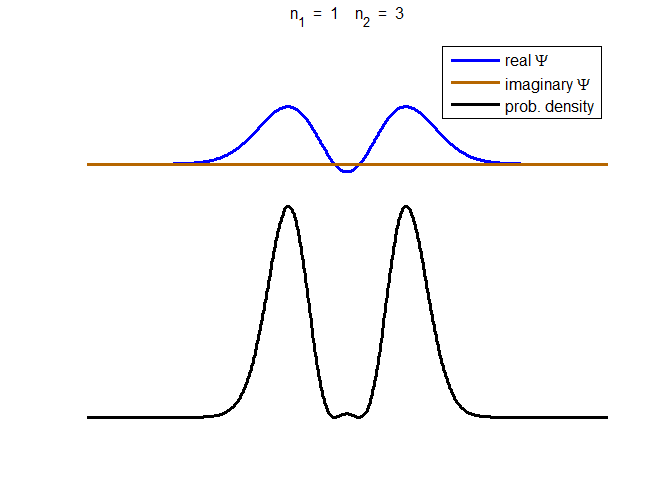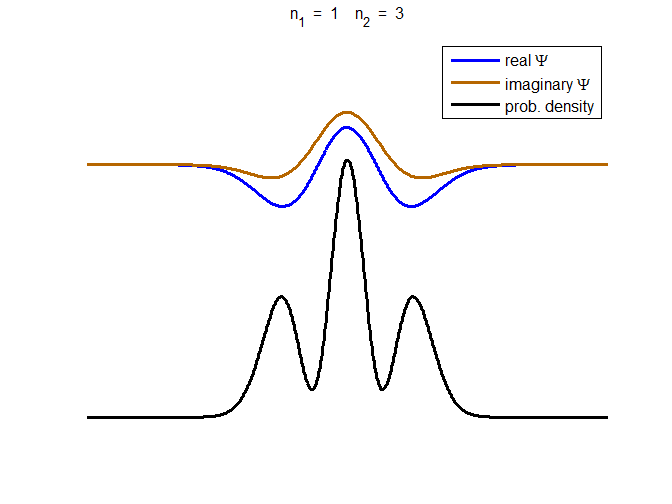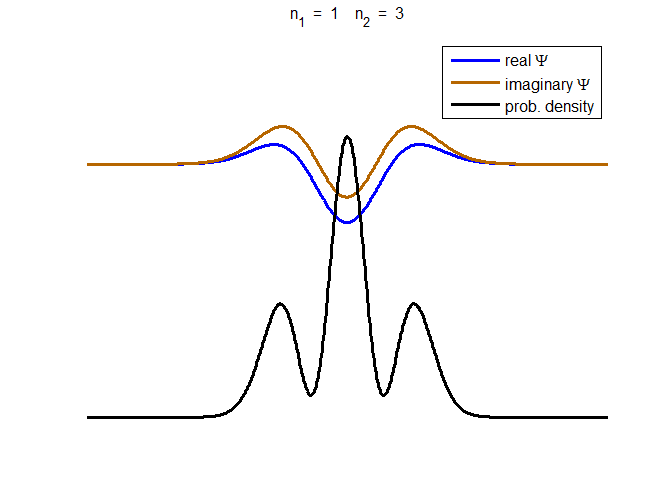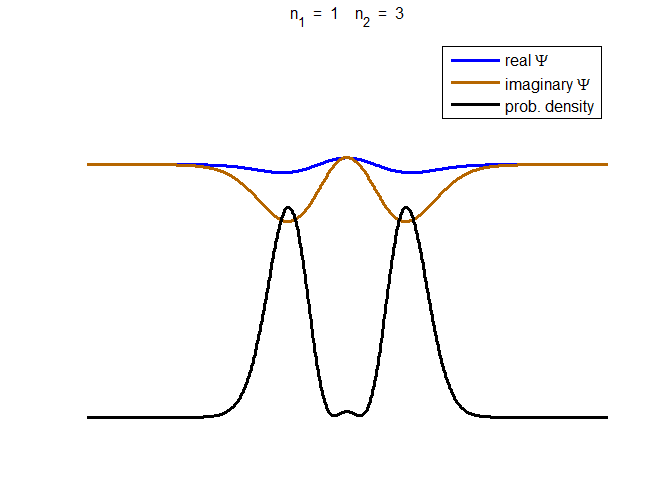
consider the compound state which is a summation of the two eigenstates n = 1 and n = 3
(9) The time
evolution of the real and imaginary parts of the wavefunction and the
probability density are shown in figure (6). However, even though the
probability density changes with time, there is no sloshing back and forward
and the expectation value for position as m
mass of particle ks
spring constant for system
Fig. 6. The time evolution of the wavefunction’s
real and imaginary parts for a compound state given by equation (9) for a
truncated parabolic well. The probability density changes with time as the
charge distribution oscillates back and forward in the potential well. Red
curves – real part
[se_wells.m se_solve.m se_super.m]
Fig. 7. An animated gif of the time evolution of the compound state n
= 1 and n = 3 for a truncated parabolic well.
The time variation of the expectation value for the position of the electronis [se_wells.m se_solve.m se_super.m]
Investigations Run se_wells.m, se_solve.m and then se_stationary.m and explore the
characteristics of the time evolution of stationary states. Determine the frequency
and period of the oscillations. Run se_wells.m, se_solve.m and then se_super.m and explore the
characteristics of compound wavefunctions. Select the
truncated harmonic potential well and verify that radiation is emitted only
for transitions where |
|