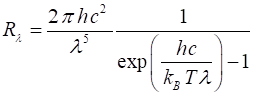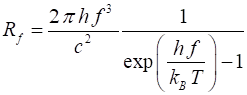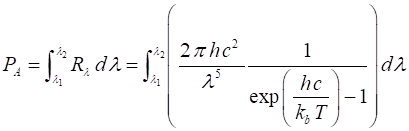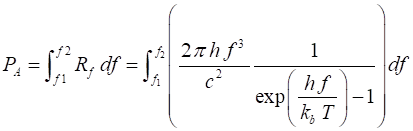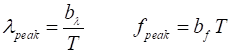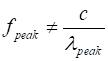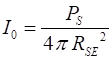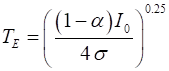DOING PHYSICS WITH MATLAB

SOLAR RADIATION MODELLING

BLACKBODY RADIATION

Ian Cooper

matlabvisualphysics@gmail.com

DOWNLOAD DIRECTORIES FOR MATLAB SCRIPTS

Google drive

GitHub

tpSun.m

Simulation of the electromagnetic radiation emitted from the Sun. The Script can be used to create colour spectrums of the radiation emitted from the Sun by calling the Script Colorcode.m.

solarData.mat

Solar spectrum data for the effects of the atmosphere of the radiation reaching the ground: AM0 and AM1.5.

simpson1d.m

Function to evaluate the area under a curve using Simpson’s 1/3 rule.

ColorCode.m

Function to return the appropriate colour for a wavelength in the visible range from 380 nm to 780 nm.

BLACKBODY RADIATION

PARTICLE NATURE OF ELECTROMAGNETIC RADIATION

The goal of this article to investigate the solar spectrum: the Sun as a blackbody and the calculation of the intensity of solar irradiance at the Earth's surface.

The wave nature of electromagnetic radiation is demonstrated by interference phenomena. However, electromagnetic radiation also has a particle nature. For example, to account for the observations of the radiation emitted from hot objects, it is necessary to use a particle model, where the radiation is considered to be a stream of particles called photons. The energy of a photon, E is

(1)

The electromagnetic energy emitted from an object’s surface is called thermal radiation and is due to a decrease in the internal energy of the object. This radiation consists of a continuous spectrum of frequencies extending over a wide range. Objects at room temperature emit mainly infrared and it is not until the temperature reaches about 800 K and above those objects glows visibly.

A blackbody is an object that completely absorbs all electromagnetic radiation falling on its surface at any temperature. It can be thought of as a perfect absorber and emitter of radiation. The power emitted from a blackbody, P is given by the Stefan-Boltzmann law and it depends only on the surface area of the emitter, A and its surface temperature, T

(2)

A more general form of equation (2) is

(2)

where e is the emissivity of the object. For a blackbody, e = 1. When e < 1 the object is called a graybody and the object is not a perfect emitter and absorber.

The amount of radiation emitted by a blackbody is given by Planck’s radiation law and is expressed in terms of the spectral exitance for wavelength or frequency R_l or R_f respectively

(4) [W.m^-2.m^-1]

or

(5) [W.m^-2.s^-1]

The spectral exitance is also called the spectral irradiance [W.m^-2.m^-1].

In the literature, many different terms and symbols are used for the spectral exitance. Sometimes the terms and the units given are wrong or misleading. Note units for equation 1: The units in the denominator should be thought of in terms of m².m where the first factor m² corresponds to the surface area of the blackbody and the second unit of length m corresponds to the wavelength of the emitted light.

The power radiated per unit surface of a blackbody, P_A within a wavelength interval or bandwidth, (l₁, l₂) or frequency interval or bandwidth (f₁, f₂) are given by equations 6 and 7

(6) [W.m^-2]

and

(7) [W.m^-2]

The equations 6 and 7 give the Stefan-Boltzmann law (equation 2) when the bandwidths extend from 0 to ¥.

Wien’s Displacement law states that the wavelength l_peak corresponding to the peak of the spectral exitance given by equation 4 is inversely proportional to the temperature of the blackbody and the frequency f_peak for the spectral exitance peak frequency given by equation 5 is proportional to the temperature

(8)

The peaks in equations 4 and 5 occur in different parts of the electromagnetic spectrum and so

(9)

The Wien’s Displacement law explains why long wave radiation dominates more and more in the spectrum of the radiation emitted by an object as its temperature is lowered.

When classical theories were used to derive an expression for the spectral exitances R_l and R_f, the power emitted by a blackbody diverged to infinity as the wavelength became shorter and shorter. This is known as the ultraviolet catastrophe. In 1901 Max Planck proposed a new radical idea that was completely alien to classical notions, electromagnetic energy is quantized. Planck was able to derive the equations 4 and 5 for blackbody emission and these equations are in complete agreement with experimental measurements. The assumption that the energy of a system varies in a continuous manner, i.e., (take any arbitrary close consecutive values fails. Energy can only exist in integer multiples of the lowest amount or quantum, h f.

This step marked the very beginning of modern quantum theory.

A summary of the physical quantities, units and values of constants used in the description of the radiation from a hot object.

Variable	Interpretation	Value	Unit
E	energy of photon		J
h	Planck’s constant	6.62608´10^-34	J.s
c	speed of electromagnetic radiation	3.00x10^8	m.s^-1
f	frequency of electromagnetic radiation		Hz
l	wavelength of electromagnetic radiation
T	surface temperature of object		K
A	surface area of object		m^2
s	Stefan-Boltzmann constant	5.6696´10^-8	W.m^-2.K-4
P	power emitted from hot object		W
e	emissivity of object’s surface
Rl	spectral exitance: power radiated per unit area per unit wavelength interval		(W.m^-2).m^-1
Rf	spectral exitance: power radiated per unit area per unit frequency interval		(W.m^-2).s^-1
kB	Boltzmann constant	1.38066´10^-23	J.K^-1
bl	Wien constant: wavelength	2.898´10^-3	m.K
bf	Wien constant: frequency	2.83 kB T / h	K^-1.s-1
lpeak	wavelength of peak in solar spectrum	5.0225´10^-7	m
RS	radius of the Sun	6.96´10^8	m
RE	radius of the Earth	6.96´10^6	m
RSE	Sun-Earth radius	6.96´10^11	m
I0	Solar constant	1.36´10^3	W.m^-2
a	Albedo of Earth’s surface	0.30

THE SUN AS A BLACKBODY

The Sun can be considered as a blackbody, and the total power output of the Sun P_S can be estimated by using the Sefan-Boltzmann law, equation 2, and by finding the area under the curves for R_l and R_f using equations 6 and 7. From observations on the Sun, the peak in the electromagnetic radiation emitted has a wavelength, l_peak = 502.25 nm (green). The temperature of the Sun’s surface (photosphere) can be estimated from the Wien displacement law, equation 8.

The distance from the Sun to the Earth, R_SE can be used to estimate of the surface temperature of the Earth T_E if there was no atmosphere. The intensity of the Sun’s radiation reaching the top of the atmosphere, I₀ is known as the solar constant

(10)

The power absorbed by the Earth, P_Eabs is

(11)

where a is the albedo (the reflectivity of the Earth’s surface). Assuming the Earth behaves as a blackbody then the power of the radiation emitted from the Earth, P_Erad is

(12)

It is known that the Earth’s surface temperature has remained relatively constant over many centuries, so that the power absorbed and the power emitted are equal, so the Earth’s equilibrium temperature T_E is

(13)

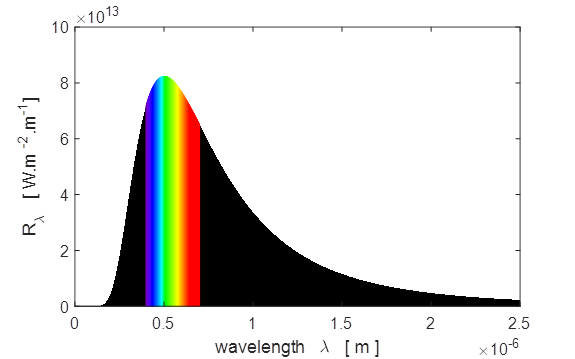
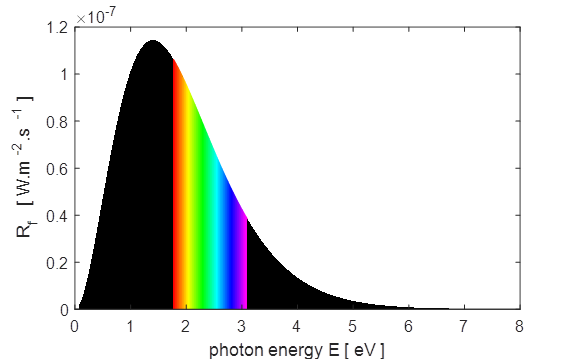
The Script tpSun.m can be used to calculate and plot details of the Sun and Earth as blackbodies. The results of the computation are displayed in the Command Window and Figure Windows. Plots of the spectral exitance curves for the Sun as shown in figure 1.

Fig. 1. Plots of the spectral exitance curves as a function of wavelength and photon energy . The two peaks occur in different parts of the electromagnetic spectrum . The visible spectrum falls approximately in the wavelength range from 700 nm to 400 nm. The peak occurs in the green part of the visible spectrum . tpSun.m

Matlab screen output for tpSun.m

Sun: temperature of photosphere, T_S = 5770 K

Peak in Solar Spectrum

Theory: Wavelength at peak in spectral exitance, wL = 5.02e-07 m

Graph: Wavelength at peak in spectral exitance, wL = 5.04e-07 m

Corresponding frequency, f = 5.95e+14 Hz

Theory: Frequency at peak in spectral exitance, f = 3.39e+14 Hz

Graph: Frequency at peak in spectral exitance, f = 3.40e+14 Hz

Corresponding wavelength, wL = 8.82e-07 m

Total Solar Power Output

P_Stefan_Boltzmann = 3.79e+26 W

P(wL)_total = 3.77e+26 W

P(f)_total = 3.79e+26 W

IR visible UV

P_IR = 1.92e+26 W

Percentage IR radiation = 51.0

P_visible = 1.39e+26 W

Percentage visible radiation = 36.8

P_UV = 4.61e+25 W

Percentage UV radiation = 12.2

Sun - Earth

Theory: Solar constant I_O = 1.360e+03 W/m^2

Computed: Solar constant I_E = 1.342e+03 W/m^2

Surface temperature of the Earth, T_E = 254 K

Surface temperature of the Earth, T_E = -19 deg C

M-script highlights

1 Suitable values for the wavelength and frequency integration limits for equations (6) and (7) are determined so that the spectral exitances at the limits are small compared to the peak values.

2 The Matlab function area is used to plot the spectral exitance curves, for example, in plotting the R_l curve:

h_area1 = area(wL,R_wL);

set(h_area1,'FaceColor',[0 0 0]);

set(h_area1,'EdgeColor','none');

3 The color for the shading of the curve matches that of the wavelength in the visible part of the spectrum. A call is made to the function ColorCode.m to assign a color for a given wavelength band. For the shading of the R_l curve:

thisColorMap = hsv(128);

for cn = 1 : num_wL-1

thisColor = ColorCode(wL_vis(cn));

h_area = area(wL_vis(cn:cn+1),R_wL_vis(cn:cn+1));

set(h_area,'FaceColor',thisColor);

set(h_area,'EdgeColor',thisColor);

4 Simpson’s 1/3 rule is used for the numerical integration (simpson1d.m) to find the area under the spectral intensity curves. For the R_l curve, the total power radiated by the Sun:

P_total = A_sun * simpson1d(R_wL,wL1,wL2);

5 The peaks in spectral intensities are calculated using Matlab logical functions:

wL_peak_graph = wL(R_wL == max(R_wL));

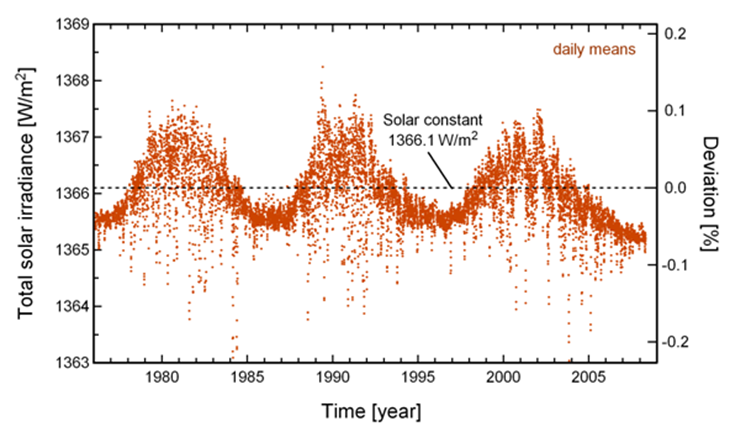
f_peak_graph = f(R_f == max(R_f));

SOLAR CONSTANT

The flux of solar radiation energy that arrives at the outermost layers of the atmosphere is called the total solar irradiance. It varies slightly in an annual cycle because the Earth revolves around the Sun on an elliptic orbit (figure 2). The data show very slight variations (by about 0.1%) due to the 11-year solar cycle. The long-term average of the total solar irradiance is called the solar constant . The solar constant has changed by less than 0.2 W.m^-2 (0.015%) over the past 1000 years, hence the relatively small climate variations observed over this period of time.

Fig. 2. Each red dot plots the daily mean of the total solar irradiance measured at vertical incidence above the Earth’s atmosphere by satellites. The dashed line plots the long-term average of the solar constant . Source PV Lighthouse

The value of the solar constant is calculated in the Script tpSun.m

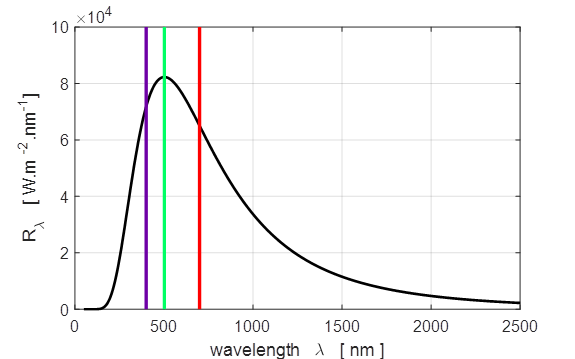
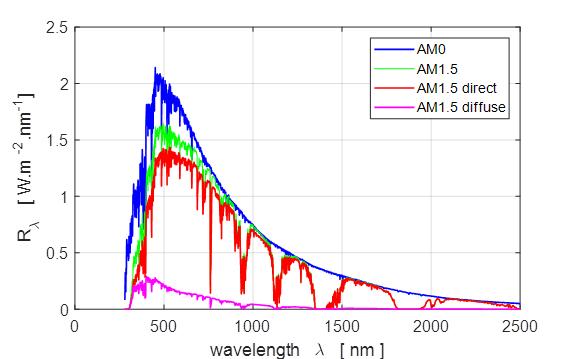
Theory: Solar constant I_O = 1.360e+03 W.m^-2

Computed: Solar constant I_E = 1.342e+03 W.m^-2

The extraterrestrial (AM0) solar spectrum

The energy of sunlight is called intensity or irradiance. Figure 3 shows the blackbody curve for the Sun at a temperature of 5770 K, and the spectral exitance curves measured above the top regions of the Earth’s atmosphere (AMO blue line), and the curves for AM1.5 (AM1.5 green line, direct radiation red line, diffuse radiation magenta line).

The acronym AM0 stands for the spectrum for air mass zero, meaning that the spectrum was measured with no air between the Sun and the detector. AM Air Mass

Fig, 3. Blackbody curve for the Sun at a temperature of 5770 K (top plot). The spectral irradiance curves AM0 and AM1.5 (bottom plot). The data for the curves in the bottom plot was downloaded as an Excel file by searching solar spectral irradiance data ASTM G-173.

tpSun.m Data file SolarData.mat

Note sure why the vertical scale of the top and bottom plots are so different in magnitude?

The Earth's atmosphere has a large impact upon the solar radiation reaching the surface of the Earth. The AM0 spectrum applies only to the top of the atmosphere. At the surface of the Earth, the solar spectrum is very different and cannot be approximated by the AM0 spectrum or the black body spectrum. The terrestrial solar spectrum is variable, as we know from daily life: the Sun changes color and intensity all the time.

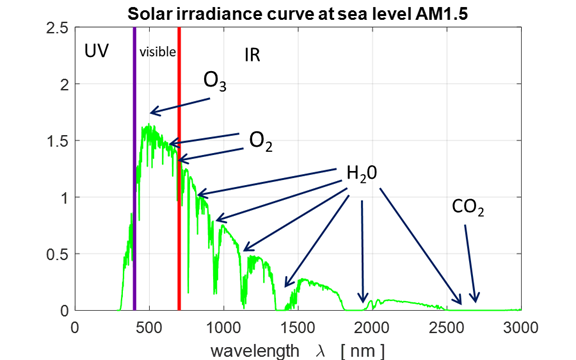
The following are the main mechanism for this spectral change:

· Absorption of radiation due to molecules and particles in the Earth atmosphere: water vapor, carbon dioxide, methane and other greenhouse gases mostly in the infrared region and by ozone in the visible and ultraviolet portion of the spectrum.

· Absorption and scattering by clouds.

· Scattering of radiation by molecules and particles in the atmosphere. Scattering of mainly blue light by dust and ice particles in the atmosphere, giving rise to direct and diffuse components.

· Reflection of radiation from the Earth surface.

· The mass of air the light must travel through which depends on the elevation of the Sun over the horizon.

The
absorption of solar radiation by molecules can be measured, and standardized tables are available on the internet corresponding to passage of the Sun's radiant energy through the equivalent of 1.5 clear atmospheres (AM1.5: the equivalent of 1.5 air masses). Note that AM1.5 has become a standard method of characterizing spectral irradiance for the design of photovoltaic systems.

Fig. 4. Simply diagram of the absorption of solar radiation by greenhouse gases.