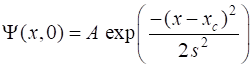DOING PHYSICS WITH PYTHON

QUANTUM MECHANICS

TIME DEPENDENT SCHRODINGER EQUATION

FINITE DIFFERENCE TIME DEVELOPMENT METHOD

WAVEPACKET SPREADING

Ian Cooper

matlabvisualphysics@gmail.com

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

qm002.py

GitHub

Google Drive

[1D] time dependent Schrodinger Equation using the Finite Difference Time Development Method (FDTD). link

WAVE-PACKET SPREADING

As an example, in solving the [1D] time dependent Schrodinger equation for a free particle, let’s consider an initial state described by the Gaussian function

where A is a normalized constant and is calculated so that , x_c is the centre of the Gaussian wavepacket and s determines its width. The time evolution of the wavepacket is found from its initial state by solving the [1D] time dependent Schrodinger Equation using the Finite Difference Time Development Method.

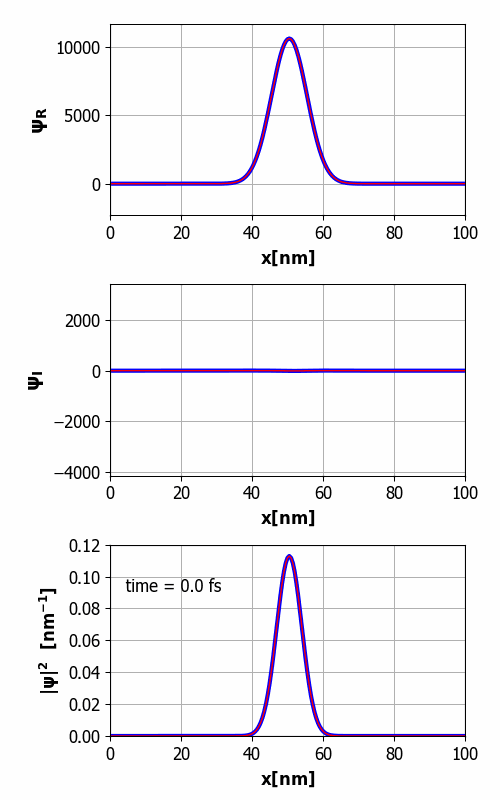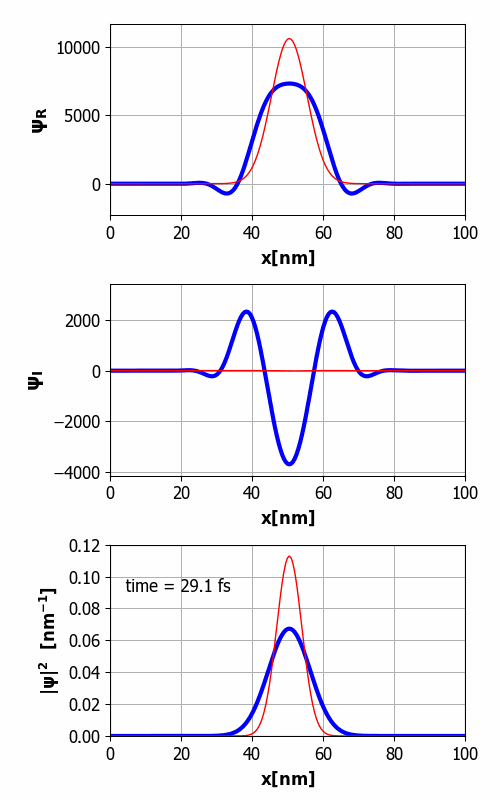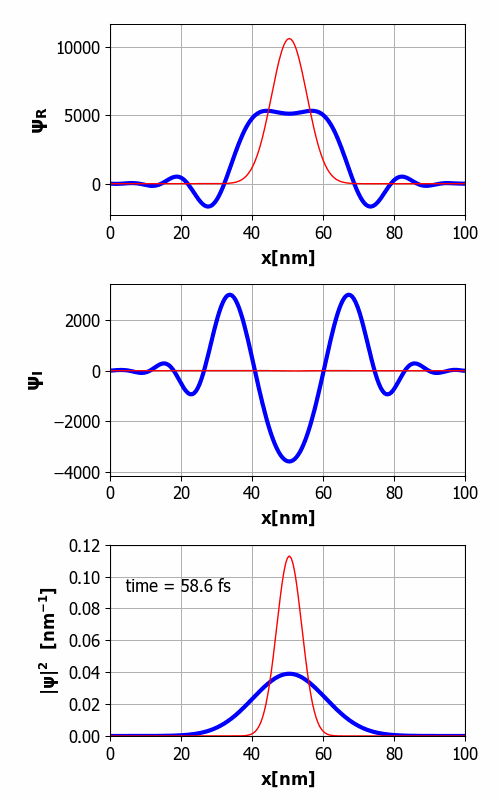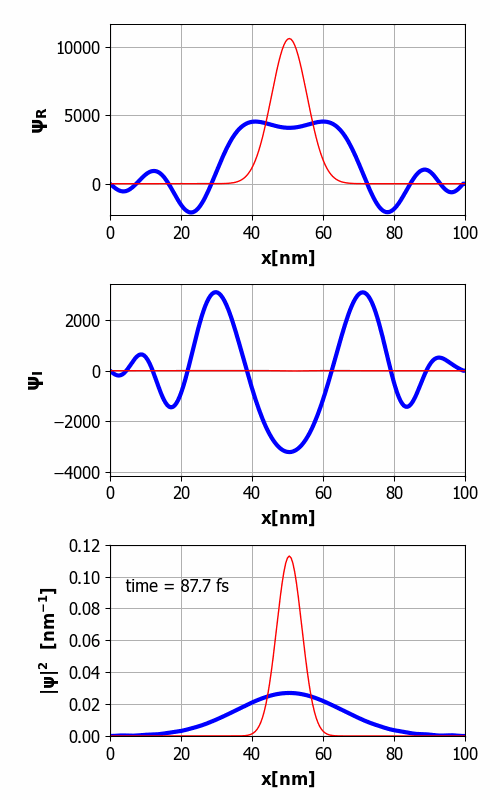
An animation of the time evolution of the wavepacket is shown in figure 1.

Fig. 1. Animation of the wavepacket from its initial state. The top graph shows the real part of the wavefunction, the middle graph the imaginary part, and the bottom graph, the probability density. You will notice that the width of the wavepacket grows with time, i.e., wavepacket spreading.

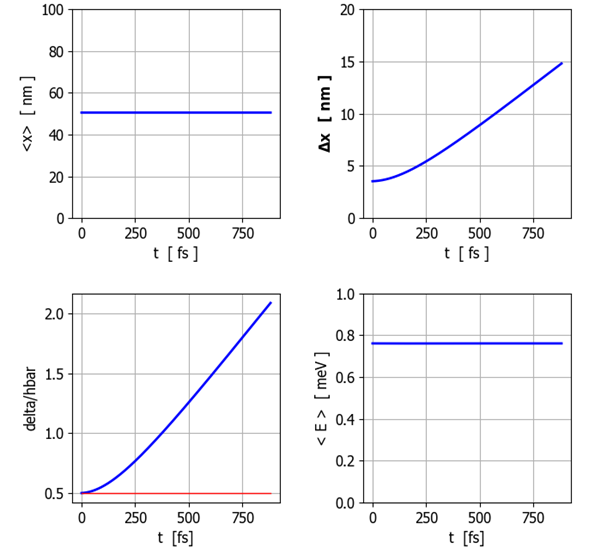
Although, the wavefunction develops real and imaginary parts, both of which have lots of wiggles, the probability density turns out to be another Gaussian function with a width that increases with time. Eventually, the width of the wavepacket is proportional to time (figure 2). The initial wavefunction has a spread of momentum and this distribution of momentum remains constant for a free particle because there are zero forces to change it. Since there is a spread in possible momenta, there is also a spread in velocities . This spread in velocities gives rise to the uncertainty in position of the particle that increases with time.

Fig. 2. The uncertainties in the position and momentum , and the product of the uncertainties . The Heisenberg Uncertainty Principle is satisfied since .

The wavepacket does not propagate since the initial velocity of the wavepacket is zero, it only spreads since there are zero forces acting on the particle. So, the expectation values of momentum, total energy, kinetic energy and potential energy are constants, independent of time. Hence, the wavepacket cannot move through space, it can only expand.