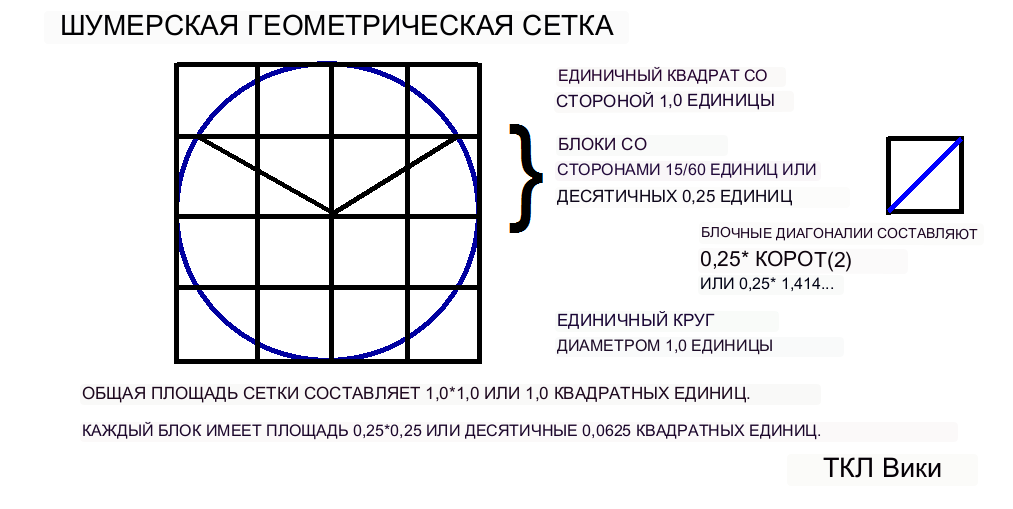
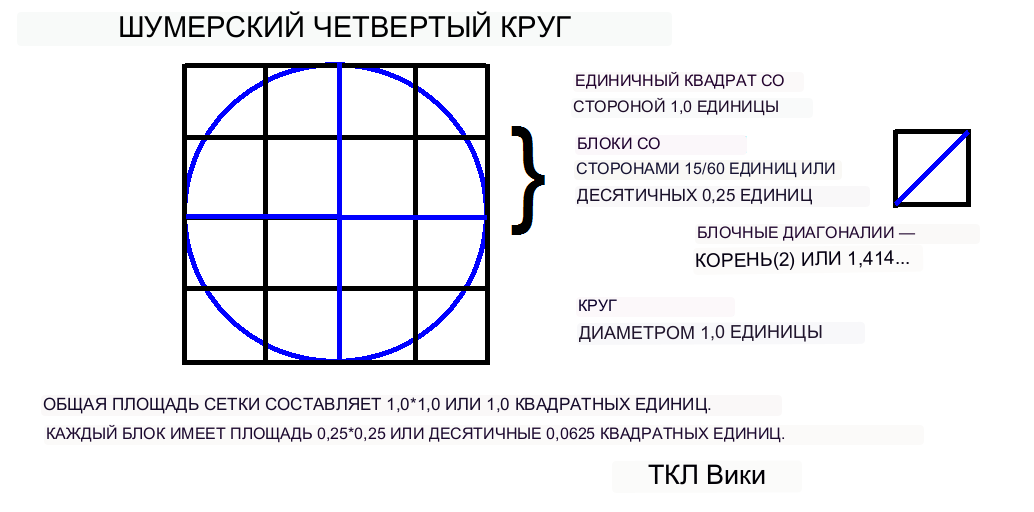
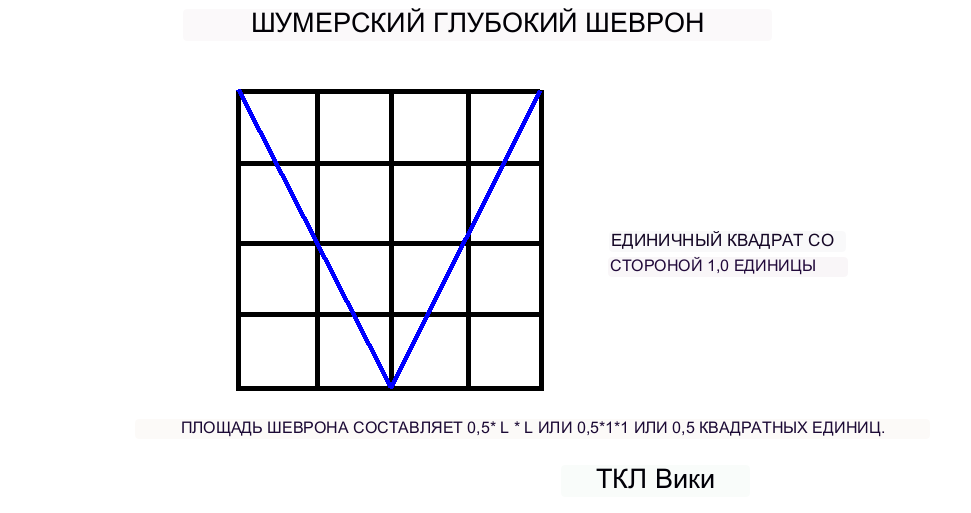
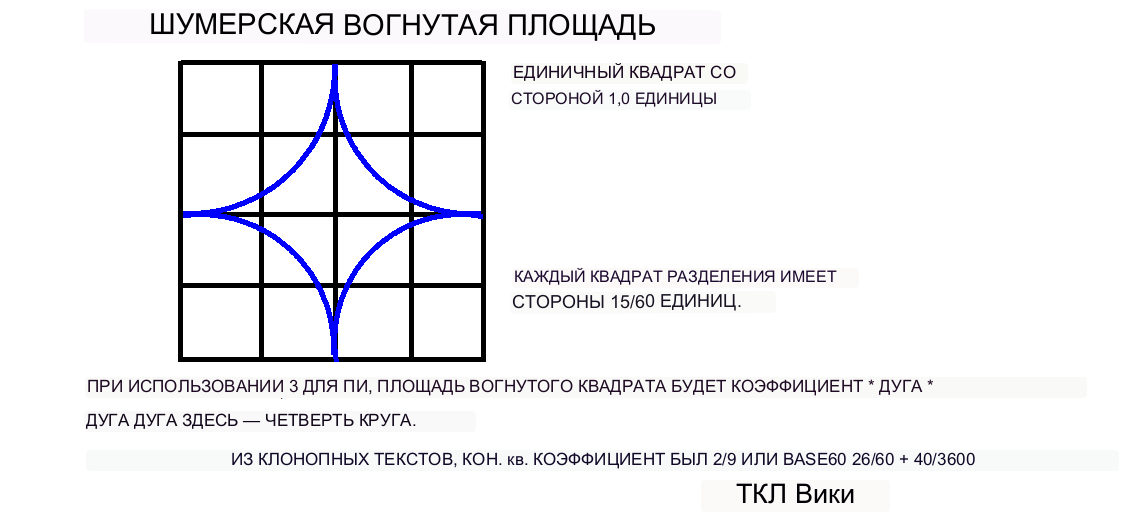
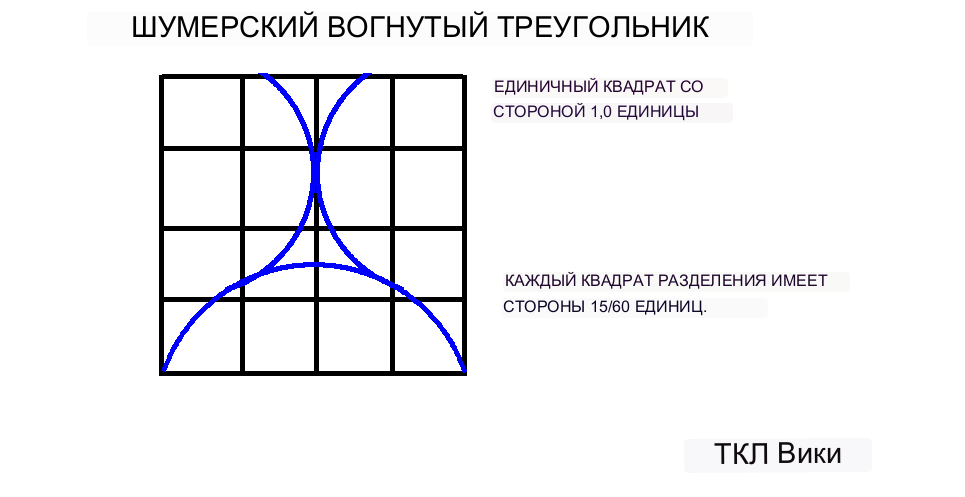
Предыдущие публикации Ваймана (1963), Фон Слодена (1964) и Робинсона (1999) показали, что большинство шестидесятеричных коэффициентов лука были получены из сегмента круга со углом 120 градусов и диаметром 1 единица. Далее единичный круг накладывался на квадратную сетку размером 1 на 1 единицу. Квадратную сетку можно разбить либо на 4 вертикальные полосы шириной 15/60 и высотой 1, либо на 16 квадратов со стороной 15/60. Первоначальные сегменты или фигурки лука содержались в вертикальных полосах шириной 15/60 и высотой 1. На планшете BM15285 на некоторых рисунках показаны отметки компаса и отметки построения линий частично стертой сетки из 16 квадратов. BM15285-p14 показывает сетку из 16 квадратов как математическую задачу о том, какова площадь разделенного квадрата. На глине линии надреза можно стереть, потерев их влажным большим пальцем. Помимо следов строительства, сетку из 16 квадратов можно получить из некоторых фигур, которые либо следуют линиям сетки, либо расположены внутри подквадратов или полос, например BM15285-p31, p32 и p34. На BM15285 стороны больших квадратов составляют 48 мм, а диаметр большинства кругов — 22 мм. За годы современной эпохи, с тех пор как были обнаружены таблички, было несколько замечаний о том, что конструкции квадратов, кругов и перекошены или не перпендикулярны. Учитывая небольшой масштаб конструкций и среду, конструкции имеют достаточно квадратную форму и близки по масштабу к старым печатным схемам 1970-х годов. До изобретения языка Postscript большинство современных книжных дизайнов рисовались на чертежном столе и уменьшались фотографически. например BM15285-p31, p32 и p34. На BM15285 стороны больших квадратов составляют 48 мм, а диаметр большинства кругов — 22 мм. За годы современной эпохи, с тех пор как были обнаружены таблички, было несколько замечаний о том, что конструкции квадратов, кругов и перекошены или не перпендикулярны. Учитывая небольшой масштаб конструкций и среду, конструкции имеют достаточно квадратную форму и близки по масштабу к старым печатным схемам 1970-х годов. До изобретения языка Postscript большинство современных книжных дизайнов рисовались на чертежном столе и уменьшались фотографически. например BM15285-p31, p32 и p34. На BM15285 стороны больших квадратов составляют 48 мм, а диаметр большинства кругов — 22 мм. За годы современной эпохи, с тех пор как были обнаружены таблички, было несколько замечаний о том, что конструкции квадратов, кругов и перекошены или не перпендикулярны. Учитывая небольшой масштаб конструкций и среду, конструкции имеют достаточно квадратную форму и близки по масштабу к старым печатным схемам 1970-х годов. До изобретения языка Postscript большинство современных книжных дизайнов рисовались на чертежном столе и уменьшались фотографически. было несколько замечаний, что конструкции квадратов и кругов перекошены или не перпендикулярны. Учитывая небольшой масштаб конструкций и среду, конструкции имеют достаточно квадратную форму и близки по масштабу к старым печатным схемам 1970-х годов. До изобретения языка Postscript большинство современных книжных дизайнов рисовались на чертежном столе и уменьшались фотографически. было несколько замечаний, что конструкции квадратов и кругов перекошены или не перпендикулярны. Учитывая небольшой масштаб конструкций и среду, конструкции имеют достаточно квадратную форму и близки по масштабу к старым печатным схемам 1970-х годов. До изобретения языка Postscript большинство современных книжных дизайнов рисовались на чертежном столе и уменьшались фотографически.
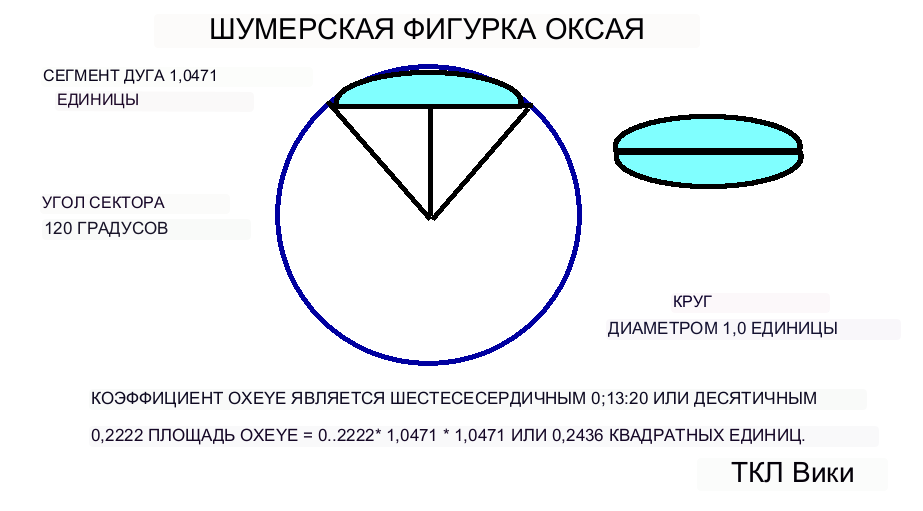
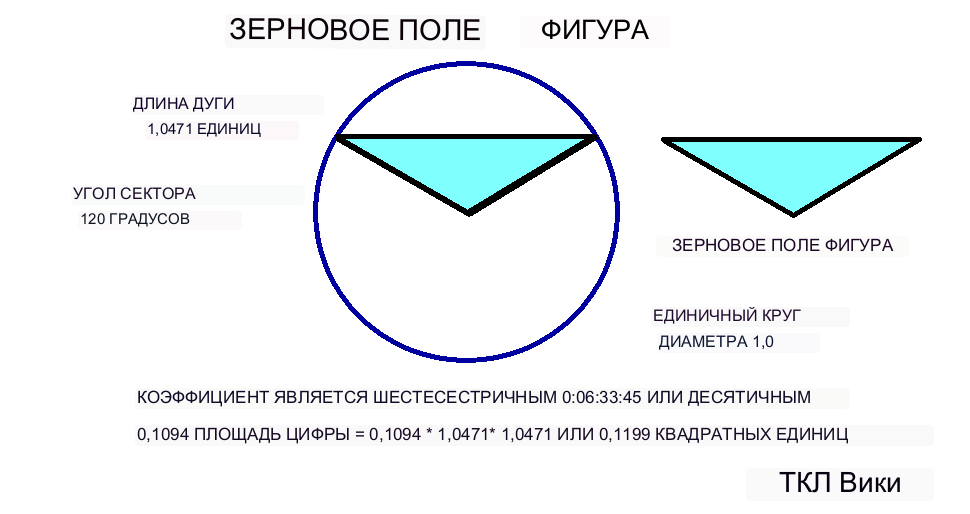
В шумерской геометрии построение кругового сегмента со стороной 120 градусов на единичной окружности приводит к образованию треугольника с двумя равными сторонами, кругового сегмента и подразумеваемой длины дуги этого сегмента. Носовая фигура представляет собой один сегмент, а фигура баржи — двойной сегмент. Фигуру треугольника называют фигурой хлебного поля от треугольников, используемых при межевании. Длина дуги кругового сегмента использовалась в качестве эталонной длины для расчета площади геометрических фигур с использованием различных коэффициентов. Одним из заданных наборов образующих коэффициентов был шестидесятеричный коэффициент поперечного сечения носовой части 0;52,30, коэффициент площади носовой части 0;6:33:15 и образующий радиус носовой части 0;30. Когда образующий радиус десятичных 0,5 отмечен от центра сетки, граница концевой полосы 15/60 будет определять длинную поперечную длину лука или тетивы. Ширина или короткое поперечное сечение лука 0,5-(15/60) или 0,25. Получится два прямоугольных треугольника со сторонами 15/60 и 30/60. По теореме Пифагора оставшаяся сторона равна sqrt((30/60)**2 + (15/60**2)), что составляет 26/60. Длина тетивы составляла 2*(26/60), что равно 52/60 или шестидесятеричной дроби 0;26 или десятичной дроби 0,866. Площадь фигуры лука будет равна площади сечения в 120 градусов минус площадь объединенных треугольников. При вычислении (1/3)*pi*(.5**2)-2*((1/2)*((15/60)*(26/60)) будет десятичной дробью 0,26179 - 0,108330 или десятичной дробью 0,15346. Калькулятор eTCL дает площадь лука в десятичных единицах 0,1535 квадратных единиц. Длина тетивы составляла 2*(26/60), что равно 52/60 или шестидесятеричной дроби 0;26 или десятичной дроби 0,866. Площадь фигуры лука будет равна площади сечения в 120 градусов минус площадь объединенных треугольников. При вычислении (1/3)*pi*(.5**2)-2*((1/2)*((15/60)*(26/60)) будет десятичной дробью 0,26179 - 0,108330 или десятичной дробью 0,15346. Калькулятор eTCL дает площадь лука в десятичных единицах 0,1535 квадратных единиц. Длина тетивы составляла 2*(26/60), что равно 52/60 или шестидесятеричной дроби 0;26 или десятичной дроби 0,866. Площадь фигуры лука будет равна площади сечения в 120 градусов минус площадь объединенных треугольников. При вычислении (1/3)*pi*(.5**2)-2*((1/2)*((15/60)*(26/60)) будет десятичной дробью 0,26179 - 0,108330 или десятичной дробью 0,15346. Калькулятор eTCL дает площадь лука в десятичных единицах 0,1535 квадратных единиц.
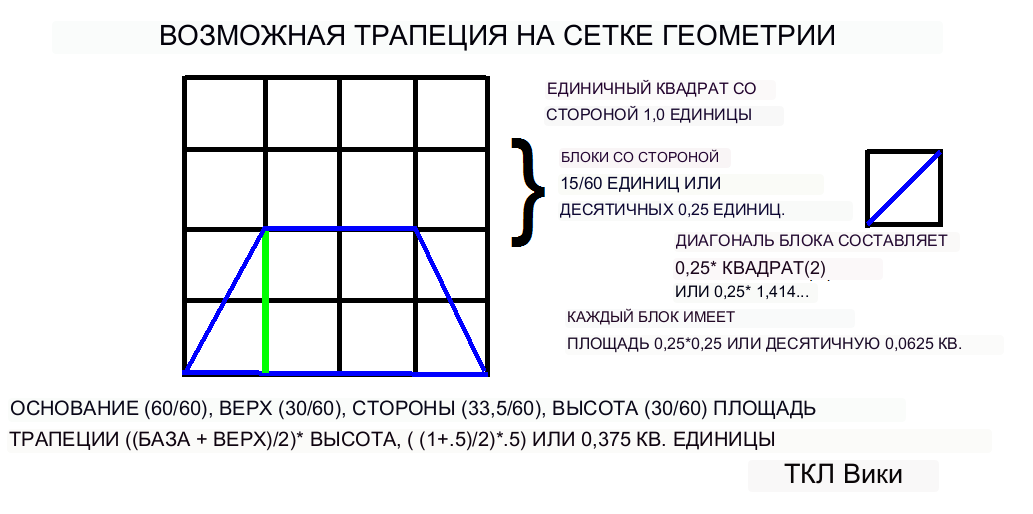
Для кругового сегмента 120 градусов базовая длина равна (120/360)*2*PI*r. Для единичной окружности диаметром 1 и радиусом 0,5 базовая длина равна (120/360)*2*PI*,5 или 1,0471. Длина сегмента или длина тетивы равна эталонной длине, умноженной на шестидесятеричное значение 0;52:30 или десятичное число 0,875. Высота сегмента или ширина тетивы равна (образующий радиус) - (расстояние до хорды), 0,5-0,25 или 0,25. Коэффициент фигуры треугольника или поля зерна равен шестидесятеричному 0;06:33:45 или десятичному 0,1094. Шумерская общая формула площади будет следующей: площадь зернистого поля = коэффициент * поперечное * поперечное или с использованием десятичных дробей 0,1094*1,0471*1,0471 или 0,2166.
Существуют также константы для фигуры баржи, основанной на секторе 90 градусов. Фигура баржи представляет собой двойной сегмент и в некоторых текстах также связана с фигурой семени. В таблицах коэффициентов шумеры указывают шестидесятеричную длину 0;52:30 или (52/60+30/3600) или десятичную 0,875. На глиняных табличках коэффициент фигуры баржи указан в шестидесятеричном виде 0;13:20 (13/60+20/3600) или десятичном 0,2222. Общая шумерская формула площади будет выглядеть следующим образом: площадь баржи = коэффициент * поперечное * поперечное или с использованием десятичных дробей 0,2222*0,875*0,875 или 0,1369 квадратных единиц. Площадь двойного сегмента из тригонометрической формулы, уменьшенная для сегмента 90 градусов, равна 2*((PI*r*r)/4-(r*r/2)), 2*((PI*.5*.5)/ 4-(.5*.5/2)), или 0,142699 квадратных единиц. Калькулятор eTCL рассчитал, что площадь двойного сегмента равна 0,1426 квадратных единиц. Шумерская ошибка для площади баржи будет равна (глиняные константы)/(современный тригон) или 1-0,1369/0,1426, или 3,9 процента ниже. Судя по статье Робинсона, шумеры, судя по всему, использовали приближение Герона для равностороннего треугольника как 1-(w**2)/2, 1-((30/60)**2)/2 или десятичное 0,875. Шумерское превышение или ошибка эталонной длины будет составлять (данная глина)/(современный тригон) или 1-0,875/0,866, или 1,04 процента. Шумерская табличка дает 0;12:30 коэффициент площади баржи 0;12:30 или (12/60+30/3600), или десятичное 0,20833. Находя константу по формуле, константа равна площади баржи / (поперечное * поперечное). Коэффициент баржи пересчитывается в современный триг как 0,20472. Шумерское превышение или ошибка коэффициента баржи будет составлять (данная глина)/(современный тригон) или 1-0,20833/0,20472, или 1,76 процента. 1369/0,1426, или минимум на 3,9%. Судя по статье Робинсона, шумеры, судя по всему, использовали приближение Герона для равностороннего треугольника как 1-(w**2)/2, 1-((30/60)**2)/2 или десятичное 0,875. Шумерское превышение или ошибка эталонной длины будет составлять (данная глина)/(современный тригон) или 1-0,875/0,866, или 1,04 процента. Шумерская табличка дает 0;12:30 коэффициент площади баржи 0;12:30 или (12/60+30/3600), или десятичное 0,20833. Находя константу по формуле, константа равна площади баржи / (поперечное * поперечное). Коэффициент баржи пересчитывается в современный триг как 0,20472. Шумерское превышение или ошибка коэффициента баржи будет составлять (данная глина)/(современный тригон) или 1-0,20833/0,20472, или 1,76 процента. 1369/0,1426, или минимум на 3,9%. Судя по статье Робинсона, шумеры, судя по всему, использовали приближение Герона для равностороннего треугольника как 1-(w**2)/2, 1-((30/60)**2)/2 или десятичное 0,875. Шумерское превышение или ошибка эталонной длины будет составлять (данная глина)/(современный тригон) или 1-0,875/0,866, или 1,04 процента. Шумерская табличка дает 0;12:30 коэффициент площади баржи 0;12:30 или (12/60+30/3600), или десятичное 0,20833. Находя константу по формуле, константа равна площади баржи / (поперечное * поперечное). Коэффициент баржи пересчитывается в современный триг как 0,20472. Шумерское превышение или ошибка коэффициента баржи будет составлять (данная глина)/(современный тригон) или 1-0,20833/0,20472, или 1,76 процента. шумеры, по-видимому, использовали приближение Герона для равностороннего треугольника как 1-(w**2)/2, 1-((30/60)**2)/2 или десятичное 0,875. Шумерское превышение или ошибка эталонной длины будет составлять (данная глина)/(современный тригон) или 1-0,875/0,866, или 1,04 процента. Шумерская табличка дает 0;12:30 коэффициент площади баржи 0;12:30 или (12/60+30/3600), или десятичное 0,20833. Находя константу по формуле, константа равна площади баржи / (поперечное * поперечное). Коэффициент баржи пересчитывается в современный триг как 0,20472. Шумерское превышение или ошибка коэффициента баржи будет составлять (данная глина)/(современный тригон) или 1-0,20833/0,20472, или 1,76 процента. шумеры, по-видимому, использовали приближение Герона для равностороннего треугольника как 1-(w**2)/2, 1-((30/60)**2)/2 или десятичное 0,875. Шумерское превышение или ошибка эталонной длины будет составлять (данная глина)/(современный тригон) или 1-0,875/0,866, или 1,04 процента. Шумерская табличка дает 0;12:30 коэффициент площади баржи 0;12:30 или (12/60+30/3600), или десятичное 0,20833. Находя константу по формуле, константа равна площади баржи / (поперечное * поперечное). Коэффициент баржи пересчитывается в современный триг как 0,20472. Шумерское превышение или ошибка коэффициента баржи будет составлять (данная глина)/(современный тригон) или 1-0,20833/0,20472, или 1,76 процента. или на 1,04 процента выше. Шумерская табличка дает 0;12:30 коэффициент площади баржи 0;12:30 или (12/60+30/3600), или десятичное 0,20833. Находя константу по формуле, константа равна площади баржи / (поперечное * поперечное). Коэффициент баржи пересчитывается в современный триг как 0,20472. Шумерское превышение или ошибка коэффициента баржи будет составлять (данная глина)/(современный тригон) или 1-0,20833/0,20472, или 1,76 процента. или на 1,04 процента выше. Шумерская табличка дает 0;12:30 коэффициент площади баржи 0;12:30 или (12/60+30/3600), или десятичное 0,20833. Находя константу по формуле, константа равна площади баржи / (поперечное * поперечное). Коэффициент баржи пересчитывается в современный триг как 0,20472. Шумерское превышение или ошибка коэффициента баржи будет составлять (данная глина)/(современный тригон) или 1-0,20833/0,20472, или 1,76 процента.
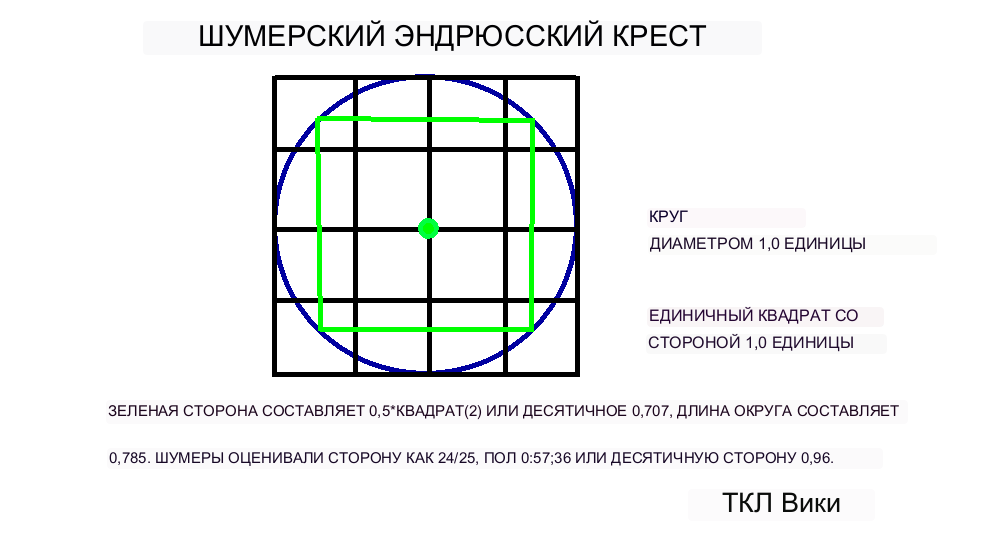
Для сегмента 90 градусов с единичным кругом диаметром 1 и радиусом 0,5 базовая длина равна (1/4)*2*PI*.5 или 0,785. Тетива равна примерно (кв. 2)/2 или 0,7071. Длина тетивы равна эталонной длине, умноженной на шестидесятеричное значение 0;56:40 или десятичное число 0,9444. Ширина тетивы равна эталонной длине, умноженной на шестидесятеричное значение 0;28:20 или 0,4722.
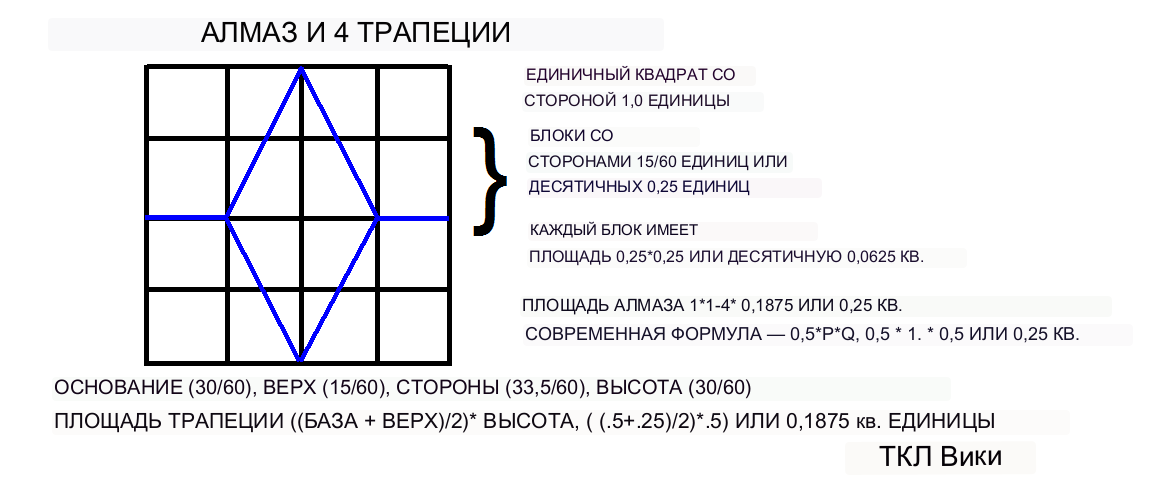
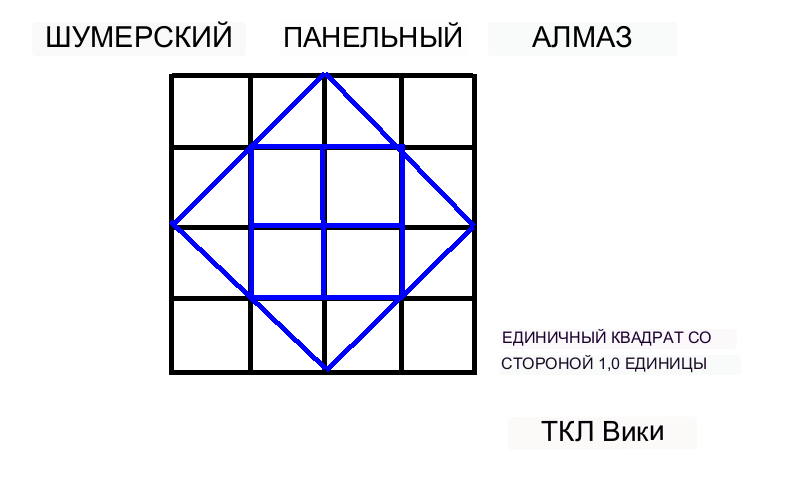
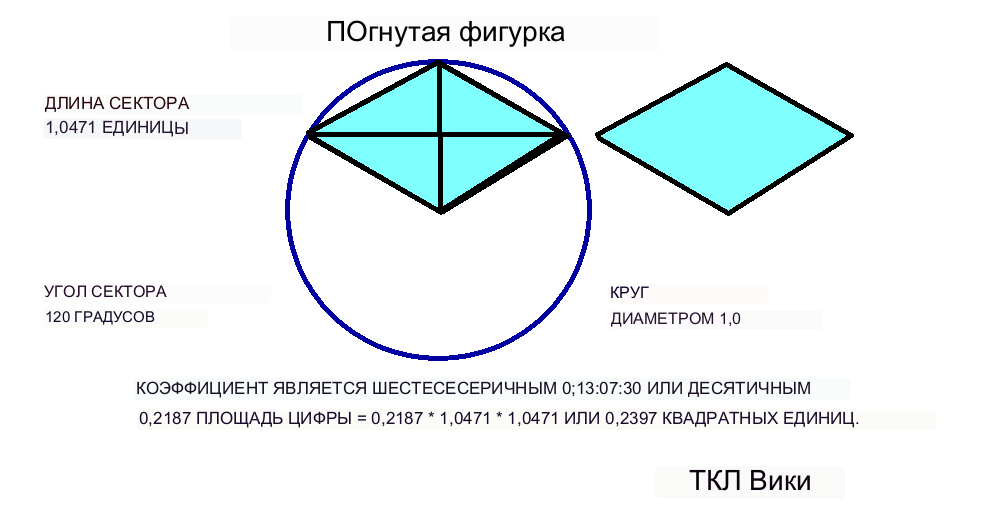
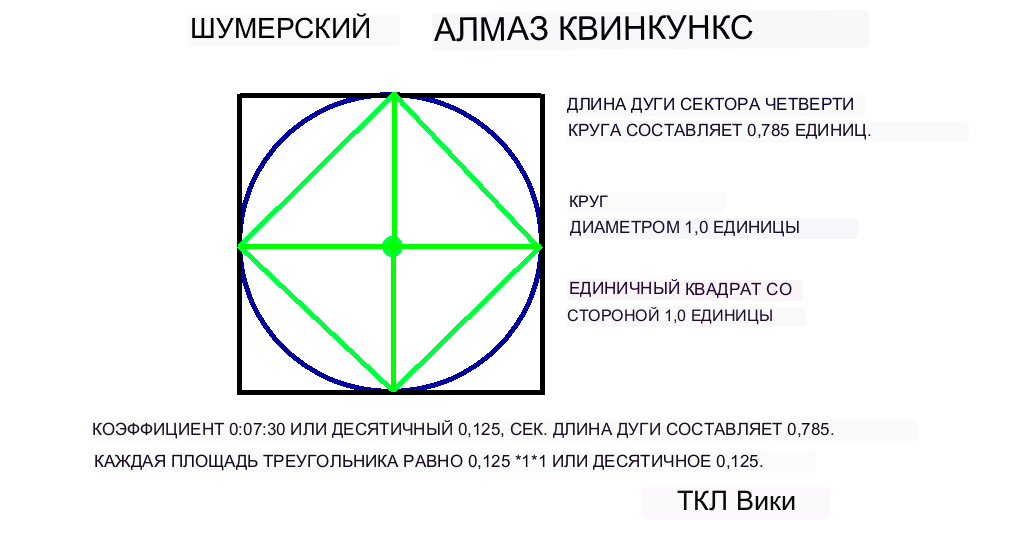
Табличка TMS025 дает метательную палку или ромб площадью шестидесятеричного значения 0;13;07;30 или десятичного значения 0,21874. Коэффициент метания клюшки можно проверить с помощью калькулятора eTCL. Шестидесятеричное число 0;13;07;30 имеет члены 13/60 + 7/3600 + 30/216000, что соответствует точности порядка 30/216000, 3/21600 или 1/7200. В статье Робинсона указывается, что метательная палка или ромбовидная фигура нанесены на сектор круга со стороной 120 градусов. В данном случае площадь ромба равна 0,5* короткое поперечное * длинное поперечное, 0,5*0,5*0,875 или 0,21875. Коэффициент k/(T*T), 0,21875/(0,875*0,875), десятичный 0,28571 или шестидесятеричный 0;17,8,24 (на планшете не найден).
Существуют коэффициенты для второй и третьей фигурок лука. Коэффициент для второго полукруга может быть коэффициентом для четверти круга. Половина фигуры ромба состоит из двух прямосторонних треугольников, рассчитанных выше. Суммарная площадь четырех треугольников 4*((1/2)*((15/60)*(26/60)) или десятичная дробь 0,2166. Решая константу из формулы, константа равна площади ромба / (поперечная *) поперечная) или 0,2166/(0,866*0,866) или 0,2838.
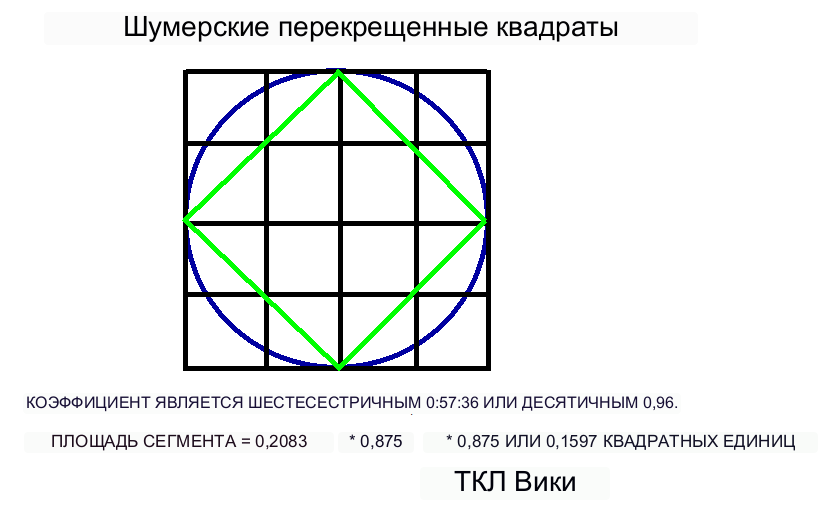
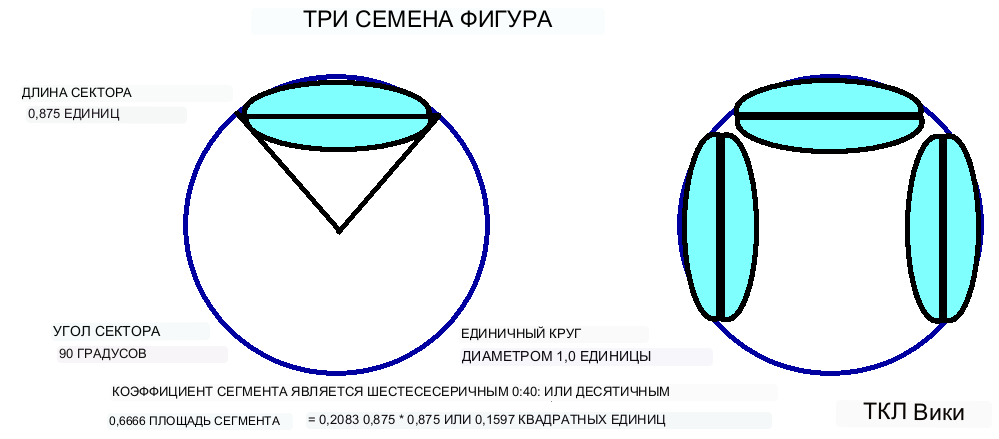
Шумеры использовали круглые сегменты в качестве компонентов других геометрических фигур, называемых фигурами с двумя и тремя семенами. Семя представляло собой два круглых сегмента, соединенных вместе в сетчатом круге, образующих форму семени или боба. Сумма двух семян составила 2*0,1406 или 0,2812 квадратных единиц. Сумма трех семян составила 3*0,1406 или 0,4218 квадратных единиц. В ссылке на табличку был один коэффициент 16/60 для цифры с 2 семенами и строка с пометкой 16 26 46 40 для цифры с 3 семенами. Строку с пометкой 16 26 46 40 было трудно интерпретировать, но, судя по появлению подобных чисел в других строках, это может означать три отдельных числа, например 16/60, (26/60 + 46/3600) и 40/60. Поперечная или эталонная длина будет неизвестна или неопределенна на фигуре с тремя семенами, поскольку существует несколько осей и периметров на выбор. Возможно, эталонная длина будет равна приблизительно квадратному корню из термина (площадь/коэффициент), sqrt(0,2812/0,4461), десятичному 0,793 или шестидесятеричному 0;47:45. Базовая длина исходной фигуры (0,5 * периметр) из сектора 90 градусов составляла 0,785 или шестидесятеричный 0;47:6. Объединенная площадь для трех фигур семян из формулы будет равна площади семян = коэффициент * T * T, 40/60 * 0,785 * 0,785 или 0,4108 квадратных единиц. Ошибка будет равна современной формуле площади/шумерскому уравнению, 1-0,4218/0,4108, или 2,6 процента. 4108 квадратных единиц. Ошибка будет равна современной формуле площади/шумерскому уравнению, 1-0,4218/0,4108, или 2,6 процента. 4108 квадратных единиц. Ошибка будет равна современной формуле площади/шумерскому уравнению, 1-0,4218/0,4108, или 2,6 процента.
Число 16 или 16/60 применяется как к цифрам с 2 семенами, так и к цифрам с 3 семенами. Единицы площади (ган) 0;5:24 (0,09) и 0;45 были указаны из поврежденного текста. Считалось, что 0;45 или 3/4 связаны с площадями четвертей круга или соотношениями четвертей. Площадь одного семени составила 0,1406 или (8/60+26/3600). Уменьшенное соотношение семя плюс круг/площадь круга составляло 2-PI/4, 0;43:36... или десятичное 0,7266.
Раннее предположение при решении шумерских фигурок семян заключалось в том, что все семена должны быть размещены на краю круга, но там могут быть некоторые морщины. Секторы под углом 90 градусов могут содержать до трех семян, размещенных по краю; коэффициенты будут 0,2083 (1 семя), 0,4171 (2 семени), 0,6666 (3 семени), 0,8332 (4 семени) или N *0,2083, 1<=N<=4. Секторы под углом 120 градусов будут содержать до трех семян, размещенных по краю, а именно: 0,2436 (1 семя), 0,4872 (2 семени), 0,7308 (3 семени) или N*0,2436 & 1<=N<=3. Даже несмотря на путаницу или коррозию в некоторых строках коэффициентов, ассоциативный принцип предполагает, что решения представляют собой взаимосвязанные кратные числа. Также следует отметить, что коэффициенты правильно вычисляют площадь семян, даже если семена не расположены на ободе. От планшета BM15285-p40, Обнаружено, что семена меньшего размера (круги меньшего диаметра, чем единичный круг) могут быть помещены внутри единичного квадрата. Кроме того, если учесть, что семена меньшего размера можно размещать внутри квадратов и кругов, семена не обязательно должны размещаться на круглом ободе. Семена с поперечным сечением меньше 0,5 радиуса единичного круга можно разместить в виде розовых лепестков в центре единичного круга. Некоторые конструкции лепестков с 3,4 и т. д. лепестками внутри круга были найдены в таких рисунках, как восьмиконечный символ Иштар. Также возможно, что семена можно разместить рядами или случайным образом внутри круга или квадрата. размещение семян не обязательно должно осуществляться по круглому ободу. Семена с поперечным сечением меньше 0,5 радиуса единичного круга можно разместить в виде розовых лепестков в центре единичного круга. Некоторые конструкции лепестков с 3,4 и т. д. лепестками внутри круга были найдены в таких рисунках, как восьмиконечный символ Иштар. Также возможно, что семена можно разместить рядами или случайным образом внутри круга или квадрата. размещение семян не обязательно должно осуществляться по круглому ободу. Семена с поперечным сечением меньше 0,5 радиуса единичного круга можно разместить в виде розовых лепестков в центре единичного круга. Некоторые конструкции лепестков с 3,4 и т. д. лепестками внутри круга были найдены в таких рисунках, как восьмиконечный символ Иштар. Также возможно, что семена можно разместить рядами или случайным образом внутри круга или квадрата.
Геометрическая фигура «яблочко» представляла собой кольцевую фигуру или фигуру кольца, определяемую внутренним радиусом r1 и внешним радиусом r2, равным 4*r1. Нанесенный на единичный круг диаметром 1 и сетку 15/60 квадратов, внутренний радиус составлял (1/2)*(15/60) или десятичную дробь 0,125. В одной строке глиняного текста указан внешний радиус 0,5. Несколько непоследовательно, в другой строке внешний диаметр яблочка указан как шестидесятеричный 0;53:30 или десятичный 0,875. Диаметр 0;53:30 определялся по круговому сегменту 120 градусов. При соотношении 1:4 площадь внешнего круга была в 16 раз больше площади внутреннего круга. Кроме того, при соотношении 1:4 внешняя площадь составляла 15*пи, или примерно 3*15 или 45 раз больше радиуса внутреннего круга, если использовать шумерское число Пи или 3. Есть некоторые шумерские математические задачи, в которых фигурируют яблочко и цилиндр. были использованы в качестве модели для обжига кирпича. Площадь яблочка, умноженная на высоту печи, использовалась для оценки объема и количества кирпичей внутри кирпичной печи. Площадь внешнего кольца, умноженная на высоту печи, использовалась для оценки объема или количества топлива (древесины или асфальта). При раскопках Иерихона в круглых ямах, которые могли быть печами, были найдены осколки керамики.
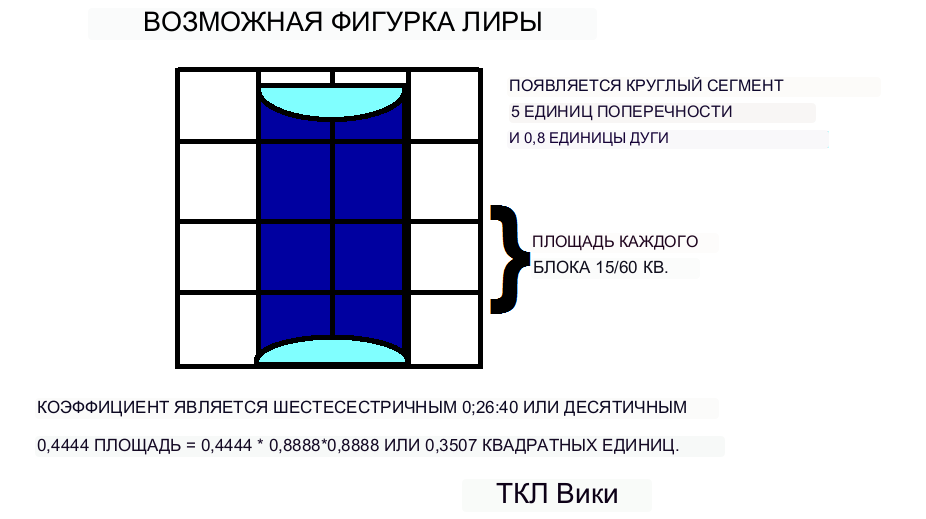
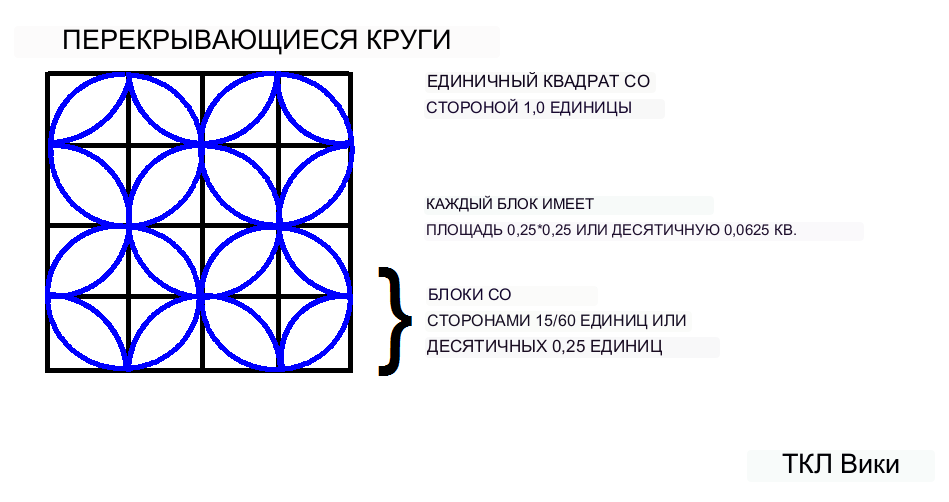
Гис-за-ми (древесный звуковой гимн) или геометрическая фигура лиры была представлена на табличках в виде двух чисел. Коэффициент лиры составлял шестидесятеричный 0;26:40 или десятичный 0,444. Базовая длина или поперечное сечение лиры составляло шестидесятеричную 0:53:20 или десятичную 0,8888. Рядом с фигурой, имеющей вид прямоугольника с двумя вогнутыми дугообразными гранями, была найдена проржавевшая табличка с надписью «гис-за-ми». Предварительный прямоугольник можно разместить и оценить на сетке из 16 квадратов. Шумерская общая формула площади будет следующей: площадь лиры = коэффициент * поперечное * поперечное, = 0,444*0,8888*0,8888, десятичное 0,3507 или шестидесятеричное 0;21:3. Каждый квадрат компонента сетки имеет площадь (15/60)*(15/60) или десятичные 0,0625 квадратных единиц.
Поскольку размеры двух сегментов лука фигуры лиры неизвестны, но невелики, можно разработать определенные утверждения о неравенстве, предполагающие ширину лиры. Ориентировочная площадь лиры будет равна площади прямоугольника минус 2 площади лука, длина * ширина - маленькое неизвестное, 0,8888*0,5 - 2*~ или 0,4444 - 2*~. Если отбросить малые неизвестные для неравенства, то площадь лиры будет меньше 0,4444 квадратных единиц. Для другого аналогичного неравенства площадь прямоугольника минус 2 площади носовой части равняется шумерской формуле: L*W- 2*~ = k*L*L, L*W- 2*~ = 0,444*L*L, L*W =0,444 *L*L + 2*~, тогда W =0,444*L + (2*~)/L. Отбрасывая малые неизвестные для неравенства, W => 0,444*L, W => 0,444*0,8888, W => 0,5 единиц. Поскольку стороны блоков составляют 0,25, а 0,5/0,25 дает 2, W=> 2 блока. Как минимум, ширина лиры должна быть больше, чем площадь/длина, 0,3507/0,8888 или 0. 394 ед. С точки зрения блоков ширина лиры будет больше 0,394/(15/60) или 1,5 блока. Из другого неравенства, поскольку максимальной площадью будет квадрат или L*L, отсюда следует, что k*L*L<=L*L и W*W<=L*L; поэтому W<=L и W<= 0,8/0,25 или 4 блока. Количество квадратов в фигуре лиры будет (площадь лиры)/(площадь блока) 0,3507/0,0625 или примерно 5,6 квадрата. Объединив неравенства, 2. блоков =< W =< 4 блоков. Таким образом, ширина фигуры лиры, вероятно, составляла 0,5 или 2 блока на сетке из 16 квадратов. Количество квадратов в фигуре лиры будет (площадь лиры)/(площадь блока) 0,3507/0,0625 или примерно 5,6 квадрата. Объединив неравенства, 2. блоков =< W =< 4 блоков. Таким образом, ширина фигуры лиры, вероятно, составляла 0,5 или 2 блока на сетке из 16 квадратов. Количество квадратов в фигуре лиры будет (площадь лиры)/(площадь блока) 0,3507/0,0625 или примерно 5,6 квадрата. Объединив неравенства, 2. блоков =< W =< 4 блоков. Таким образом, ширина фигуры лиры, вероятно, составляла 0,5 или 2 блока на сетке из 16 квадратов.
Для сегментов смычка лиры существует несколько возможностей. С помощью калькулятора исследовался набор возможных дуг или дуг. Лук в сегменте 120 градусов имел длину 0,866, ширину 0,25 и площадь 0,0495. Лук в сегменте 90 градусов имел длину 0,7071, ширину 0,1464 и площадь 0,07149. Небольшая дуга в сегменте 132 градуса имела длину 0,458, ширину 0,15, площадь 0,0495 и образующий радиус 0,25. Маленький лук казался лучше всего подходящим для сетки из 16 квадратов.
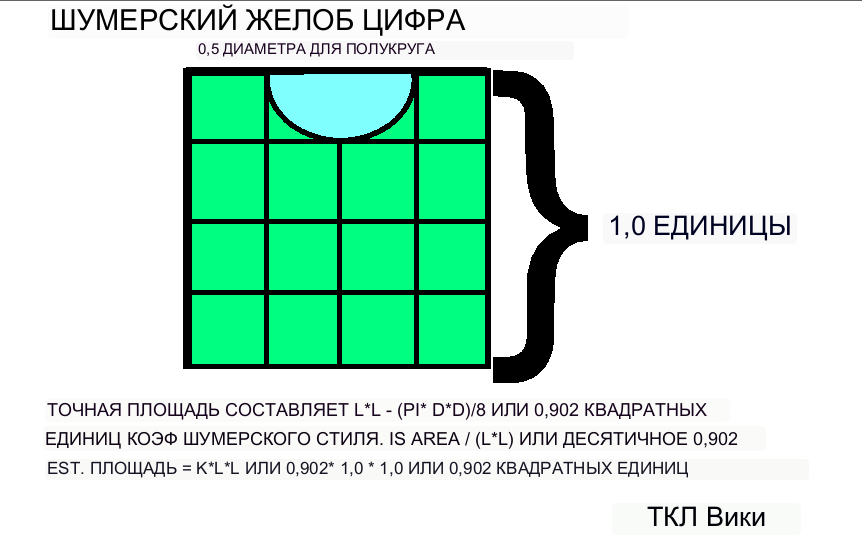
Шумерская фигура корыта имеет некоторое сходство с фигурой лиры, в вершину прямоугольника вставлен лук или полукруг. Здесь доступен только набросок, в качестве примера приведены шумерские методы. Площадь поверхности и коэффициенты площади представляют собой выводы, выходящие за рамки простого эскиза. На основе эскиза фигуру желоба можно смоделировать на сетке из 16 квадратных элементов общей длиной L (например, 1,0). Полукруг имеет диаметр (30/60)*L и достигает (15/60)*L вершины квадрата. Между нижней частью полукруга и основанием квадратной фигуры имеется длина (45/60)*L. Площадь фигуры желоба равна L*L-площадь полукруга, L*L-pi*диаметр*диаметр/8,1*1-pi*.5*.5/8, 1,-0,0982 или десятичные 0,902 квадратных единиц. . Коэффициент площади впадины будет равен площади / (базовая длина * длина), 0,902/(1.*1.) или десятичному 0. 902 кв. ед. Для другого вывода: фигура впадины довольно близка к единичному квадрату со стороной L. Коэффициент площади квадрата будет равен L*L / (базовая длина * длина), (1.*1.)/(1.*1.) , или десятичное 1,0 (см. Фриберг, 1987-90). Существовало несколько видов лир, а также были лиры с квадратными звуковыми коробочками, изображенными на греческих монетах. Полукруг или впадина обеспечивали пальцам лучший доступ к нижней части струн.
Фигура геспана (деревянного лука) внешне похожа на фигуру баржи. На глиняных табличках коэффициент площади деревянного лука указан в шестидесятеричном формате 0;12:30 (12/60+30/3600) или десятичном 0,2083. Ссылочная длина задается в шестидесятеричном формате 0;52;30 или десятичном формате 0,875. Общая шумерская формула площади будет выглядеть следующим образом: площадь деревянного лука = коэффициент * поперечное * поперечное или с использованием десятичных дробей 0,2083 * 0,875 * 0,875 или 0,1595 квадратных единиц (двойной сегмент). Базовая длина 0,875 означает, что фигура гес-пана была получена из сектора 90 градусов. Существует достаточная разница в коэффициенте баржи (0;13:20) и коэффициенте деревянного поддона (0;12:30), чтобы предположить некоторый другой вывод этих терминов. Разница, по-видимому, заключается в том, оценивается ли неизвестная сторона треугольника по теореме Пифагора (результат: 15/60) или по формуле Герона (результат: 26/60 + 25/3600).
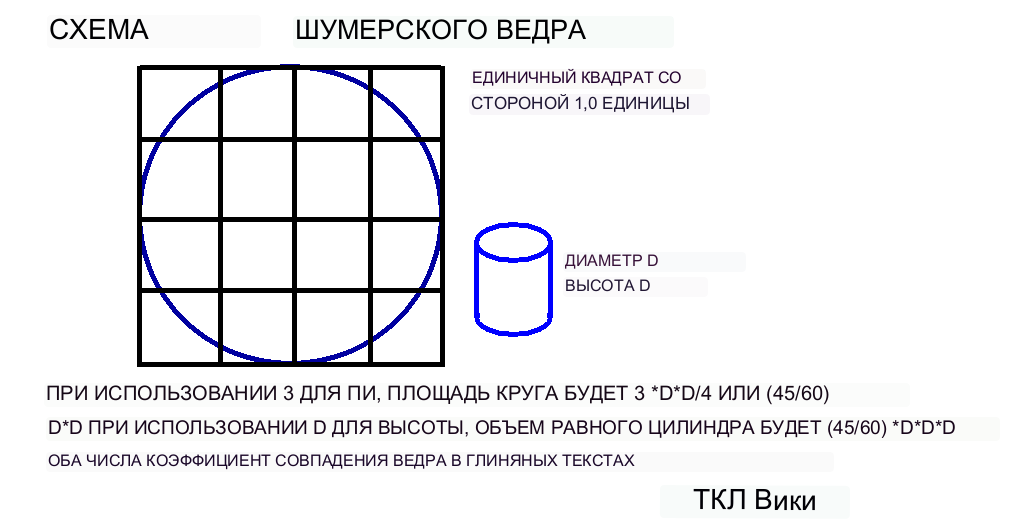
В списке коэффициентов есть коэффициент сегмента 0;45 или десятичный 45/60. Если предположить, что ведро имело диаметр 1 и высоту 1. Используя 3 для числа Пи, объём ведра будет равен (3*диаметр*диаметр/4)*диаметр, (3/4*диаметр в кубе или (45/ 60)*диаметр в кубе. Здесь нужен текст задачи, чтобы узнать, использовалось ли ведро в качестве количества или формулы. В некоторых задачах задание одного человека на удаление почвы составляет 20/60 гар*гар*кус(единица объема) ), но контекст ведер неясен. Силитум или куча земли имеет объем 20/60 сар, что, по-видимому, является рабочим заданием одного человека. Поскольку шумерская нагрузка на ярмо составляла бы 2 таланта или 60 000 граммов в современных единицах измерения, Одно ведро или корзина, вероятно, вмещало не менее 30 000 граммов. Египетский артабе вмещал 37,78 литров, что эквивалентно 30,28 кг пшеницы. Вавилонский пану - 36 литров или 28. 85 кг пшеницы. Если говорить о более конкретных текстах, то шумерское ведро или корзина (dusu,gis-u-sub,pisannu), вероятно, имело объем от 30 до 36 литров, а водный эквивалент - от 30 до 36 килограммов.
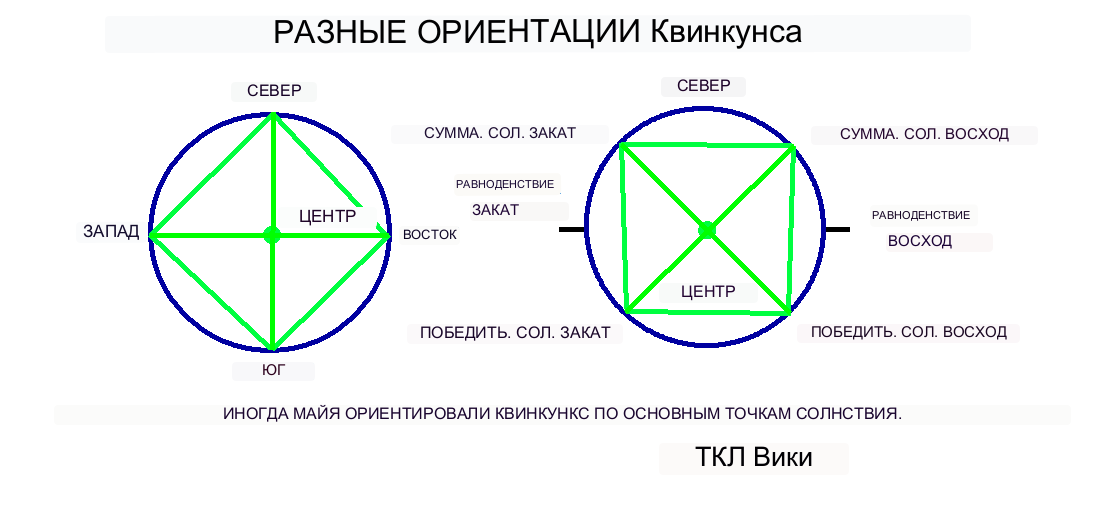
Подразделенный квадрат называется ромбовидным квинконсом, который был известен также у древних китайцев и майя. Квинконс означает 5 частей, считая центр и 4 стороны света. Иногда майя ориентировали квинконс на четыре точки равноденствия(2) и солнцестояния(2). У майя иногда добавлялись 2 солнечные верхние точки или точки пересечения, чтобы включить 7 точек.
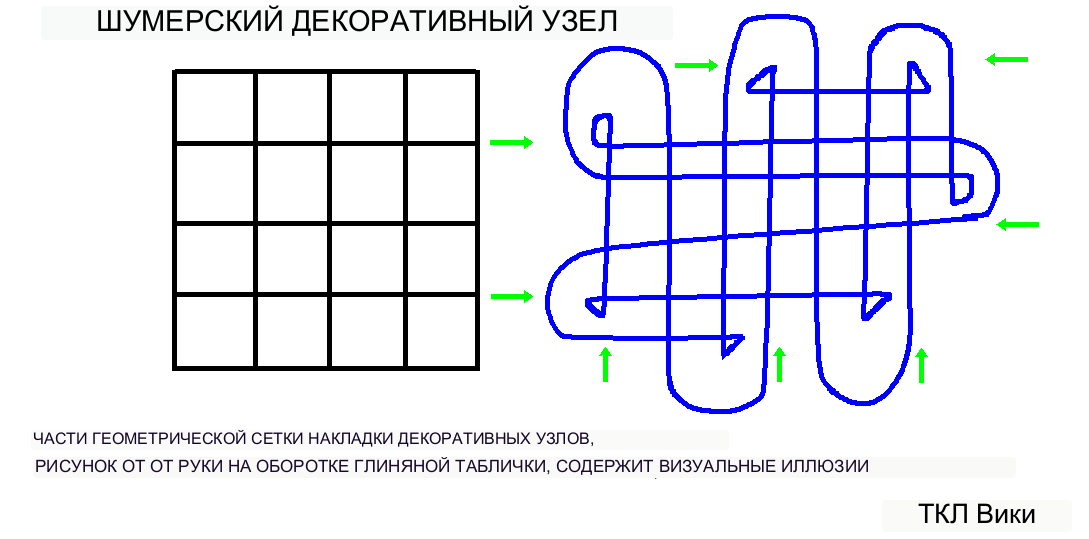
Ключом к пониманию многих шумерских геометрических коэффициентов и фигур является сетка из 16 квадратов с единичным квадратом и единичным кругом. Даже некоторые загадочные фигуры основаны на сетке из 16 квадратов. Сложный узелковый узор был найден на обратной стороне глиняной таблички, возможно, в качестве декоративной обложки книги. Рисунок от руки содержит множество визуальных иллюзий. Некоторые части декоративного узла перекрывают сетку из 16 квадратов, включая прямые линии и повороты веревки.